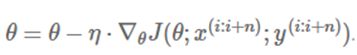TensorFlow 学习（九）：CNN-梯度下降

 

一、介绍

梯度下降是常用的卷积神经网络模型参数求解方法

求参数过程即最小化损失函数过程。比如有一个含有D个训练数据的数据集，损失函数如

下：

下面比较8种梯度下降方法：

批量梯度下降法（Batch Gradient Descent）
随机梯度下降法（Stochastic gradient descent）
小批量梯度下降法（Mini-Batch Gradient Descent）
Nesterov加速梯度法（NAG）
Adagrad法（adaptive gradient，自适应梯度）
Adadelta法
RMSprop 法（均方根传播）
Adam法（自适应性动量估计法）

 

二、方法

批量梯度下降法（Batch Gradient Descent）

是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新。对几百万个样本集，训练时间和内存都不可取。

1、对于给定的迭代次数，首先基于在整个数据集上求出的罚函数J(θ)对输入的参数向量 θ 计算梯度向量。

2、然后对参数θ进行更新：对参数θ减去梯度值乘学习率的值，也就是在反梯度方向，更新参数。当目标函数 J(θ) 是一凸函数时，则批量梯度下降法必然会在全局最小值处收敛；否则，目标函数则可能在局部极小值处收敛。

缺点;

1、每次更新均需要在整个数据集上求出所有的偏导数。因此批量梯度下降法的速度会比较慢。

2、梯度下降法不能以“在线”的形式更新模型，也就是不能在运行中实时加入新的样本进行运算。

随机梯度下降法（Stochastic gradient descent）

由于批量梯度下降法在更新每一个参数时，都需要所有的训练样本，所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法（Stochastic Gradient Descent，简称SGD）正是为了解决批量梯度下降法这一弊端而提出的。

缺点：

SGD 很难在陡谷（在一个方向的弯曲程度远大于其他方向表面弯曲情况）中找到正确更新方向。而这种陡谷（峡谷：深度大于宽度谷坡陡峻的谷地），经常在局部极值中出现。收敛速度变慢

优点：

1、优点1（去冗余）

（1）批量梯度下降法：在每次更新前，会对相似样本求算梯度值，在较大数据集上的计算会有些冗余（redundant）。

（2）随机梯度下降法：通过每次更新仅对一个样本求梯度，去除了这种冗余情况。运行速度被大大加快，同时也能够“在线”学习。

2、优点2

相比批量梯度下降法的收敛会使目标函数落入一个局部极小值，SGD 收敛过程中的波动，会帮助目标函数跳入另一个可能的更小的极小值。

 

 

小批量梯度下降法（Mini-Batch Gradient Descent）

有上述的两种梯度下降法可以看出，其各自均有优缺点，那么能不能在两种方法的性能之间取得一个折衷呢？即，算法的训练过程比较快，而且也要保证最终参数训练的准确率，而这正是小批量梯度下降法设计的初衷。

MBGD在每次更新参数时使用b个样本（b一般为较小的数如100）

小批量梯度下降法集合了批量梯度下降法和SGD的优点，在每次更新中，对 n 个样本构成的一批数据，计算罚函数 J(θ)，并对相应的参数求导：

优点：

1、相比SGD,降低了更新参数的方差（variance），使得收敛过程更为稳定；

2、相比批量梯度下降法，不用对整个数据集求罚函数，可减少计算冗余，加快收敛速度。

3、能够利用最新的深度学习程序库中高度优化的矩阵运算器，高效地求出每小批数据的梯度。通常一小批数据含有的样本数量在 50 至 256 之间，但对于不同的用途也会有所变化。

4、小批量梯度下降法，通常是训练神经网络的首选算法。

Nesterov加速梯度法（NAG）

基本思想：既然每一步都要将两个梯度方向（历史梯度、当前梯度）做一个合并再下降，那为什么不先按照历史梯度往前走一小步，按照前面一小步位置的“超前梯度”来做梯度合并呢？如此一来，小球就可以先往前走一步，在靠前一点的位置看到梯度，然后按照那个位置再来修正这一步的梯度方向。如此一来，有了超前的眼光，小球就会更加“聪明” 。

公式描述：使用动量项γvt-1 来“移动” 参数项θt

优点：

通过基于未来参数的近似值而非当前的参数值计算相应罚函数 J(θt-γvt-1) 并求偏导数，能让优化器高效地“前进”并收敛。

这种基于预测的更新方法，可避免过快地前进，提高了算法响应能力。

Adagrad法（adaptive gradient，自适应梯度）

缺点：

1、学习率是单调递减的，训练后期学习率非常小。这会导致网络更新能力越来越弱，能学到更多知识的能力也越来越弱，并最终gradient→0，使得训练提前结束。

2、更新时，左右两边单位不一致的问题。

3、仍依赖于人工设置一个全局学习率η。

优点：

AdaGrad可以自动变更学习速率：设定一个全局学习率η ，每次迭代时自动更新学习率η : 对迭代次数 t，基于每个参数之前计算的梯度值，将每个参数的学习率η按如下方式修正

1、每次迭代，能够实现学习率自动更新，即学习率会根据历史梯度的变化而变化。

2、大梯度对应小的学习率，小梯度对应大的学习率。从而加快收敛。

Adadelta法

Adadelta 法是Adagrad 法的一个延伸，它旨在解决Adagrad以上三个问题。

相较于Adagrad法，更优

RMSprop 法（均方根传播）

RMSprop法（Root Mean Square prop）和Adadelta法几乎同时被发展出来，是AdaGrad算法的改进，在非凸条件下结果更好。

缺点：

依然依赖于全局学习率；

优点：

1、RMSprop算是Adagrad一种发展：很好解决了深度学习过早结束问题（梯度从1到t时刻累加，随着时间增加，学习率单调递减，训练后期学习率非常小。导致网络更新能力越来越弱，使得训练提前结束）。

2、适合处理非平稳目标。- 对于RNN效果很好。

Adam法（自适应性动量估计法）

自适应性动量估计法（Adam，Adaptive Moment Estimation）是另一种能对不同参数计算适应性学习率的方法。

Adam法：本质上是带有动量项的RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。

优点:

Adam 也是基于梯度下降的方法，但每次迭代参数的学习步长都有一个确定范围，不会因为很大的梯度导致很大的学习步长，参数的值比较稳定。