论文笔记19 --（ReID）Orthogonal Center Learning with Subspace Masking for Person Re-Identification

《Orthogonal Center Learning with Subspace Masking for Person Re-Identification 》
论文：https://arxiv.org/abs/1908.10535

这是Tencent Youtu X-lab的一篇，子空间掩蔽正交中心学习。

---

Abstract

文章提出了一种新的基于子空间掩膜的正交中心学习方法，用于行人重识别。有以下贡献：
（1）构建了中心学习模块，通过正交化同时减少类内差异和类间相关性来学习类别中心；
（2）引入子空间掩蔽机制，来增强学习的类中心的泛化性；
（3）设计以一种规则化的方式整合avg pooling和max pooling，以充分利用其能力。

1. Introduction

对图像进行行人重识别的任务是在不同的拍摄环境（例如摄像机视角，人物姿势和照明条件）中识别同一个人。它广泛应用于监视、行人跟踪或可能涉及大量行人的其他场景。因此，需要鲁棒的行人重识别算法来应对大量行人类别。

目前行人重识别方法有着重于改进特征学习模块的结构，或设计更有效的损失函数，本文所做工作正是这件事情。设计损失函数的一种典型方法是将softmax损失和triplet损失结合在一起，因为它们的优势是互补的：softmax损失将优化定义为分类问题，并尝试正确地对每个样本进行分类，而triplet损失旨在最大程度地增加不同类两个样本之间的相对距离。

有一个损失函数center loss，其目的是使同类样本间的距离最小。它最初被提出用于人脸识别，但也可以直接应用于Re-ID。在这篇论文中，作者提出了一种新的正交中心学习模块，以进一步增强特征学习过程。与center loss不同，作者不仅通过最小化每个样本到其对应中心的距离，而且还通过最大化不同类别样本之间的可分离性来制定学习目标函数。具体来说，就是利用正交化来减少类间相关性。

接下来讲了些正交正则化的研究应用史，比如通过缓解递归神经网络（RNN）中的梯度消失/爆炸，正交正则化已广泛用于改善性能和训练效率。还有用于减少学习的特征之间的相关性。作者表示受此启发，他们使用正交化来对类别中心进行解相关，从而可能在不同类别的样本之间产生更好的可分离性。此外，正交正则化还促进充分利用类别中心的嵌入空（embedding space）间。

为了进一步提高类别中心的通用性并释放其全部潜力，作者在中心学习模块中提出了子空间掩蔽机制。具体来说，会随机掩蔽中心嵌入的某些单元以使其失效，并在训练过程中与其余激活单元一起学习中心。因此，这种掩蔽机制促进类别中心在其子空间中具有代表性，从而测试时在整个空间中产生更具通用性的类别中心。

提出的中心学习模块与softmax loss和triplet loss一起工作，并且可以端到端的训练整个模型。在实践中，对类中心进行参数化，以使它们参与整个模型的优化，这与classical center loss相反：交替更新类中心并优化模型参数。为了降低计算复杂度并减轻潜在的过拟合，通常在卷积网络的最后一层应用平均或最大池化，两种池化有各有优点。作者设计一种分步学习方案的正则化方法，整合这两种池化方法，以探索它们的组合潜力。

总而言之，本文提出的方法具有以下优点：

• 提出了一个中心学习模块，该模块通过两种策略学习类中心：最小化类内距离，以及通过使用正交化降低类间相关性来最大化类间可分离性。
• 提出了一种子空间掩蔽机制来改善类中心的泛化。
• 设计了一种规范化的方法来整合平均池化和最大池化，以充分释放它们的组合能力。

2. Related Work

关于行人重新识别的工作很多。下面，作者回顾了与文章提出的方法密切相关的最具代表性的方法。大多数人的Re-ID方法遵循两方面的研究：特征提取和度量学习（feature extraction and metric learning）。

Feature extraction 特征提取。 传统方法通常设计出手工制作的特征，这些特征对视视点和遮挡是不变的。随着深度神经网络的巨大成功及其强大的表示能力，基于CNN的许多新的Re-ID方法得到了发展。

特别是，有人最近引入了细粒度的部件信息来改进特征表示。有人使用高级姿势估计和语义分割。还有工具可显式预测关键点或隐式定位可区分的局部区域。除了使用现有的姿势估计器外，注意力机制在那些利用辨别性局部信息时变得很流行。还有HA-CNN（harmonious attention CNN），该方法可以同时学习soft pixel attention 和 hard regional attention并同时优化特征表示。还有人提出了MLFN，将人的视觉外观分解为多个语义层次的潜在辨别因素，而无需人工标注。还有将特征图分成几个水平部分，并对其进行监督，以学习零部件级特征。有人将每个分区中的平均池化和最大池化直接结合起来，以利用全局和本地信息。然而，将平均池化和最大池化操作直接融合到同一个特性映射上并不能充分利用这两种池化方法的优点。为了解决这一局限性，我们提出了一种整合这两种池化的正则化方法。

Metric learning 度量学习。 度量学习方法旨在扩大类间差异，同时减少类内差异，这为验证和识别任务提供了天然的解决方案。关于Re-ID的代表性工作包括softmax classification loss，contrastive loss，triplet loss，quadruplet loss，re-ranking。

Center loss是近年来提出的一种促进类内紧凑性的方法，在人脸识别和person Re-ID方面取得了很好的效果，它在一个mini-batch内为每个类学习一个中心，同时惩罚深层特征与其类中心之间的欧几里德距离。最近，基于softmax loss，已提出了几种multiplicative angular margin-based的方法来增强深度特征的判别能力。与经典的center loss不同，通过正交化，我作者不仅最小化了每个样本到其对应中心的距离，而且最大化了不同类别样本之间的可分性，减少了类间相关性。与在triplet loss上进行instance-level 全局正交正则化将负对推至正交（在特征空间中）不同，文章方法是在不同类中心之间执行正交正则化以减少类间相关性。此外，还引入子空间掩蔽机制来改善子空间中类中心的泛化。与在特征空间中执行删除操作的Dropout不同，作者提出的子空间掩蔽机制在中心嵌入空间中执行掩蔽，以提高学习类中心的泛化能力。我们还探索了不同于其他不同于Dropout中通常采用的伯努利分布的其他采样策略，以证明所提出的子空间掩蔽机制的有效性。

3. Method

这篇文章旨在优化特征学习，以使类内样本之间的距离最小化，同时最大程度地提高类间样本之间的可分离性。为此，通过鼓励每个样本靠近相应的类别中心，同时减少类别中心之间的相关性来学习每个类别的中心。此外，提出了一种子空间掩蔽机制，以改善子空间中类中心的泛化。

图1是模型结构。采用softmax loss 和 triplet loss作为基础损失函数来指导特征学习模块（ConvNet C）的优化，这已在Person Re-ID中被证明是有效的。作者提出中心学习模块，以进一步提高基础损失的优化能力。

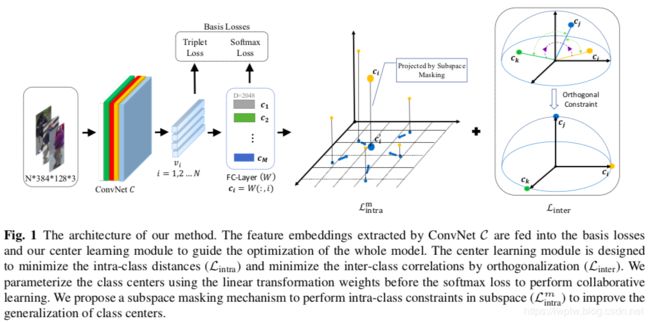
3.1 Center Learning

backbone还是ResNet-50，先提特征，出来后的特征送入中心学习模块和两个损失函数。

Collaborative center learning with softmax loss.
在特征空间中，一个学习良好的类中心被用来描述属于这个类的样本。直观地说，在特征空间中，一个优化中心可以作为该类样本的几何中心，但这是不可行的，因为样本特征和类中心是相互依赖地进行优化的。有一种折衷的方法是随机采样一个中心位置，然后使用近似中心位置迭代更新，该近似中心位置被计算为每个训练批次中属于该类的样本特征的几何中心。因此，样本特征和类中心交替进行优化。该过程的潜在缺陷是类中心不直接参与特征学习（ConvNet C）的梯度下降优化，因而优化效率低且不稳定。为了解决这一问题，作者提出对类别中心进行参数化，并与ConvNet C一起进行优化。
具体来说，我们将类别中心与softmax函数之前的线性变换的参数$W\in {\mathbb{R}}^{d\times M}$对应，该函数将特征映射（feature embeddings）从$d$投射到$M$（类别数）。 $W$的每一列都设置了一个相应的类别中心：
等式（1）：
$c_i=W(:,i)$
其中$W(:,i)$表示$W$的第$i$列。此设计的基本原理是，可以将变换矩阵$W$的每一列视为一个类embedding，以通过点积衡量该类与样本feature embedding之间的兼容性。因此，这符合我们中心学习的意图，类别中心$C=（c_1,c_2,...,c_M）:=W$可以通过中心学习模块和softmax损失进行协作优化。
在中心学习模块中，我们采取了两管齐下的策略来指导类中心$C$的优化：最大程度地减少类内距离并减少类间的相关性。

Minimizing intra-class distances.
考虑一次训练迭代中的一批样本${\left\{v\right\}}_{i=1}^B$，我们将每个样本与其对应的类别中心之间的欧式距离之和最小化：
等式（2）：
${\mathcal{L}}_{intra}={\sum }_{i=1}^B{\Vert v_i-c_{y_i}\Vert }^2$

Reducing inter-class correlations by orthogonalization.
应用正交化来减少类中心之间的相关性，从而增加不同类样本之间的可分离性。具体来说，我们首先通过L2-norm对每个类别中心进行归一化，然后在中心学习模块中采用根据标准Frobenius norm执行的软正交约束：
等式（3）:
$c_i=\frac{c_i}{\Vert c_i\Vert },i=1,...,M$
${\mathcal{L}}_{inter}=\lambda {\Vert C^{\top }C-I\Vert }_F^2$

由于等式3的优化与输入样本无关，因此易于迅速收敛到较差的局部最优值。为了使优化过程更加平滑并与其他损失函数的优化同步，作者仅将正交约束应用于每个迭代的当前训练批次中涉及的（样本）类中心。

从理论上讲，上等式（3）中正交约束有潜在缺陷，当类别的数量显著大于中心embeddings的尺寸（$M\gg d$）时，所有中心都不能严格彼此正交。在这种情况下，Bansal等人（2018）的一个可行解决方案是放宽约束以最小化任何一对中心之间的最大相关性，这等效于最小化：
等式（4）:
${{\mathcal{L}}^{\prime }}_{inter}=\lambda {\Vert C^{\top }C-I\Vert }_{\infty }$

在实践中，发现等式（3）中的标准正交损耗Linter足以满足实验中使用的实际数据集的要求，因为我们的目的是减少类间相关性，而不是严格遵循中心之间的正交化。

增加类中心之间可分离性的另一种方法是通过Hinge loss直接最大化成对的欧几里得（Euclidean）距离：
等式（5）:
${\mathcal{L}}_{inter-euclid}={\sum }_{i=1}^B{\sum }_{j=1j\ne 1}^{B}max(0,m-\Vert c_{y_i}-c_{y_j}\Vert )$

它与公式（3）中基于正交化的loss之间的差异在于，${\mathcal{L}}_{inter-euclid}$在欧几里得空间中执行约束，而正交化在角度空间中进行操作以减少类间相关性，各自都有其优点。 然而，由于我们采用triplet loss作为基本loss，并且在欧几里得空间中也执行类间约束，因此作者认为${\mathcal{L}}_{inter-euclid}$不是必需的，后续实验证实了该推测。

3.2 Subspace Masking

作者在中心学习模块中提出了一种子空间掩蔽机制，以改善类中心的泛化并释放其全部潜力。关键思想是根据概率将center embeddings的某些单元掩蔽，以使它们无效，而在训练过程中将其余单元激活。因此，能够增强类中心在子空间中的表示能力。尤其是，对于center embeddings的每个单元，使用其在类内损失${\mathcal{L}}_{intra}$上遵循伯努利分布$B(p)$的概率对其进行掩蔽：
等式（6）：
${\mathcal{L}}_{intra}^m={\sum }_{i=1}^B{\sum }_{k=1}^{d}B(p){\Vert v_i^k-c_{y_j}^k\Vert }^2$

其中$d$是center embeddings的大小（以及feature embeddings $v_i$），$p$是从伯努利分布中采样值为1的概率。实际上，作者将其作为超参数进行处理，并根据保留的验证集选择其值。

子空间掩蔽机制的好处有三方面：

• 中心学习的观点：子空间掩蔽鼓励类中心在物理上代表其在子空间中的相应类。由于可以在不同的训练迭代中随机选择不同的子空间，因此类中心可以在测试时对原始完整空间进行更好的概括。
• 特征学习的视角：子空间掩蔽机制还指导特征学习在子空间中具有区分性。它鼓励模型捕获local patches中的潜在区分特征。