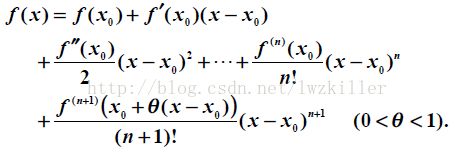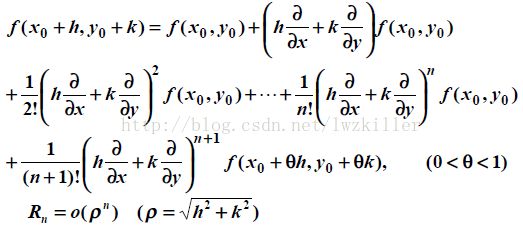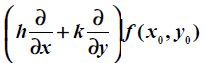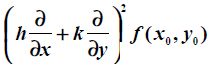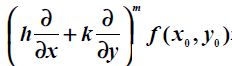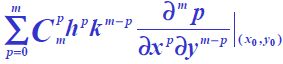Hessian矩阵以及在图像中的应用
Hessian Matrix,它有着广泛的应用,如在牛顿方法、求极值以及边缘检测、消除边缘响应等方面的应用。一个Hessian Matrix涉及到很多数学相关的知识点,比如泰勒公式、极值判断、矩阵特征值及特征向量、二次型等。本篇文章,主要说明多元情况下的极值判定、hessian矩阵与二次型的联系以及有关hessian matrix在图像上的应用。
1. 二元函数泰勒公式
对于一元函数的泰勒公式,大家都有所了解,其意义是使用多次多项式来近似表达原函数f(x),一元函数的f(x)的泰勒公式如下:
在实际应用中,我们一般取前面几阶多项式的和来近似表达原函数f(x)。
然而,在图像处理中,我们应用的都是二元函数f(x,y),下面着重讲解下二元函数的泰勒公式:
如果![]() 在点
在点![]() 的某一邻域内连续且有到n+1阶的连续偏导数,
的某一邻域内连续且有到n+1阶的连续偏导数,![]() 为此邻域的任意一点,则有
为此邻域的任意一点,则有
人生苦短,关于这些公式这里就不证明了,大家可以参考相关数学资料进行证明。
2. 极值判断
如果对于函数中某一点其一阶导数为0,二阶导数不为0,那么该点必定为极值点。再进一步分析,如果二阶导数大于0,那么该点为极小值点,如果二阶导数小于0,那么该点为极大值点。关于这些性质的描述,最直观方法就是自己画图进行理解。另外可以通过表达式给予一些直观理解(省略后面的多阶余项),虽然表达式并非严格,比如,对于一元函数进行泰勒公式展开并认定完全相等:![]()
针对凸函数,如果在x0处的一阶为0,二阶为正,那么我们就可以断定f(x)肯定比在x0处的函数值大,我们可以认为x0为极小值点。对于图像中的二元函数呢?我们是可以类推的。根据上述二元泰勒公式可得二阶近似表达式:
![]() ,对于二元函数极值情形,我们可以根据二阶表达式的正负进行判定。
,对于二元函数极值情形,我们可以根据二阶表达式的正负进行判定。
对于这种情形,这里面会涉及到Hessian矩阵正定以及负定的判断,这里令![]() ,
,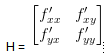 ,如果对于任意向量
,如果对于任意向量![]() ,都有
,都有![]() 为正,那么
为正,那么![]() 有最小值,且H为正定的。如果对于任意向量
有最小值,且H为正定的。如果对于任意向量![]() ,都有
,都有![]() 非负,那么
非负,那么![]() 有最大值,且H为负定的。
有最大值,且H为负定的。
3. 二次型的性质
可以发现上面矩阵H即为Hessian矩阵,具有对称性。而二次型的矩阵也是对称的,接下来主要介绍下二次型最优化,以一个具体例子进行说明。
最小化二次型函数![]() ,其中A是实对称二阶矩阵,即是hessian矩阵,
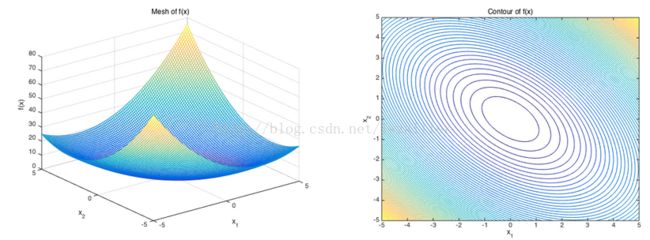
,其中A是实对称二阶矩阵,即是hessian矩阵,![]() ,对于该问题的优化很简单,最终该问题的结果与矩阵A的特征值相关。我们可以绘制二次型函数以及对应的等高线如下:
,对于该问题的优化很简单,最终该问题的结果与矩阵A的特征值相关。我们可以绘制二次型函数以及对应的等高线如下:
并且我们求得矩阵A的特征向量[-0.7071,0.7071],[0.7071,0.7071],对应的特征值分别为0.5,1.5
我们可以知道等高线越密集的地方,说明函数值变化较快,而这个函数变化最快的方向即是特征向量[0.7071,0.7071]所对应的方向;等高线越稀疏的地方,说明函数值变化较慢,而变化最慢的方向即是特征向量[-0.7071,0.7071]所对应的方向,并且可以观察矩阵特征值的大小与函数值变化程度有关,较大特征值所对应的特征向量方向上的函数值变化最快,较小特征值所对应的特征向量方向上的函数值变化最慢。
这里描述二次型的目的就是讲解Hessian矩阵的特征值以及特征向量与二次型函数值变化之间的关系。其中二次型函数的二阶偏导就构成了Hessian矩阵,也即是A矩阵。
4. 边缘检测以及边缘响应消除
既然检测到的对应点确认为边缘点,那么我们就有理由消除这个边缘点,所以边缘检测与边缘响应消除的应用是一回事。边缘到底有什么特征呢?如下图所示,一个二维平面上的一条直线,图像的特征具体可以描述为:沿着直线方向,亮度变化极小,垂直于直线方向,亮度由暗变亮,再由亮变暗,沿着这个方向,亮度变化很大。我们可以将边缘图像分布特征与二次型函数图形进行类比,是不是发现很相似,我们可以找到两个方向,一个方向图像梯度变化最慢,另一个方向图像梯度变化最快。那么图像中的边缘特征就与二次型函数的图像对应起来了,其实二次型函数中的hessian矩阵,也是通过对二次型函数进行二阶偏导得到的(可以自己求偏导测试下),这就是我们为什么可以使用hessian矩阵来对边缘进行检测以及进行边缘响应消除,我想大家应该明白其中的缘由了。还是那句话,数学模型其实就是一种反映图像特征的模型。
所以Hessian matrix实际上就是多变量情形下的二阶导数,他描述了各方向上灰度梯度变化,这句话应该很好理解了吧。我们在使用对应点的hessian矩阵求取的特征向量以及对应的特征值,较大特征值所对应的特征向量是垂直于直线的,较小特征值对应的特征向量是沿着直线方向的。对于SIFT算法中的边缘响应的消除可以根据hessian矩阵进行判定。
关于hessian的应用基本讲完了,有问题可以留言讨论。
参考文献:
1.https://www.zhihu.com/question/40181086
2.https://zh.wikipedia.org/wiki/%E6%B5%B7%E6%A3%AE%E7%9F%A9%E9%98%B5
3.http://www.zhihujingxuan.com/18143.html
4.http://blog.sina.cn/dpool/blog/s/blog_5d2990b70101c1pc.html
5.http://blog.sina.com.cn/s/blog_790bb71901015087.html
6.http://painterlin.com/2015/09/12/Intuition-of-Eigen-Value.html