python 标准库：numpy使用一

从经典的101个numpy练习中总结：

1、numpy：

python拓展包，可以用于处理大型矩阵，有足够的函数库以及线性转换函数，有许多高级的数值运算工具：

import numpy as np
print(np.__version__)

2、基础操作：

numpy数组类是numpy.array

其中有array.nidm矩阵的维度和，array.size:元素个数，array.dtype元素的类型，array.shape:数组大小,array.itemsize:每个元素字节的大小

创建矩阵：

创建一定范围的一维矩阵：arr=np.arange(10),用法类似range(),有三个参数，第一个是起点第二个是终点，第三个是步长

查询数据类型：array.dtype；转换数据类型：array.astype();查询维度：.ndim;查询元素个数：.size

返回array类型等差矩阵，np.arange(1,10,2)。注意在步长是浮点数的时候，由于arange是有一定误差的所以会产生累计，故使用linspace更好               

np.logspace(1,4,4,base=2,endpoint=True)：生成一个等比数列。

还有一种创建一维矩阵的函数np.repeat(a,b)：将a元素重复b次的一维数组；注意a本身也可以是一个数组：

a = np.array([1,2,3])`

np.r_[np.repeat(a, 3), np.tile(a, 3)]
#> array([1, 1, 1, 2, 2, 2, 3, 3, 3, 1, 2, 3, 1, 2, 3, 1, 2, 3])

创建一定维度的矩阵：np.full((2,3),5)     其中创建布尔值矩阵的方法是：np.full((2,3),Ture,dtype=bool)；或者是np.ones((2,3),dtype=bool)；

其中np.ones()创建全为1的矩阵，np.zero()创建全为零的矩阵,np.empty()可以创建一个初始值受内存状态影响的数组，np.eye()可以输出单位阵，np.random.random()可以输出任意大小元素的矩阵。注意这些元素类型均为float64

numpy.array()的基本运算以及生成函数：

7.np.array 的数组切片
a.切片规则 [三冒号规则]
  [开始：结尾：步长]
b.开始为-1
  a[-1] 取最后一个
  a = [0,1,2,3,4,5,6,7]
  a[-1] = 7
c.结尾为-1（开始必须为大于等于0的数）
  a[2:-1] = [2,3,4,5,6]
d.步长为-1，意味着反转

  a[::-1]=[7,6,5,4,3,2,1]

  

2、numpy打印方式：

np.set_printoptions(precision=3)就是设置输出格式是三位小数

实现输出将科学记数法变为几位小数：np.set_printoptions(suppress=True, precision=6)

设置输出范围：np.set_printoptions(threshold=6):只输出前后的六个元素；np.set_printoptions(threshold=np.nan):全部输出

a[:]打印全部，a[:b]打印到b的元素，a[b:]打印从b开始的元素

注意，np.array.reshape()可以将arange矩阵大小reshap：

numpy库函数：reshape（）的参数：reshape（a，newshape,order='C'）

a:array_like;newshape:新形成的数组的维度必须与之前的兼容，而且不能改变原有的元素值，维度可以是-1；order={‘A’,'C','F'}，控制索引方式；

注意：通过reshape生成的新数组和原始数组公用一个内存，也就是说，假如更改一个数组的元素，另一个数组也将发生改变

特别注意：数组新的shape属性应该要与原来的配套，如果等于-1的话，那么Numpy会根据剩下的维度计算出数组的另外一个shape属性值。

 举几个例子或许就清楚了，有一个数组z，它的shape属性是(4, 4)

z = np.array([[1, 2, 3, 4],
          [5, 6, 7, 8],
          [9, 10, 11, 12],
          [13, 14, 15, 16]])
z.shape
(4, 4)

z.reshape(-1)
array([ 1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16])
#z.reshape(-1, 1)也就是说，先前我们不知道z的shape属性是多少，但是想让z变成只有一列，行数不知道多少，通过`z.reshape(-1,1)`，Numpy自动计算出有12行，新的数组shape属性为(16, 1)，与原来的(4, 4)配套。z.reshape(-1,1)
array([[ 1],
        [ 2],
        [ 3],
        [ 4],
        [ 5],
        [ 6],
        [ 7],
        [ 8],
        [ 9],
        [10],
        [11],
        [12],
        [13],
        [14],
        [15],
        [16]])
 
#z.reshape(-1, 2)newshape等于-1，列数等于2，行数未知，reshape后的shape等于(8, 2)
z.reshape(-1, 2)
array([[ 1,  2],
        [ 3,  4],
        [ 5,  6],
        [ 7,  8],
        [ 9, 10],
        [11, 12],
        [13, 14],
        [15, 16]])

即只要给定newshape=-1,numpy就会根据数组元素数目和提供的行数与列数（如果没有默认是一行）去判断reshape的行数与列数。

3、运算:数组的算数运算适用于元素方式，即运算执行在每个元素上：不同于其他矩阵运算，在numpy数组中，*乘法运算符操作与每个元素。而矩阵的乘积可以使用dot函数或dot方法运行：如+=、*=等操作符，在操作执行的地方替代数组元素而不是产生新的数组 。

若运算的数组时不同的数据型,则遵循向上转型，即结果数组的元素类型为更一般或更精确的数据类型：

>>> a = np.ones(3, dtype=np.int32)
>>> b = np.linspace(0,pi,3)
>>> b.dtype.name
'float64'
>>> c = a+b
>>> c
array([ 1.        ,  2.57079633,  4.14159265])
>>> c.dtype.name
'float64'

4、数组运算、添加以及判断常用函数：

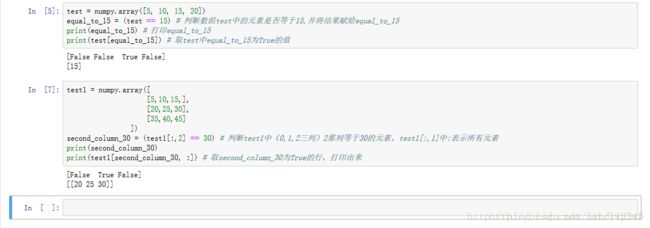
arr[arr%2==1]=-1；

np.where( , x,y)；第一个参数是判断条件，第二个是条件为True的输出值，第三个是条件为False的输出值：np.where不会覆盖原有的数组；np。where返回一个元素是int64的数组，代表原数组的满足条件的元素的index，可以直接通过a[index]引用。

 

np.concatenate([a, b], axis=0)：将a、b两个数组相拼接，axis是轴属性，0是列拼接，1是行拼接，必须有相应相等的行与列；

也可以用 np.vstack([a,b])与np.r_[a,b]进行列拼接;np.hstack([a,b])与np.c_[a,b]进行行拼接。用np.hsplit(a, 3) 和 np.hsplit(a, (3, 4))等方法进行列分割；用 np.vsplit(a, 3) 和 np.vsplit(a, (3, 4))进行行分割

np.setdiff1d(a,b):从a中去除b中存在的元素；

np.logical_and(a>=5, a<=10)：在numpy中不能用连不等号，但是可以用np.logical_and()表示逻辑和；

np.setdiff1d(np.where(np.logical_and(a>=5,a<=10),a,1),([1]))：输出满足条件的元素的数组

np.vectorize(max,otyeps=[float]):将一个标量函数转换成一个矢量函数的方法。。。。虽然我也不清楚这个函数到底怎么用

a[:,[1,0,2]]改变原来二维数组的列，新列的index在最后一个数组中；arr[[1,0,2],:]改变原来二维数组的行，新行的index在最后一个数组中。当index的参数值是-1时，默认将行（或列）倒序a[:,::-1],a[::-1]

5*np.random.random(15).reshape(5,3)+np.repeat(5,15).reshape(5,3):产生在5到10之间的随机二维数组；也可以用一下代码实现

np.random.randint(low=5, high=10, size=(5,3)) + np.random.random((5,3))

np.genfromtxt():

    genfromtxt函数创建数组表格数据

    genfromtxt主要执行两个循环运算。第一个循环将文件的每一行转换成字符串序列。第二个循环将每个字符串序列转换为相      应的数据类型。

    genfromtxt能够考虑缺失的数据,但其他更快和更简单的函数像loadtxt不能考虑缺失值

    genfromtxt唯一的强制参数是数据的来源。它可以是一个对应于一个本地或远程文件的名字字符串,或一个有read方法的file- like对象(如一个实际的文件或StringIO。StringIO对象)。如果参数是一个远程文件的URL,后者在当前目录中自动下载。输入文件 可以是一个文本文件或存档，目前,该函数识别gzip和bz2(bzip2)。归档文件的类型是检查文件的扩展：如果文件名以“.gz”结尾”,gzip存档;如果它结尾是“bz2”,bzip2存档。其中delimiter是分隔符类型

5.python矩阵运算表达式：

1.数组的相加，相当的随意，不用一样的行和列:

  a = np.array([1,2,3,4,5])

  b = a.reshape(-1,1)

  a+b 返回的是一个 5*5 的矩阵

其结果是一个数组所有行加上另一个数组的所有行，一个数组的所有列，加上另一个数组的所有列。返回两者之间最大行与最大列的矩阵。

 2.数组的乘积可以直接相乘，是对应位相乘，数组的求幂使用**。数组可以求转置，也是array.T,但是不能求逆

a.dot(b)、np.dot(a,b)是矩阵乘法

元素求e的幂：np.exp(array);元素开根号：np.sqrt(array)

3.几个基本的函数：array.max(),array.min(),array.mean(),array.sum(）

array.floor()向下取整；array.ravel()平坦化；

其中参数axis=1为行，axis=0为列

4.数组复制：

浅复制：.view()

# The view method creates a new array object that looks at the same data.

import numpy as np
a = np.arange(12)
b = a.view() # b是新创建出来的数组，但是b和a共享数据

b is a # 判断b是a？
# 输出 False
print (b)
# 输出 [ 0  1  2  3  4  5  6  7  8  9 10 11]
b.shape = 2, 6 # 改变b的shape，a的shape不会受影响
print (a.shape)
print (b)
# 输出 (12,)
[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]]
b[0, 4] = 1234 # 改变b第1行第5列元素为1234，a对应位置元素受到影响
print (b)
# 输出 [[   0    1    2    3 1234    5]
         [   6    7    8    9   10   11]]
print (a)
# 输出 [   0    1    2    3 1234    5    6    7    8    9   10   11]

深复制 : .copy()

# The copy method makes a complete copy of the array and its data.

import numpy as np
a = np.arange(12)
a.shape = 3, 4
a[1, 0] = 1234

c = a.copy()
c is a
c[0, 0] = 9999 # 改变c元素的值，不会影响a的元素
print (c)
print (a)
# 输出 [[9999    1    2    3]
 [1234    5    6    7]
 [   8    9   10   11]]
[[   0    1    2    3]
 [1234    5    6    7]
 [   8    9   10   11]]

5.利用==判断数组或矩阵中是否存在某个值:

6.将判断结果赋给某个变量

7.一次判断多个条件

8.矩阵的运算：  

a = np.matrix(np.array([[1,2,3],[2,1,3]]));

加法行列必须相同；对应元素相乘用 multiple ，矩阵相乘可直接写，但行和列要相等

matrix.T 表示转置 matrix.I 表示逆矩阵

9、矩阵对象的属性：

>>> m[0]                #取一行
matrix([[1, 2, 3]])
>>> m[0,1]              #第一行，第2个数据
2
>>> m[0][1]             #注意不能像数组那样取值了
Traceback (most recent call last):
  File "", line 1, in 
  File "/usr/lib64/python2.7/site-packages/numpy/matrixlib/defmatrix.py", line 305, in __getitem__
    out = N.ndarray.__getitem__(self, index)
IndexError: index 1 is out of bounds for axis 0 with size 1

#排序
>>> m=mat([[2,5,1],[4,6,2]])    #创建2行3列矩阵
>>> m
matrix([[2, 5, 1],
        [4, 6, 2]])
>>> m.sort()                    #对每一行进行排序
>>> m
matrix([[1, 2, 5],
        [2, 4, 6]])

>>> m.shape                     #获得矩阵的行列数
(2, 3)
>>> m.shape[0]                  #获得矩阵的行数
2
>>> m.shape[1]                  #获得矩阵的列数
3

#索引取值
>>> m[1,:]                      #取得第一行的所有元素
matrix([[2, 4, 6]])
>>> m[1,0:1]                    #第一行第0个元素，注意左闭右开
matrix([[2]])
>>> m[1,0:3]
matrix([[2, 4, 6]])
>>> m[1,0:2]
matrix([[2, 4]])

#矩阵拓展：np.tile
x=np.matrix([1,2,3])
np.tile(x,(2,4))

matrix.T transpose：返回矩阵的转置矩阵

matrix.H hermitian (conjugate) transpose：返回复数矩阵的共轭元素矩阵

matrix.I inverse：返回矩阵的逆矩阵

matrix.A base array：返回矩阵基于的数组

矩阵对象的方法：

all([axis, out]) :沿给定的轴判断矩阵所有元素是否为真(非0即为真)

any([axis, out]) :沿给定轴的方向判断矩阵元素是否为真，只要一个元素为真则为真。

argmax([axis, out]) :沿给定轴的方向返回最大元素的索引（最大元素的位置）.

argmin([axis, out]): 沿给定轴的方向返回最小元素的索引（最小元素的位置）

argsort([axis, kind, order]) :返回排序后的索引矩阵

astype(dtype[, order, casting, subok, copy]):将该矩阵数据复制，且数据类型为指定的数据类型

byteswap(inplace) Swap the bytes of the array elements

choose(choices[, out, mode]) :根据给定的索引得到一个新的数据矩阵（索引从choices给定）

clip(a_min, a_max[, out]) :返回新的矩阵，比给定元素大的元素为a_max，小的为a_min

compress(condition[, axis, out]) :返回满足条件的矩阵

conj() :返回复数的共轭复数

conjugate() :返回所有复数的共轭复数元素

copy([order]) :复制一个矩阵并赋给另外一个对象，b=a.copy()

cumprod([axis, dtype, out]) :返回沿指定轴的元素累积矩阵

cumsum([axis, dtype, out]) :返回沿指定轴的元素累积和矩阵

diagonal([offset, axis1, axis2]) :返回矩阵中对角线的数据

dot(b[, out]) :两个矩阵的点乘

dump(file) :将矩阵存储为指定文件,可以通过pickle.loads()或者numpy.loads()如:a.dump(‘d:\\a.txt’)

dumps() :将矩阵的数据转存为字符串.

fill(value) :将矩阵中的所有元素填充为指定的value

flatten([order]) :将矩阵转化为一个一维的形式，但是还是matrix对象

getA() :返回自己，但是作为ndarray返回

getA1()：返回一个扁平（一维）的数组（ndarray）

getH() :返回自身的共轭复数转置矩阵

getI() :返回本身的逆矩阵

getT() :返回本身的转置矩阵

max([axis, out]) ：返回指定轴的最大值

mean([axis, dtype, out]) :沿给定轴方向，返回其均值

min([axis, out]) ：返回指定轴的最小值

nonzero() :返回非零元素的索引矩阵

prod([axis, dtype, out]) :返回指定轴方型上，矩阵元素的乘积.

ptp([axis, out]) :返回指定轴方向的最大值减去最小值.

put(indices, values[, mode]) :用给定的value替换矩阵本身给定索引（indices）位置的值

ravel([order]) :返回一个数组，该数组是一维数组或平数组

repeat(repeats[, axis]) :重复矩阵中的元素，可以沿指定轴方向重复矩阵元素，repeats为重复次数

reshape(shape[, order]) :改变矩阵的大小,如：reshape([2,3])

resize(new_shape[, refcheck]) :改变该数据的尺寸大小

round([decimals, out]) :返回指定精度后的矩阵，指定的位数采用四舍五入，若为1，则保留一位小数

searchsorted(v[, side, sorter]) :搜索V在矩阵中的索引位置

sort([axis, kind, order]) :对矩阵进行排序或者按轴的方向进行排序

squeeze([axis]) :移除长度为1的轴

std([axis, dtype, out, ddof]) :沿指定轴的方向，返回元素的标准差.

sum([axis, dtype, out]) ：沿指定轴的方向，返回其元素的总和

swapaxes(axis1, axis2):交换两个轴方向上的数据.

take(indices[, axis, out, mode]) :提取指定索引位置的数据,并以一维数组或者矩阵返回(主要取决axis)

tofile(fid[, sep, format]) :将矩阵中的数据以二进制写入到文件

tolist() :将矩阵转化为列表形式

tostring([order]):将矩阵转化为python的字符串.

trace([offset, axis1, axis2, dtype, out]):返回对角线元素之和

transpose(*axes) :返回矩阵的转置矩阵，不改变原有矩阵

var([axis, dtype, out, ddof]) ：沿指定轴方向，返回矩阵元素的方差

view([dtype, type]) :生成一个相同数据，但是类型为指定新类型的矩阵。