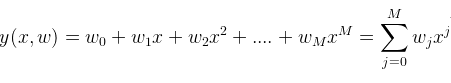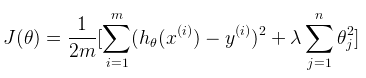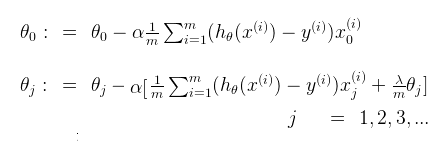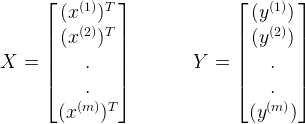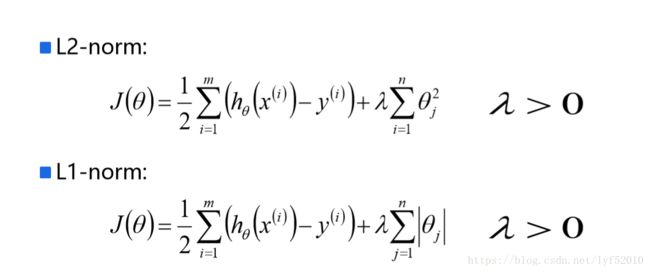机器学习(三)线性回归(Ridge,Lasso)的正则化
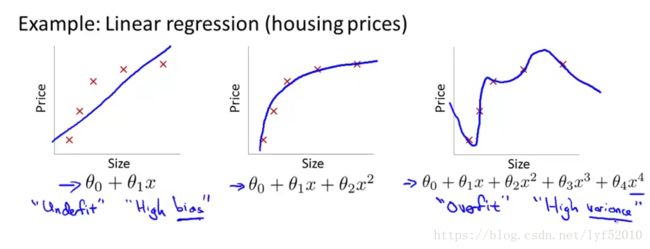
线性回归存在一个很重要的问题就是过拟合(overfitting)问题,所谓过拟合简单直白的说就是模型的训练误差极小,而检验误差很大。一个好的学习器不仅能够很好的拟合训练数据,而且能够对未知样本有很强的泛化能力,即低泛化误差。先来看看线性回归中的过拟合现象
图中左边的图表示的线性回归模型存在欠拟合现象(underfitting),欠拟合顾名思义就是对训练数据的拟合程度不够好,训练误差大。中间的线性回归模型是个拟合程度很好的模型。右边图表示的就是过拟合现象,能够看出它对训练数据拟合的非常好,但是预测能力很差,泛化能力很差。
因此,处理过拟合问题常用的方法有:
- 减少特征数量 主要方法有:人工的挑选重要的特征,去除不重要的特征。采用特征选择算法(在后面的博客中会介绍,在这不细说了) 但是这个方法在去除特征的同时,也去除了这部分特征所提供的信息。
- 正则化(regularization) 保留所有特征,但是减少参数
 的值。
的值。
线性回归正则化通过缩小参数的值,可以使多项式模型更加简单,直接举个例子吧(图片来源:ng machine learning课)
上图左边的二次曲线是我们希望的,右边的更高次的线性回归模型显然是过拟合的,但是如果在它的代价函数后面添加两项![]() 和
和![]() ,如果想让
,如果想让![]() 最小,那么
最小,那么![]() 和
和![]() 的值几乎要接近0,因此,右边的多项式几乎等价于左边的,又能够得到一个正确的线性回归模型。
的值几乎要接近0,因此,右边的多项式几乎等价于左边的,又能够得到一个正确的线性回归模型。
先来说说为什么增加正则项就能够有效避免过拟合(或者说是引入正则项的动机):假如对于一个多项式函数,
我们来看看随着多项式阶数的增加系数M是如何剧增的,见下表(来自PRML):
看完这个表应该一目了然,正则项为什么能够惩罚系数了。
因此,正则化线性回归(regularized linear regression)的代价函数(cost function)为:
其中![]() 为正则项,
为正则项,![]() 为正则系数。如果
为正则系数。如果![]() 设置的非常大,会使
设置的非常大,会使![]() ,将会产生欠拟合问题。因此应该选择合适的正则系数
,将会产生欠拟合问题。因此应该选择合适的正则系数![]() 。
。
我们的目标是![]() 即求得使
即求得使![]() 最小的参数
最小的参数![]() 。因此对正则化线性回归使用梯度下降(gradient descent),为:
。因此对正则化线性回归使用梯度下降(gradient descent),为:
之所以把![]() 单独写出来,是因为我们正则化的时候,不对
单独写出来,是因为我们正则化的时候,不对![]() 进行惩罚。如果上面的
进行惩罚。如果上面的![]() 的公式中的同类项合并下,则为:
的公式中的同类项合并下,则为:
因为![]() 始终为正,因此
始终为正,因此 ![]() 一般来说其值比1小一点点,因此
一般来说其值比1小一点点,因此![]() 相当于把
相当于把![]() 缩小了一点点。
缩小了一点点。
对于线性回归来说,除了通过梯度下降来求解参数![]() ,还可以通过正规方程(normal equation)用矩阵运算来直接求解参数
,还可以通过正规方程(normal equation)用矩阵运算来直接求解参数![]() 。对于样本X和label Y而言,可以如下表达:
。对于样本X和label Y而言,可以如下表达:
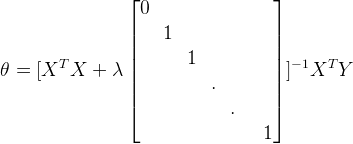
那么正则化线性回归的正规方程为:
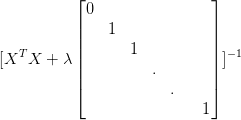
其中,上式中的对角矩阵维度是(n+1)*(n+1)。在以前的博客讲正规方程的时候讲过当![]() 时,
时,![]() 不存在,幸运的是正规化帮助我们解决了这个问题,即在正则化线性回归中,如果
不存在,幸运的是正规化帮助我们解决了这个问题,即在正则化线性回归中,如果![]() ,则
,则
是存在的,也即里面的矩阵是可逆的。
如果数据集的特征比样本点还多(XN×d,d>NXN×d,d>N)怎么办?是否还可以使用线性回归来做预测?答案是否定的,因为在计算 (XTX)−1(XTX)−1 的时候会出错。
为了解决这个问题,统计学家引入了岭回归(ridge regression)的概念。简单说来,岭回归就是在矩阵 XTXXTX上加一个 λIλI 使得矩阵非奇异,进而能对 XX+λIXX+λI 求逆。在这种情况下,回归系数的计算公式变为:
w=(XTX+λI)−1XTyw=(XTX+λI)−1XTy
岭回归最先用来处理特征数多于样本数的情况,
ridge regression
最为常见的就是对ww的模做约束,如ridge regression,岭回归,就是在线性回归的基础上加上l2l2-norm的约束,loss function是(习惯上一般会去掉前面线性回归目标函数中的常数项1n1n,同时为了后面推导的简洁性会加上一个1212):
JR(w)=12∥y−Xw∥2+λ2∥w∥2JR(w)=12‖y−Xw‖2+λ2‖w‖2
有解析解:
w^R=(XTX+λI)−1XTyw^R=(XTX+λI)−1XTy
其中λ>0λ>0是一个参数,有了正则项以后解就有了很好的性质,首先是对ww的模做约束,使得它的数值会比较小,很大程度上减轻了overfitting的问题;其次是上面求逆部分肯定可以解,在实际使用中ridge regression的作用很大,通过调节参数λλ,可以得到不同的回归模型。
实际上ridge regression可以用下面的优化目标形式表达:
minw12∥y−Xw∥2,s.t.∥w∥2<θminw12‖y−Xw‖2,s.t.‖w‖2<θ
也就是说,我依然优化线性回归的目标,但是条件是ww的模长不能超过限制θθ。上面两种优化形式是等价的,可以找到一 一对应的λλ和θθ。
稀疏约束,Lasso
先看一下几种范式(norm)的定义,
∥w∥2=(∑iwi2)1/2‖w‖2=(∑iwi2)1/2
∥w∥1=∑i|wi|‖w‖1=∑i|wi|
∥w∥0=∑i1(wi≠0)‖w‖0=∑i1(wi≠0)
如前面的ridge regression,对ww做2范式约束,就是把解约束在一个l2l2-ball里面,放缩是对球的半径放缩,因此ww的每一个维度都在以同一个系数放缩,通过放缩不会产生稀疏的解——即某些ww的维度是0。而实际应用中,数据的维度中是存在噪音和冗余的,稀疏的解可以找到有用的维度并且减少冗余,提高回归预测的准确性和鲁棒性(减少了overfitting)。在压缩感知、稀疏编码等非常多的机器学习模型中都需要用到稀疏约束。
稀疏约束最直观的形式应该是约束0范式,如上面的范式介绍,ww的0范式是求ww中非零元素的个数。如果约束∥w∥0≤k‖w‖0≤k,就是约束非零元素个数不大于k。不过很明显,0范式是不连续的且非凸的,如果在线性回归中加上0范式的约束,就变成了一个组合优化问题:挑出≤k≤k个系数然后做回归,找到目标函数的最小值对应的系数组合,是一个NP问题。
有趣的是,l1l1-norm(1范式)也可以达到稀疏的效果,是0范式的最优凸近似,借用一张图[1]: 
很重要的是1范式容易求解,并且是凸的,所以几乎看得到稀疏约束的地方都是用的1范式。
回到本文对于线性回归的讨论,就引出了Lasso(least absolute shrinkage and selection operator) 的问题:
minw12∥y−Xw∥2,s.t.∥w∥1<θ
参考:https://blog.csdn.net/u012328159/article/details/51089365
https://blog.csdn.net/xbinworld/article/details/44276389#t1
正规化方程Normal Equations解析
如果需要代做算法,可以联系我...博客右侧有联系方式。
一、正规化方程概念
假设我们有m个样本。特征向量的维度为n。因此,可知样本为{(x(1),y(1)), (x(2),y(2)),... ..., (x(m),y(m))},其中对于每一个样本中的x(i),都有x(i)={x1(i), xn(i),... ...,xn(i)}。令 H(θ)=θ0 + θ1x1 +θ2x2 +... + θnxn,则有
若希望H(θ)=Y,则有
X · θ = Y
我们先来回忆一下两个概念:单位矩阵 和 矩阵的逆,看看它们有什么性质。
(1)单位矩阵E
AE=EA=A
(2)矩阵的逆A-1
要求:A必须为方阵
性质:AA-1=A-1A=E
再来看看式子 X · θ = Y
若想求出θ,那么我们需要做一些转换:
step1:先把θ左边的矩阵变成一个方阵。通过乘以XT可以实现,则有
XTX · θ = XTY
step2:把θ左边的部分变成一个单位矩阵,这样就可以让它消失于无形了……
(XTX)-1(XTX) · θ = (XTX)-1XTY
step3:由于(XTX)-1(XTX) = E,因此式子变为
Eθ = (XTX)-1XTY
E可以去掉,因此得到
θ = (XTX)-1XTY
这就是我们所说的Normal Equation了。
二、Normal Equation VS Gradient Descent
Normal Equation 跟 Gradient Descent(梯度下降)一样,可以用来求权重向量θ。但它与Gradient Descent相比,既有优势也有劣势。
优势:Normal Equation可以不在意x特征的scale。比如,有特征向量X={x1, x2}, 其中x1的range为1~2000,而x2的range为1~4,可以看到它们的范围相差了500倍。如果使用Gradient Descent方法的话,会导致椭圆变得很窄很长,而出现梯度下降困难,甚至无法下降梯度(因为导数乘上步长后可能会冲出椭圆的外面)。但是,如果用Normal Equation方法的话,就不用担心这个问题了。因为它是纯粹的矩阵算法。
劣势:相比于Gradient Descent,Normal Equation需要大量的矩阵运算,特别是求矩阵的逆。在矩阵很大的情况下,会大大增加计算复杂性以及对计算机内存容量的要求。
什么情况下会出现Normal Equation,该如何应对?
(1)当特征向量的维度过多时(如,m <= n 时)
解决方法:① 使用regularization方式
or ②delete一些特征维度
(2)有redundant features(也称为linearly dependent feature)
例如, x1= size in feet2
x2 = size in m2
feet和m的换算为 1m≈3.28feet所以,x1 ≈ 3.282 * x2, 因此x1和x2是线性相关的(也可以说x1和x2之间有一个是冗余的)
解决方法:找出冗余的特征维度,删除之。
三、例子
y(i)表示价格,x(i)表示房屋面积和房间数:
样本数m=47。
step1:对数据进行预处理
给每一个x向量,都增加一个x0=1的分量。
m = 47;
x=[ones(m,1),ex3x];查看x矩阵:
step2:带入normal equation公式θ = (XTX)-1XTY,求解权重向量。
y=ex3y;
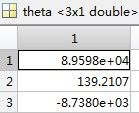
theta = inv(x'*x)*x'*y;求得θ向量为
如果我想预计“1650-square-foot house with 3 bedrooms”的价格,那么由X * θ = Y可知:
price = [1,1650,3]* theta ;我们取消matlab中的科学计数法,看看price的价格是多少:
>> format long g
>> price
price = 293081.464334897
我们在给出的样本中,找一个接近的样本比比看:
![]()
23号样本的房屋面积为1604,房间数也为3,它的价格为
![]()
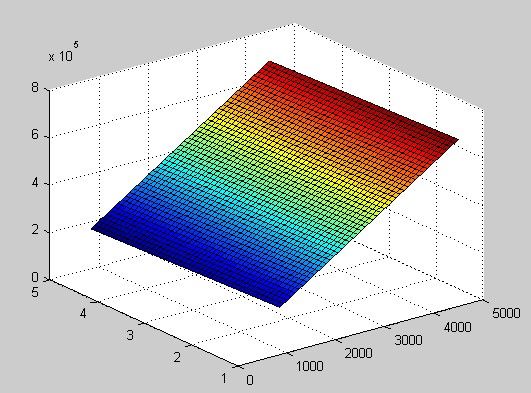
我们可以尝试画出H(θ)函数的图像看看:
先分别用min和max函数找出房屋面积(x1)和房间个数(x2)的最大和最小值,有
x1∈[852,4478]
x2∈[1,5]
x1=linspace(852,4478,47);
x2=linspace(1,5,47);
[xx1,xx2]=meshgrid(x1,x2);
h_theta = theta(1)*ones(47,47) + theta(2)*xx1 + theta(3)*xx2;
surf(xx1,xx2,h_theta);可以看到H(θ)为如下平面:
梯度下降需要预先确定学习速率、迭代次数,和数据规范化 Feature Scaling。