简单直白理解RBF神经网络及其MATLAB实例
RBF和GRNN和PNN神经网络有很多相似之处。后面继续讲GRNN和PNN神经网络。
学习RBF可以先和上一篇博文：BP神经网络做一个类比。
RBF神经网络
RBF神经网络和BP神经网络的区别就在于训练方法上面：RBF的隐含层与输入层之间的连接权值不是随机确定的，是有一种固定算式的。下面以精确型RBF为例。
假设每个样本有R维的特征。有S1个训练集样本。IW1表示训练集，即S1XR的一个矩阵。
此时，输入一个R维的测试集样本p，首先将p和IW1计算欧氏距离。
已知，我们要知道RBF径向基函数的效果是：
所谓径向基函数 (Radial Basis Function 简称 RBF), 就是某种沿径向对称的标量函数。 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 , 可记作 k(||x-xc||), 其作用往往是局部的 , 即当x远离xc时函数取值很小。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ^2) } 其中xc为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。
简单地说，就是某个测试集样本p和某个训练集样本越接近，即欧氏距离越小，那么在RBF作用后输出的值就越大。
假设这个样本p和训练集中某个样本（即IW1中某一列）很相似（即欧氏距离dist很小），那么输出结果a1中（a1维度是S1X1）就有一个值会很大。经过权重和偏置的作用后，再进入线性分类器中，就很容易可以分出来。这是我的直观的理解。
生成RBF的matlab函数：net = newrbe(P,T,spread)。只有一个参数spread需要调整。
P |
|
T |
|
spread |
Spread of radial basis functions (default = 1.0) |
The larger the spread is, the smoother the function approximation will be. Too large a spread can cause numerical problems.
也就是说，spread这个参数越大，RBF图像越平滑，RBF的输出差距不大，则所有输入的作用都会被减弱。
关于此算法，MATLAB文档中给出了很精炼的解释：
newrbe creates a two-layer network. The first layer has radbas neurons, and calculates its weighted inputs with dist and its net input with netprod. The second layer has purelin neurons, and calculates its weighted input withdotprod and its net inputs with netsum. Both layers have biases.
newrbe sets the first-layer weights to P', and the first-layer biases are all set to 0.8326/spread, resulting in radial basis functions that cross 0.5 at weighted inputs of +/– spread.（就是说这样设计出默认的RBF的效果是，关于X=0对称，横轴为+/-0.8333时函数的纵轴坐标值大约是0.5，表现在图中就是cross于这个点。如果加权后输入是+/- spread的话，正好产生此效果。）
The second-layer weights IW{2,1} and biases b{2} are found by simulating the first-layer outputs A{1} and then solving the following linear expression:
[W{2,1} b{2}] * [A{1}; ones] = T也就是说，RBF实际上是一个两层的神经网络。很简单，隐层是使用RBF作为激活函数的神经元，输出层采用线性函数的神经元，做一个线性分类。在前面的dist计算欧氏距离过程中，RBF采用高斯函数，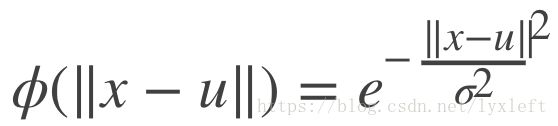
，实际上是将数据转化到高维空间，认为存在某个高维空间能够使得数据在这个空间是线性可分的。因此输出层是线性的。
上面也解释了本文开头中讲的，神经元之间非随机的权值是如何计算的：实际上，第一层的权值设为输入矩阵P的转置。而第二层的权值和偏置是要通过输入参数T、第一层的output结果来反推的。
时间太晚了，暂且简单粗暴记录于此。大家对RBF的含义有个认识即可！
下面是MATLAB文档中给的简单代码：
预测汽油辛烷值的例子：
（可见我上一篇讲BP神经网络的博文）
%% I. 清空环境变量
clear all
clc
%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra_data.mat
%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集――50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集――10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);
%% III. RBF神经网络创建及仿真测试
%%
% 1. 创建网络
net = newrbe(P_train,T_train,30);
%%
% 2. 仿真测试
T_sim = sim(net,P_test);
%% IV. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;
%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2));
%%
% 3. 结果对比
result = [T_test' T_sim' error']
%% V. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)
参考资料：
1、RBF神经网络简单介绍与MATLAB实现
2、MATLAB中RBF相关的文档
3、RBF的百度百科资料