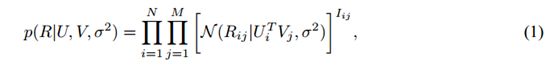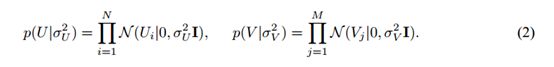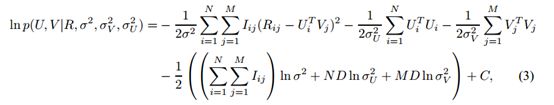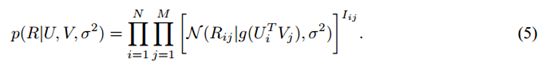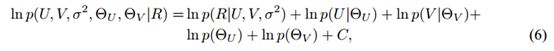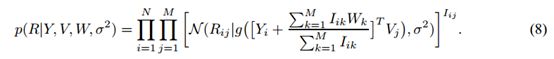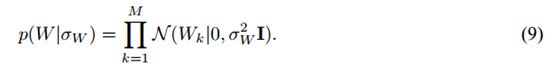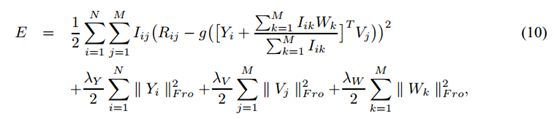概率矩阵分解（Probabilistic Matrix Factorization）

 摘要

很多现有的协同过滤的方法既不能处理非常大的数据集，也不能容易地应对有非常少的评价的用户。在这篇论文中，我们提出了概率矩阵分解（PMF）模型，它的规模与观察值的数目线性相关，并且更重要的是，它在非常大的、稀疏的和非常失衡的Netflix数据集上表现优异。我们更进一步地扩展PMF模型来包含一个适合的先验在模型参数中并且展示模型能力怎样可以被自动地控制。最后，我们引入一个有约束版本的PMF模型，它基于评价相似集合电影的用户可能有相似偏好的假设。这个结果模型对于有很少评价的用户能够归纳的相当好。当多个PMF模型的预测与受限玻尔兹曼机模型的预测线性结合时，我们达到了0.8861的误差率，这几乎比Netflix自己系统的分数提升了7%。

 

1 介绍

一种最流行的协同过滤的方法是基于低维度的因子模型。在这样的模型后面的思想是一个用户的态度或者偏好由少量的没有观察到的因子决定。在一个线性因子模型中，一个用户的偏好通过线性结合使用特定用户系数的物品因子向量建模。例如，对于N个用户和M个电影，N×M的偏好矩阵R由一个N×D的用户系数矩阵UT和一个D×M的因子矩阵V的乘积给出。训练这样的一个模型可以在给定的损失函数下，对于观测的N×M的目标矩阵R发现最好的矩阵秩为D的近似值。

多种多样的概率的基于因子的模型最近被提出。所有的这些模型能够被看作是隐藏因子变量有到代表用户评价的变量的定向连接的图解的模型。这些模型的主要缺点是很难得到精确的推断结果，这意味着对于计算在这些模型的隐藏因子上的后验分布需要潜在地慢的或者不准确的近似值。

基于最小化平方和距离的低秩逼近可能使用奇异值分解（SVD）找到。SVD发现给定秩的矩阵=V，它表示最小化到目标矩阵R的平方和距离。因为大部分现实的数据集是稀疏的，即在R中的大部分条目是缺失的。在那些情况下，平方和距离仅仅在目标矩阵R的被观察的条目中被计算。正如[9]中所展示的，这在一个困难的无法使用标准的SVD实现解决的非凸最优化问题中看上去是较次要的修正结果。

代替约束近似矩阵=V的秩，也就是因子的数目，[10]提出处罚U和V的范数。在这个模型的学习中，然而，要求解决一个稀疏的半定问题（SDP），使得这个方法对于包含数以百万计的观察值的数据集是不可实行的。

 

 

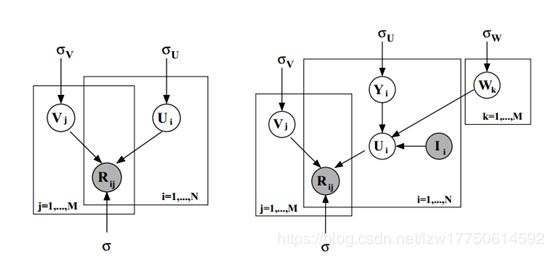
图1：左图展示了关于概率矩阵分解（PMF）的图模型；右图展示了关于有约束的PMF的图模型。

 

以上提到的很多协同过滤算法已经在Netflix Prize数据集（包含480189个用户，17770部电影和超过100百万的观测值[用户/电影/评价]三元组）上被应用来对用户评价建模。然而，因为两个原因，这些方法都没能证明是特别地成功。首先，以上提到的方法，除了基于矩阵分解的方法之外，对于大数据集的递增适应性都不够好。第二，大多数现有的算法对于有非常少评价的用户在做精确的预测上有困难。在协同过滤团体中的一个常例是去移除所有少于某些最小数字评价的用户。因此，反映在标准数据集（比如MovieLens和EachMovie）上的结果似乎是引人注目的，因为最困难的情况已经被移除了。例如，Netflix数据集是非常失衡的（不频繁评价的用户评价少于5部电影，然而频繁评价的用户评价超过10000部电影）。然而，因为标准测试集合包括完整范围的用户，Netflix数据集针对协同过滤算法提供了一个更加现实的和有用的标准检查程序。

这篇论文的目标是提出随观测值数目线性递增适应以及在非常稀疏和失衡的数据集（例如Netflix数据集）上表现优异的概率算法。在第2部分，我们提出利用两个更低秩的用户和电影矩阵的乘积对用户偏好矩阵建模的概率矩阵分解（PMF）模型。在第3部分，我们扩展PMF模型去包括在电影和用户特征向量上的自适应先验并且展示这些先验怎样可以被使用去自动地控制模型能力。在第4部分，我们引入一个基于评价相似集合的电影的用户有相似的偏好的假设的有约束版本的PMF模型。在第5部分，我们公布了实验结果，展示了PMF相比标准SVD模型有了相当大的提升。我们也展示了有约束的PMF和伴随可学习先验的PMF显著地提升了模型性能。我们的结果证明了有约束的PMF针对有很少评价的用户做更好的预测是特别有效的。

 

2 概率矩阵分解

假设我们有M部电影，N个用户，和从1到的整数评价值。表示用户i对电影j的评价，U∈和V∈是潜在的用户和电影特征矩阵，其中列向量和分别表示特定用户的和特定电影的潜在特征向量。因为模型性能通过计算在测试集合上的均方根误差（RMSE）来测量，我们首先采用一个含有高斯观测噪声的概率线性模型（见图1，左图）。我们定义在观测的评价上的条件分布：

是高斯分布（平均值为，方差为）的概率密度函数，是指标函数（如果用户i评价了电影j，该值为1；否则为0）。我们也放置了均值为0的球形高斯先验在用户和电影特征向量上：

在用户和电影特征上的后验分布的log函数由下列公式给出

C是一个不依赖参数的常量。最大化在含有固定不变的超参数的电影和用户特征上的log-后验等价于最小化含有二次正则项的平方误差和的目标函数：

其中和表示Frobenius范数。由等式4给出的目标函数的一个局部最小值可以通过在U和V上执行梯度下降来找到。注意这个模型可以被看作是SVD模型的一个概率的扩展，因为如果所有的评价都已经观测到，以先验方差趋向于无穷为限，由等式4给出的目标会还原到SVD目标。

                             

 1真实值的评价能够通过在这篇论文中描述的模型容易地被处理。（此为脚注）

 

在我们的实验中，代替使用一个简单的线性-高斯模型（能够在有效的评价值之外做预测），在特定用户和特定电影特征向量之间的点积通过逻辑函数g(x)=1/(1+exp(-x))传递（它限制预测的范围）：

我们使用函数t(x)=(x-1)/(K-1)映射评价1,…,K到区间[0,1]，所以有效评价值的范围匹配我们的模型做的预测的范围。使用最陡的下降最小化上面给出的目标函数会花费与观测值数目线性相关的时间。当模型被训练到有30个因子时，这个算法在Matlab中的一个简单实现允许我们在少于一个小时的时间内通过完整的Netflix数据集做一遍清扫。

 

3 关于PMF模型的自动能力控制

能力控制对于使PMF模型良好地推广是必要的。假设有足够多的因子，PMF模型能够比较好的近似随机给出的矩阵。控制PMF模型能力的最简单的方式是改变特征向量的维数。然而，当数据集是失衡的，也就是在不同行或列上的观测值的数目显著地不同，这个方法会失败，因为任意单个数目的特征维度对于某些特征向量太高，而对于其他的太低。在上面被定义的正则化参数（例如和）提供一个更灵活的正则化的方法。也许对于这些参数发现适当的值的最简单的方式是考虑合理参数值的一个集合，以在该集合中的参数的每个设置训练模型，并且选择在验证集合上执行的最好的模型。这个方法的主要缺点是它的计算代价昂贵，因为代替训练单个模型，我们不得不训练大量模型。我们将展示由[6]提出的方法，它起初被应用到神经网络上，可以被用来针对PMF模型的正则化参数自动地决定适当的值，并且没有显著地影响需要去训练模型的时间。

正如以上展示，在意义上通过两个以处罚Frobenius范数的方式正则化的低秩的矩阵的乘积近似一个矩阵的问题可以被看作是在低秩矩阵的行上含有球形高斯先验的概率模型中的MAP估计。该模型的复杂度通过超参数控制：噪声方差σ2和先验参数（上面的σu2和σV2）。针对超参数引入先验和最大化在正如在[6]中建议的参数和超参数的模型的log-后验允许模型复杂度基于训练数据自动地被控制。在这个结构中对于用户和电影特征向量使用球形先验会导致含有自动地被挑选的λu和λv的PMF的标准形式。这个正则化的方法允许我们使用比简单的特征矩阵的Frobenius范数的处罚更加成熟的方法。例如，我们对于特征向量可以使用伴随除了可调整的方法之外还有对角线的或者甚至完整的协方差矩阵的先验。高斯先验的混合物也能够被十分容易地处理。

总的来说，我们发现了一个通过最大化以下给出的log-后验的参数和超参数的点估计

其中ΘU和Θv分别是关于在用户和电影特征向量之上的先验的超参数，C是一个不依赖参数或者超参数的常量。

当先验是高斯的，如果电影和用户特征向量是保持固定的，最优的超参数能够以不公开的形式被找到。因此为了简化学习，我们交替进行最优化超参数和使用固定超参数值的最陡的上升更新特征向量。当先验是一个高斯混合物时，超参数能够通过执行EM的一个简单步骤被更新。在我们所有的实验中，我们对于超参数使用了不合适的先验，但是扩展不公开的更新去处理关于超参数的成对的先验的形式是容易的。

 

4 有约束的PMF

一旦一个PMF模型已经适应，有很少评价的用户将会有与先验平均值或者平均用户接近的特征向量，所以针对那些用户的预测的评价将接近电影平均评价。在这个部分，我们引入了一种约束特定用户的特征向量的额外的方式，它对不频繁的用户有着大大的影响。

W∈RDxM是一个潜在的相似度约束矩阵。我们对于用户i定义特征向量正如：

其中I是观测的指标矩阵（如果用户i评价了电影j，Iij的值为1；否则为02）。直观地，W矩阵的ith列捕捉某个用户已经评价某部特定的电影对该用户的特征向量的先验平均值产生的影响。因此，已经看过相同（或相似）的电影的用户对于他们的特征向量将会有相似的先验分布。注意Yi可以被看作是为了得到关于用户i的特征向量Ui而添加到先验分布的平均值的分支。在无约束的PMF模型中，Ui和Vi是相等的，因为先验平均值固定为0（见图1）。我们现在定义在观测到的评价上的条件分布正如

我们通过放置一个均值为零的球形高斯先验在以下公式上来正则化潜在的相似度约束矩阵W：

 

                                      

2如果没有关于某个用户i的评价信息是可获得的，也就是，Ii向量的所有条目都是0，在等式7中的系数的值被设置为0。

 

正如伴随着PMF模型，最大化log-后验等价于最小化含有二次正则项的平方误差和函数：

和然后我们可以在Y，V，W上执行梯度下降去最小化由等式10给出的目标函数。对于有约束的PMF模型的训练时间线性地与观测值数目递增适应，它允许有一个快的、简单的实施。正如我们在我们的实验结果部分所展示，该模型表现得比一个简单的无约束的PMF模型好很多，尤其是在不频繁的用户上。

 

5.实验结果

5.1 Netflix数据的描述

根据Netflix，在1998年10月与2005年12月之间的数据被收集并且表示出了在这段时期Netflix获得的所有评价的分布。该训练数据集由来自于480189个随机选择的无个性特征的用户对17770个电影标题做的100480507个评价组成。作为训练数据的部分，Netflix也提供验证数据，包含1408395个评价。除了训练和验证数据，Netflix也提供一个包含伴随有抑制的评价的2817131个用户/电影对的测试集合。这些对挑选自在训练数据集中关于用户的一个子集的最近的评价。为了减少烦扰很多在机器学习文学中的经验主义的比较的测试集合上的无意识的过拟合，性能通过提交预测的评价到Netflix（然后Netflix公告在该测试集合的未知的一半上的均方根误差）上来评估。作为一个基准线，Netflix提供它自己的在同样数据上训练的系统的测试分数，该分数为0.9514。

为了提供关于不同算法的性能的额外的理解，我们从Netflix数据中通过任意地选择50000个用户和1850部电影创造了一个更小的和更加难解的数据集。该小数据集包含1082982个用于训练的和2462个用于验证的用户/电影对。在该训练数据集中的超过50%的用户有少于10的评价。

 

5.2 训练的细节

为了加速训练，代替执行批学习，我们细分Netflix数据为规模为100000（用户/电影/评价 三元组）的小批数据，并且在每个小批之后更新特征向量。在尝试关于学习率和动量的不同的值以及用D的不同值做实验之后，我们选择使用0.005的学习率，0.9的动量，正如该参数的设置对我们已经尝试的D的所有值表现优异。

 

5.3 伴随适应先验的PMF的结果

为了评价伴随适应先验的PMF模型的性能，我们使用了含有10维特征的模型。这个维度被选择是为了证明甚至当特征的维度是相对地低时，类似SVD的模型仍然能过拟合并且通过自动地正则化那样的模型，得到了一些性能上的增益。我们比较一个SVD模型，两个先验固定的PMF模型，和两个伴随适应先验的PMF模型。该SVD模型被训练去仅针对目标矩阵的观测的条目最小化平方和距离。该SVD模型的特征向量以任何方式不被正则化。这两个先验固定的PMF模型在它们的正则化参数上不同：一个（PMF1）有λU=0.01和λv=0.001，然而另一个（PMF2）有λu=0.001和λv=0.0001。这第一个伴随适应先验的PMF模型（PMFA1）在用户和电影特征向量上有伴随球形协方差矩阵的高斯先验，然而第二个模型（PMFA2）有对角线的协方差矩阵。在这两个例子中，适应先验含有可调整的方法。先验参数和噪声协方差分别在每10个和100个特征矩阵更新后被更新。这些模型基于在验证集合上的均方根误差来比较。

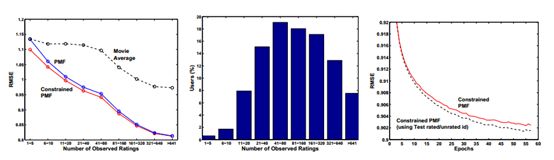
图2：左图：SVD，PMF和伴随适应先验的PMF的性能，使用10维特征向量，在完整的Netflix验证数据上。右图：SVD，概率矩阵分解（PMF）和约束的PMF的性能，使用30维特征向量，在验证数据上。y轴展示RMSE（均方根误差），x轴展示训练次数或者传递次数的数目，凭借完整的训练数据集。

 

比较的结果展示在图2（左图）中。注意关于伴随球形协方差的PMF模型的曲线没有被展示因为它实际上和关于伴随对角线的协方差的模型的曲线是同样的。基于最低的均方根误差来比较模型达到且超过了训练的时间，我们看到SVD模型在接近训练结束严重地过拟合之前几乎和适度正则化的PMF模型（PMF2）（0.9258 与 0.9253）一样。然而PMF1没有过拟合，它显然欠拟合，因为它达到仅0.9430的均方根误差。这些伴随适应先验的模型明显的优于竞争的模型，达到0.9197（对角线的协方差）和0.9204（球形协方差）的均方根误差。这些结果暗示凭借适应先验的自动正则化在实践中表现优异。而且，我们的关于伴随更高维度的特征向量的初步结果暗示在性能上的缺口是由于适应先验的使用可能随着特征向量提升的维度成长。然而对角协方差矩阵的使用不会导致在球形协方差矩阵上的显著地提升，对角协方差可能对于自动正则化PMF训练算法的贪婪版本是适当的，其中特征向量一次被学习一个维度。

 

5.4 约束的PMF的结果

对于包含约束的PMF模型的实验，我们使用30维特征（D=30），因为这个选择导致在验证集合上的最好的模型性能。在[20,60]范围的D的值产生相似的结果。SVD，PMF和约束的PMF的在小数据集上的性能结果被展示在图3中。在所有的三个模型中的这些特征向量被初始化为相同的值。对PMF和约束的PMF模型，正则化参数被设置为λu=λY=λV=λW=0.002。明显地，简单的SVD模型重重地过拟合。约束的PMF模型比无约束的PMF模型的表现要好很多并且聚集要快很多。图3（右图）展示了约束特定用户的特征对不频繁用户的预测的影响。对于在训练数据集中的一组有少于5个评价的用户的PMF模型的性能实际上和总是预测每部电影的平均评价的电影平均算法的性能是同样的。约束的PMF模型，然而，对于伴随少量评价的用户表现要好很多。随着评价的数目增加，PMF和约束的PMF展示了相似的性能。

 

图3：左图：在验证数据上的SVD，概率矩阵分解（PMF）和约束的PMF的性能。y轴展示RMSE（均方根误差），x轴展示训练次数或者传递次数，凭借完整的训练数据集。右图：约束的PMF，PMF和总是预测每部电影的平均评价的电影平均算法的性能。在训练数据中用户按观测的评价的数目分组。

 

 

图4：左图：约束的PMF，PMF和总是每部电影的平均评价的电影平均算法的性能。在训练数据中，用户按观测的评价的数目分组，伴随有x轴展示那些组，y轴展示在完整的Netflix验证数据上对于每个这样的组的RMSE。中间的图：在训练数据集中的用户的分布。右图：约束的PMF和利用额外的从测试数据集中获得的评价/未评价的信息的约束的PMF的性能。

 

 约束的PMF模型的另一个有趣的方面是即使我们仅仅知道用户评价了什么电影，但是不知道评价的值，该模型能够比电影平均模型做更好的预测。对于小数据集，我们任意地抽样额外的50000个用户，并且对于每个用户收集了用户已经评价的电影的一个列表，然后丢弃了真实的评价。约束的PMF模型在验证集合上达到了1.0510的均方根误差与对于简单的电影平均模型的1.0726的均方根误差相比较。该实验强有力的暗示了仅仅知道用户评价了哪些电影，但是不知道真实的评价，仍然能够帮助我们对用户的偏好更好的建模。

 在完整Netflix数据集上的性能结果与在小数据集上的结果相似。对于PMF和约束的PMF模型，正则化参数被设置为λU=λY=λV=λW=0.001。图2（右图）展示了约束的PMF显著地优于无约束的PMF模型，达到了0.9016的均方根误差。一个简单的SVD达到大约0.9280的均方根误差并且在大约10次训练后开始过拟合。图4（左图）展示了约束的PMF模型对于有非常少评价的用户能够归纳的更好。注意在训练数据集中超过10%的用户有少于20个评价。随着评价的数目增加，来自于等式7中的分支的影响变小，PMF和约束的PMF达到相似的性能。

 在Netflix数据集中有信息的更加精细的资源。Netflix提前告知我们哪些用户/电影对出现在测试集合中，所以我们有一个额外的类别：电影被看过，但是其评价是未知的。这是关于在测试集合中出现若干次的用户的信息的一个有价值的资源，尤其是如果他们在训练集合中有仅仅少数的评价。约束的PMF模型能够容易地将这个信息纳入考虑范围。图4（右图）展示了这个信息的额外资源更进一步地提升模型性能。

 当我们线性地结合PMF，伴随可学习的先验的PMF，约束的PMF的预测，我们在测试集合上达到了0.8970的误差率。当多个PMF模型的预测与多个RBM模型的预测线性地结合时，最近在[8]中被引入，我们达到了0.8861的误差率，这几乎比Netflix自己系统的分数提升了7%。

 

6 总结和讨论

在这篇论文中，我们提出概率矩阵分解（PMF）和它的两个派生物：伴随可学习的先验的PMF和约束的PMF。我们也证明了这些模型可以被有效地训练和成功应用到包含超过100百万的电影评价的大规模数据集。

在训练PMF模型中的效率来自于发现模型参数和超参数的唯一的点估计，而不是推理在它们上的完整的后验分布。如果我们采用了完整的贝叶斯定理的方法，我们将放置超先验在超参数上并且凭借MCMC方法执行推断的结果。尽管该方法计算代价更加昂贵，但是初步结果强有力地暗示了已提出的PMF模型的完整的贝叶斯定理的处理将导致在预言准确性中的显著地提升。

 

致谢

我们感谢Vinod Nair和Geoffrey Hinton给了很多有帮助的讨论。该研究被NSERC支持。

 

参考文献

[1] Delbert Dueck and Brendan Frey. Probabilistic sparse matrix factorization. Technical Report PSI TR 2004-023, Dept. of Computer Science, University of Toronto, 2004.
[2] Thomas Hofmann. Probabilistic latent semantic analysis. In Proceedings of the 15th Conference on Uncertainty in AI, pages 289–296, San Fransisco, California, 1999. Morgan Kaufmann.
[3] Benjamin Marlin. Modeling user rating profiles for collaborative filtering. In Sebastian Thrun, Lawrence K. Saul, and Bernhard Sch¨olkopf, editors, NIPS. MIT Press, 2003.
[4] Benjamin Marlin and Richard S. Zemel. The multiple multiplicative factor model for collaborative filtering. In Machine Learning, Proceedings of the Twenty-first International Conference (ICML 2004), Banff, Alberta, Canada, July 4-8, 2004. ACM, 2004.
[5] Radford M. Neal. Probabilistic inference using Markov chain Monte Carlo methods. Technical Report CRG-TR-93-1, Department of Computer Science, University of Toronto, September 1993.
[6] S. J. Nowlan and G. E. Hinton. Simplifying neural networks by soft weight-sharing. Neural Computation, 4:473–493, 1992.
[7] Jason D. M. Rennie and Nathan Srebro. Fast maximum margin matrix factorization for collaborative prediction. In Luc De Raedt and Stefan Wrobel, editors, Machine Learning, Proceedings of the TwentySecond International Conference (ICML 2005), Bonn, Germany, August 7-11, 2005, pages 713–719. ACM, 2005.
[8] Ruslan Salakhutdinov, Andriy Mnih, and Geoffrey Hinton. Restricted Boltzmann machines for collaborative filtering. In Machine Learning, Proceedings of the Twenty-fourth International Conference (ICML 2004). ACM, 2007.
[9] Nathan Srebro and Tommi Jaakkola. Weighted low-rank approximations. In Tom Fawcett and Nina Mishra, editors, Machine Learning, Proceedings of the Twentieth International Conference (ICML 2003), August 21-24, 2003, Washington, DC, USA, pages 720–727. AAAI Press, 2003.
[10] Nathan Srebro, Jason D. M. Rennie, and Tommi Jaakkola. Maximum-margin matrix factorization. In Advances in Neural Information Processing Systems, 2004.
[11] Michael E. Tipping and Christopher M. Bishop. Probabilistic principal component analysis. Technical Report NCRG/97/010, Neural Computing Research Group, Aston University, September 1997.
[12] Max Welling, Michal Rosen-Zvi, and Geoffrey Hinton. Exponential family harmoniums with an application to information retrieval. In NIPS 17, pages 1481–1488, Cambridge, MA, 2005. MIT Press.

 

原文下载链接：http://papers.nips.cc/paper/3208-probabilistic-matrix-factorization