布隆过滤器:实现大数据去重
位图
位图法(bitmap),采用每一位来存储一种状态,通常用于存储状态比较少,数据量很大的情况。位图、布隆过滤器应用很广泛,很多编程语言都有其实现,例如 Java 中的 BitSet,Redis 中也有提供 BitMap 位图类。
举个例子来说明一下位图的核心思想,假设当前有十个整数(1,5,7,4,8,9,2,0,3,6),我们要判断另一个整数是否存在在这十个整数中,效率最高的做法是将这十个数据存储到数组中,表示一个数据是否存在可以用 0 或 1 来表示,如图:

当我们要查找数据 11是否存在时,只需要判断A[11]是否为1就可以了。
那么当我们面对的是海量数据时,该如何处理才能最省内存呢?
例如,现在有一千万整数,整数的范围在 1~100,000,000 之间,若依旧采用上述方法,则需要一千万个单位的数组空间,整型数组一个单位占 4 字节,约需要 40MB 的空间。
对于每个数据而言,我们只需要存储的是这个数据是否存在,其实完全可以用一位来表示一个数据是否存在,那么根据数据大小范围,一共需要 1 亿位,大约 12 MB多。可以发现占用空间节约了很多。
位图实现代码:
public class BitMap { // Java 中 char 类型占 16bit,也即是 2 个字节
private char[] bytes;
private int nbits; //存储的数据量
public BitMap(int nbits) {
this.nbits = nbits;
this.bytes = new char[nbits/16+1];
}
public void set(int k) {
if (k > nbits)
return;
int byteIndex = k / 16;
int bitIndex = k % 16;
bytes[byteIndex] |= (1 << bitIndex);
}
public boolean get(int k) {
if (k > nbits)
return false;
int byteIndex = k / 16;
int bitIndex = k % 16;
return (bytes[byteIndex] & (1 << bitIndex)) != 0;
}
}
综上可以发现,位图在数据量很大的时候可以实现高效查找和插入,并且空间消耗不大。
布隆过滤器
布隆过滤器是在位图的基础上再次进行优化改造而成的。
思考一下开篇的例子中,一千万个数据,如果每个数据的范围是 1~1,000,000,000 那么,使用位图存储的话,占用的空间是多少?
答案是 10亿 位,即120MB,可以发现假如数据的范围很大的话,占用空间不减反增。
其实我们可以仍旧使用 1亿 位的空间来存储,只不过需要使用哈希函数来把所有数据都落在这 1亿 位中。
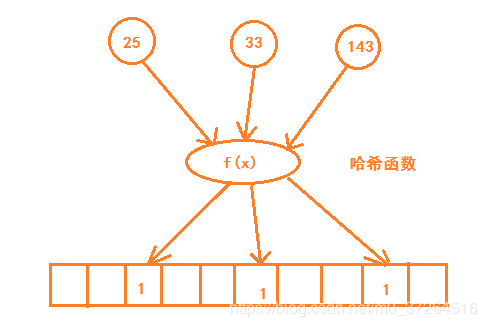
若按照上图中的方案存储,假设哈希函数是对位数取余,那么 1 和 100000001 得到的余数是一样的,即存在哈希冲突。
为了减少哈希冲突,我们可以采用多个哈希函数,例如采用 K 个哈希函数,那么数据 n 对应的哈希值有 K 个,分别记录这 K 个位置的值。

这就是布隆过滤器的核心思想,可以发现布隆过滤器比位图更省空间。但依旧是以位图为基础。
布隆过滤器容易导致误判,并且只会对已经存在的情况出现误判,若查询不存在则肯定不存在,如图:
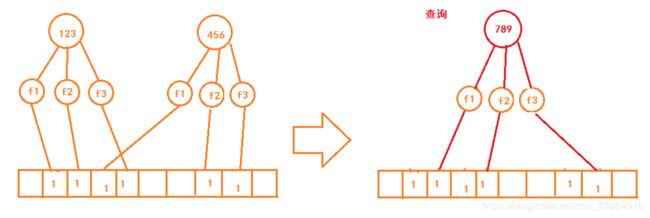
因此布隆过滤器适用于支持一定量容错的场景下。例如搜索引擎爬虫在爬取页面的时候,记录所有的URL是否已经爬取,存在一定的误判影响不大。又比如统计网站的访问量时,同一个用户进行去重,也不需要非常准确。
布隆过滤器效率
以爬虫爬取URL为例,要查询一个URL是否已经爬取,采用散列表存储时,在判断散列冲突的拉链下的URL时,需要从内存中读取URL并进行字符串匹配,而布隆过滤器则只需要将URL进行一系列哈希函数的计算,得到结果。
因此,散列表是内存密集型的,而布隆过滤器是 CPU 密集型的。显然,布隆过滤器效率比散列表高。
拓展
当布隆过滤器中位图的 true 个数越来越多时,误判会越来越严重,因此,当不知道数据规模时,应该使用会自动扩容的布隆过滤器。
当位图中 true 个数比例超过一定阈值时,新建一个位图,新增的数据就直接放在新位图中,查询时则需要从所有位图中都查询一遍。