MySQL数据库索引原理:B+树原理分析
数据库索引
在实际开发中,通常数据都是存储在数据库中,主流的比如 MySQL,Orcale等。数据库中的索引是提高数据库查询效率的有效手段之一,那么索引是如何实现的呢?
为了简化问题,我们将索引的问题抽象出来,常见的数据库操作中,有如下两条 SQL 语句:
select * from student where student_id = 20182937
select * from student where math_grade > 60 and math_grade < 90
这两条 SQL 语句要实现更加快速查找,索引的底层数据结构该如何设计呢?
方案有很多种,比如使用红黑树作为底层数据结构,那么查找某一个值的效率是O(1),但是红黑树并不支持快速区间查找,对于区间查找,很容易想到可以用跳表,但是跳表占用的空间比较多。
实际数据库中采用的数据结构跟跳表很相似,叫做 B+ 树
改造二叉查找树
B+ 树是由二叉查找树改造而成,将数据用双向链表串联,在此基础上构建二叉查找树(类比跳表中的多层索引),如图:
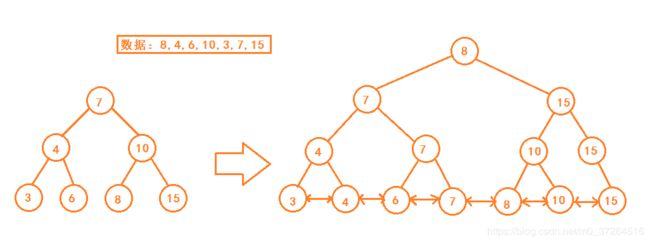
观察图很容易发现,在查找区间段的值时,只需要在树中查找到区间起始值最近的节点,再顺着链表往后遍历即可。
问题一:数据量大,内存不够
现在我们已经实现了既支持单节点快速查找,又支持区间查找的数据结构了,假设现在我们将其应用于实际中,如果现在有几千万几亿的数据量需要建立索引,将改造后的二叉查找树放在内存中会相当耗内存(多个表建立索引,内存完全不够)。
问题二:空间足够,效率过低
这个时候时间换空间的思想就可以派上用处了,可以将索引存储于硬盘,硬盘的存取速度与内存差好几个量级,磁盘中一次读取或访问就是一次 IO 操作,当数据量很大时,树的深度很深,则需要很多次 IO 操作,时间效率不够。
那么如何优化存储于磁盘中的时间效率呢?
通过降低 IO 操作次数可以有效增加时间效率,而 IO 操作次数与树的深度有关,如此可以想到,将二叉查找树转换成 m叉查找树,若m比 2 大,则必然树的深度会减小。
B+ 树
最后我们得到了m叉查找树与双向链表结合的一种数据结构,也就是B+ 树。
以int型索引为例,以下为 B+ 树的节点数据结构定义:
/**
* 这是 B+ 树非叶子节点的定义。
*
*/
public class BPlusTreeNode {
public static int m = 5; // 5 叉树
public int[] keywords = new int[m-1]; // 键值,用来划分数据区间
public BPlusTreeNode[] children = new BPlusTreeNode[m];// 保存子节点指针
}
/**
* 这是 B+ 树中叶子节点的定义。
*
* B+ 树中的叶子节点跟内部结点是不一样的,
* 叶子节点存储的是值,而非区间。
* 这个定义里,每个叶子节点存储 3 个数据行的键值及地址信息。
*/
public class BPlusTreeLeafNode {
public static int k = 3;
public int[] keywords = new int[k]; // 数据的键值
public long[] dataAddress = new long[k]; // 数据地址
public BPlusTreeLeafNode prev; // 这个结点在链表中的前驱结点
public BPlusTreeLeafNode next; // 这个结点在链表中的后继结点
}
通过上述代码,有两个问题:
- m 叉树中的 m 是不是越大越好
- 如何处理写入过多后,节点的子节点数超过 m 如何处理
问题一
操作系统中,不管是从内存还是硬盘中读取数据,数据的单位都是以页为单位的,要知道系统中每一页大小,可以 getconfig PAGE_SIZE 命令查看,通常是 4KB,因此如果 m 值越大时,树的深度越小,但是当每个节点存储的数据大于一页的大小时,IO 操作并不会减少,甚至可能增加。
因此,m的大小取值应该尽量以每个节点大小接近页的大小。
以上面代码为例,m 计算公式:
PAGE_SIZE = (m-1)*4[keywordss 大小]+m*8[children 大小]
叶子节点中 k 的值:
PAGE_SIZE = k*4[keyw.. 大小]+k*8[dataAd.. 大小]+8[prev 大小]+8[next 大小]
问题二
当一个节点的子节点数超过 m 个时,我们可以将其分裂成两个节点。节点分裂后,上层父节点可能超过 m 个,因此递归的向上分裂即可。
在具有索引时,插入和删除操作的速度均会降低,因为插入和删除操作都会导致数据量的变化,就需要更新索引。
在频繁的删除操作后,可能导致部分节点的子节点数很少,则查询效率会下降,那么该如何处理呢?
方法很简单,可以设一个阈值(m/2),节点的子节点数低于这个节点时,将它与兄弟节点合并,合并后子节点数可能会超过 m,此时再分裂即可。
B+ 树特点总结
B+ 树通过多叉树的形式存储于磁盘中,实现了时间、空间的平衡。
B+ 树的特点如下:
- 每个节点的子节点数大于 m/2,小于等于m
- 根节点子节点数可以小于 m/2
- m 叉树存的是索引,不是数据,类似跳表的索引
- 叶子节点存储数据,并使用双向链表串联,方便按区间查找
- 通常根节点在内存中,其余节点在硬盘中
拓展:B树,B-树
B- 树实际就是 B 树,而不是区别于 B+ 树的 B- 树(B 减树),本质上这不是减号,而是横杆,即 B-Tree 的缩写。
B 树和 B+ 树的区别:
- B+ 树中,树的节点存储的是索引,叶子节点是数据,而B树中树的节点都是数据。
- B 树叶子节点不需要双向链表串联。
通俗的说就是,B 树只是一个节点子节点数在(m/2,m)之间的多叉查找树。