【数据结构笔记】二叉搜索树及其相关算法
简介
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
如下图所示:
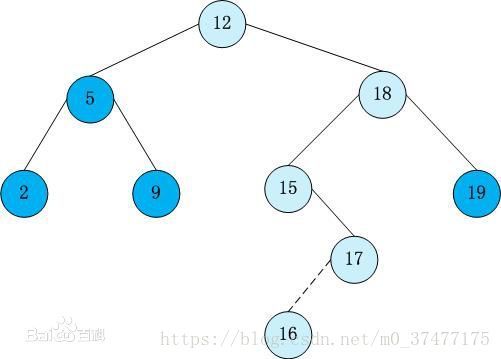 图片来自百度百科
图片来自百度百科
二叉排序树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉排序树的存储结构。
| 中序遍历二叉排序树可得到一个关键字的有序序列 |
一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。搜索,插入,删除的复杂度等于树高,O(log(n)).
查找算法
在二叉排序树b中查找x的过程为:
若b是空树,则搜索失败,否则:
若x等于b的根结点的数据域之值,则查找成功;否则:
若x小于b的根结点的数据域之值,则搜索左子树;否则:
查找右子树。
插入算法
向一个二叉排序树b中插入一个结点s的算法,过程为:
若b是空树,则将s所指结点作为根结点插入,否则:
若s->data等于b的根结点的数据域之值,则返回,否则:
若s->data小于b的根结点的数据域之值,则把s所指结点插入到左子树中,否则:
把s所指结点插入到右子树中。
Leetcode 230. 二叉搜索树中第K小的元素
给定一个二叉搜索树,编写一个函数kthSmallest来查找其中第k个最小的元素。
注意:
你可以假设k总是有效的,1≤ k ≤二叉搜索树元素个数。
进阶:
如果经常修改二叉搜索树(插入/删除操作)并且你需要频繁地找到第k小值呢? 你将如何优化kthSmallest函数?
法1:递归
按顺序中序遍历每个节点,并实时的减小K的值,直到K的值为0,则当前节点的值即为第K小的元素。
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def kthSmallest(self, root, k):
"""
:type root: TreeNode
:type k: int
:rtype: int
"""
if root:
x = self.kthSmallest(root.left,k)
if k == 0:
return x
else:
k = k -1
if k == 0:
return root.val
else:
return self.kthSmallest(root.right,k)法2:迭代查找
| 使用栈,先进先出 |
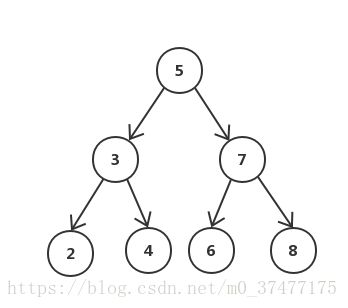
例子,二分查找树:
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
# 返回对应节点TreeNode
def KthNode(self, pRoot, k):
# write code here
if k == 0 or pRoot is None:
return None
q = [(pRoot, False)]
while q:
cur, flag = q.pop()
if cur:
if flag:
k -= 1
if k==0:
return cur
else:
q.append((cur.right, False))
q.append((cur, True))
q.append((cur.left, False))中序遍历操作过程,q中的元素变化:
- 5F
- 7F 5T 3F
- 7F 5T 4F 3T 2F
- 7F 5T 4F 3T N 2T N
- 7F 5T 4F 3T N 2T
- 7F 5T 4F 3T N ———————> 2
- 7F 5T 4F 3T
- 7F 5T 4F ———————> 2,3
- 7F 5T N 4T N
- 7F 5T N 4T
- 7F 5T N ————————>2,3,4
- 7F 5T
- 7F ————————>2,3,4,5
- 8F 7T 6F
- 8F 7T N 6T N
- 8F 7T N 6T
- 8F 7T N ———–>2,3,4,5,6
- 8F 7T
- 8F —————>2,3,4,5,6,7
- N 8T N
- N 8T
- N —————->2,3,4,5,6,7,8
二叉树遍历非递归模板
中序遍历(左右根)
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):
def inorderTraversal(self, root):
"""
:type root: TreeNode
:rtype: List[int]
"""
result, stack = [], [(root, False)]
while stack:
cur, flag = stack.pop()
if cur:
if flag:
result.append(cur.val)
else:
stack.append((cur.right, False))
stack.append((cur, True))
stack.append((cur.left, False))
return result前序遍历(根左右)
stack.append((cur.right, False))
stack.append((cur.left, False))
stack.append((cur, True))
后序遍历(左右根)
stack.append((cur, True))
stack.append((cur.right, False))
stack.append((cur.left, False))
二叉树遍历递归模板
中序遍历
# recursively
def inorderTraversal1(self, root):
res = []
self.helper(root, res)
return res
def helper(self, root, res):
if root:
self.helper(root.left, res)
res.append(root.val)
self.helper(root.right, res)前序遍历
# recursively
def inorderTraversal1(self, root):
res = []
self.helper(root, res)
return res
def helper(self, root, res):
if root:
res.append(root.val)
self.helper(root.left, res)
self.helper(root.right, res)后序遍历
# recursively
def inorderTraversal1(self, root):
res = []
self.helper(root, res)
return res
def helper(self, root, res):
if root:
self.helper(root.left, res)
self.helper(root.right, res)
res.append(root.val)