MATLAB(五) 图像处理--图像分割

图像分割

一、基于边界的图像分割

1. 点检测

g = abs(imfilter(tofloat(f), w)) >= T;

f 是输入图像，w 是适合点检测的模板:
，g 是包含检测点的图像。imfilter 把输出转换为输入所属的类，如果输入是整数类，并且 abs 操作不接受整数数据，那么在滤波操作中用 tofloat(f)来防止对数值的过早截取。输出图像 g 是 logical 类；值是 0 和 1。如果 T 值没有给出，那么通常基于滤波结果来选取。在那种情况下，先前的一串指令分成三个基本步骤：1) 计算滤波后的图像 abs(imfilter(tofloat(f),w))；2) 从滤波后的图像的数据中找出 T 的值；3) 把滤波后的图像与T做比较。

---

点检测的另一种方法是在大小为 m×n 的所有邻点中寻找一些点，最大值和最小值的差超出了 T 的值，使用而二维顺序统计滤波器可以完成这个目的：

g = ordfilt2(f, m*n, ones(m, n)) − ordfilt2(f, 1, ones(m, n));
g = g >= T;

2.线检测

g = imfilter(tofloat(f), w);

其中w为线检测模板：

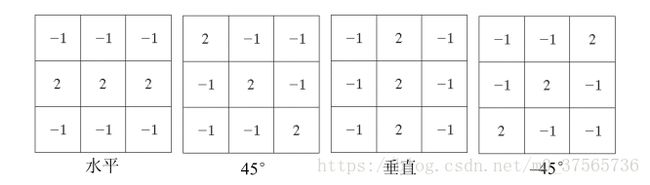
如果图中的第一个模板在图像上移动，就会对水平线(一个像素宽)的响应更强烈。对于恒定的背景，当线通过模板的中间一行时可能产生更大的响应。同样，图 中的第 2 个模板对+45°线响应最好，第 3 个模板对垂直线响应最好，第 4 个模板对
–45°线响应最好。注意，每个模板的优先方向都用比其他可能方向要大的系数加权。每个模板的系数之和为 0，这表明在恒定亮度区域中，模板的响应为 0。若每方向模板都应用于同一图像，其中一方向模板在图像中心点响应比其他模板在图像中心点响应都大，我们就说那个点与模板 i 方向的线更相关。

3.边缘检测

[g，t]=edge(f, 'method', parameters)

f 是输入图像，method 是以下列出方法中的一种，parameters 是下边说明
的附加参数。输出 g 是在 f 中被检测到的边缘点的位置为 1，而在其他地方为 0 的逻辑数组。
参数 t 是可选择的；由 edge 给出阈值，以决定哪个梯度值足够大到可以被称作边缘点。

1. Sobel 边缘检测算子
   Sobel 检测算子的一般调用语法是：

[g,t] = edge(f, 'sobel', T, dir);

其中 f 是输入图像，T 是指定的阈值，dir 是指定的检测边缘的首选方向：’horizontal’、
‘vertical’或’both’(默认值)。
2. Prewitt 边缘检测算子
一般调用语法是：

[g,t] = edge(f, 'prewitt', T, dir);

这个函数的参数和 Sobel 参数相同。Prewitt 检测算子相比 Sobel 检测算子在计算上要简单
一点，但是比较容易产生噪声。
3. Roberts 边缘检测算子
一般调用语法是：

[g,t] = edge(f, 'roberts', T, dir);

这个函数的参数和 Sobel 参数相同。Roberts 检测算子是数字图像处理中最古老的边缘检测
算子中的一种，并且也是最简单的一种。因为在部分功能上有限制，所以这
种检测算子的使用明显少于其他几种算子(比如，Roberts 检测算子是非对称的，而且不能检测
诸如 45°倍数的边缘)。然而，在简单和速度为主导因素的情况下，Roberts 检测算子还是经常
用在硬件实现方面。
4. LoG 检测算子
LoG 检测算子的一般调用语法是：

[g,t ]= edge(f, 'log', T, sigma);

其中的 sigma 是标准差，其他参数和前边解释过的一样。sigma 的默认值是 2。和以前一
样，edge 忽略一切不比 T 强的边缘。如果 T 值没有给出或为空[ ]，edge 会自动选值。将 T
设置为 0，将产生封闭的轮廓，这是我们熟知的 LoG 方法的典型特征。
5. 零交叉检测算子
这种检测算子基于的概念与 LoG 方法相同，但是卷积使用特殊的滤波函数 H 来完成，调用
语法为：

[g,t] = edge(f, 'zerocross', T, H);

其他参数和 LoG 解释的一样。
6. Canny 检测算子
Canny检测算子(Canny[1986])是 edge 函数中最强的边缘检测算子。Canny检测算子的语法是：

[g,t] = edge(f, 'canny', T, sigma);

在这里，T 是向量。T=[T 1 ，T 2 ]，包含在前边步骤 3)的两个阈值，sigma 是平滑滤波器的
标准差。如果 t 包括在输出参量中，t 就是二元矢量，其中包含该算法用到的两个阈值。语法
中的其余参数和其他方法中解释的一样，包括：如果 T 没有指定，就自动计算阈值。sigma 的
默认值是 1。
7.可用边缘检测算子汇总

边缘检测算子	描 述
Sobel	近似导数寻找边缘
Prewitt	近似导数寻找边缘
Roberts	近似导数寻找边缘
LoG	在使用高斯滤波器的拉普拉斯滤波 f(x,y)后，通过寻找零交叉来发现边缘
零交叉	用指定的滤波器滤波 f(x,y)之后，寻找零交叉以发现边缘
Canny	通过寻找 f(x,y)的梯度的局部最大值来发现边缘。梯度由高斯滤波器的微分来计算。该方法使用两个阈值检测强的和弱的边缘，如果它们被连接到强边缘，那么在输出中只包含弱边缘。因此，这种方法更适合用于检测真实的弱边缘

二、基于区域的图像分割

1.区域生长

2.区域分离和聚合

1.四叉树分解
2.四叉树分解中的块值
3.在四叉树分解中设置块值

3.分水岭分割

1.使用距离变换的分水岭分割

• 距离变换

  D = bwdist(BW);

  二值图像的距离变换是指从每个像素到最接近零值的像素的距离。

  • 测地距离变换
    

    D = bwdistgeodesic(BW,mask);

  2.使用梯度的分水岭分割
  获取梯度图像：

h = fspecial('sobel');
fd = tofloat(f);
g = sqrt(imfilter(fd, h, 'replicate') .^ 2 + ...
imfilter(fd, h', 'replicate') .^ 2);

在使用针对分割的分水岭变换之前，常常使用梯度幅度对图像进行预处理。梯度幅度图像沿着物体的边缘有较高的像素值，而在其他地方则有较低的像素值。在理想的情况下，分水岭变换可得到沿物体边缘的分水岭脊线。若梯度图像直接进行分水岭变换可能会严重过分割，所以在计算分水岭变换之前可以先平滑梯度图像。

3.控制标记符的分水岭分割

• 计算局部极小值区域

rm = imregionalmin(f);

其中，f 是灰度图像，rm 是二值图像，rm 的前景像素标记出局部小区域的位置。

• 扩展极小值

im = imextendedmin(f,h);

其中，f 是灰度图像，h 是高度阈值，im 是一幅二值图像，im 的前景像素标记了深的局部小区域的位置。

• 强制最小

mp = imimposemin(f, mask);

其中，f 是灰度图像，mask 是二值图像，mask 的前景像素标记了输出图像 mp 中局部最小区域的期望位置。通过在内部和外部标记符的位置覆盖局部最小区域，可以改进梯度图像.

---

用于控制过分割的一种方法是基于标记符的概念。标记符是属于一幅图像的连通分量。我们希望有一个内部标记符集合，它们处在每个感兴趣物体的内部，而外部标记符集合包含在背景中。

---

标记符的选择范围可以从简单过程到更复杂的方法，涉及尺寸、形状、位置、相对距离、纹理内容等等(见第 11 章中关于描述子的内容)。指针是携带对分割有影响的先验知识的标记符。人们常常使用先验知识在每天的视觉中帮助解决分割和高级任务。最为熟悉的便是使用文本。因此，分水岭分割提供可以有效利用这些类型的知识的框架这一事实，是这一方法的突出优点。

%基于控制标记符的分水岭分割
[file,filepath]=uigetfile('*');
file=fullfile(filepath,file);
img=imread(file);%读图
imgsize=size(img);
if(numel(imgsize)>2)
i=rgb2gray(img);
else
i=img;
end;
imshow(i);title('灰度图');
pause;
%取阈值
[T,SM]=graythresh(i);
bw=im2bw(i,T);
imshow(bw);title('二值');
pause;
% % %%%%%%%%%%%%%%%%%%%%%%%%%%基于距离变换的分水岭分割%%%%%%%%%%%%%%%%%%%%%%
gc = ~bw;
% imshow(gc);
% pause;
D = bwdist(gc);
% figure,contour(-D,40);
imshow(-D,[]);title('距离变换图');
pause;

rm = imregionalmin(-D);%查看局部极小值区域
imshow(rm);title('查看局部极小值区域');
pause;

im = imextendedmin(-D,2);%扩展最小值
% figure,contour(im,40);
fim=i;
fim(im) = -255;
imshow(fim);title('合并后的局部极小值');%查看合并后的局部极小值
pause;

Lim = watershed(bwdist(im));
imshow(Lim,[]);title('基于距离变换的流域分割');
pause;
em = Lim == 0;
res=em|im;
imshow(res);%查看掩膜图像
title('掩膜图像');
pause;


g2 = imimposemin(i, im | em);
imshow(g2);
title('强制最小');
pause;

L2 = watershed(g2);
f2 = img;
f2(L2 == 0) = 255;
imshow(f2);
title('基于控制标记符的分水岭分割');

三、阈值分割

1.使用Otsu方法进行全局阈值分割

level = graythresh(I);

计算全局阈值，level可用于imbinarize将强度图像转换为二值图像。该graythresh函数使用Otsu方法，该方法使用最大类间方差法来计算阈值。

2.使用Otsu方法进行全局直方图阈值分割

T = otsuthresh(counts);

T是由直方图计数计算出的全局阈值，T是一个位于[0,1]范围内归一化强度值，可用于将强度图像转换为二值图像。

3.使用Otsu方法进行多级图像阈值分割

thresh = multithresh(A);

使用最大类间方差法返回一组阈值。你可以将thresh作为imquantize的输入参数，把图像转为二级图像。

4.使用边缘改进全局阈值处理

5.基于局部统计的可变阈值处理

T = adaptthresh(I)；

6.使用移动平均的图像阈值处理

四、霍夫变换

1.霍夫变换

函数 hough 支持任意的默认语法：

[H, theta, rho] = hough(f);

还支持完整的语法形式：

[H, theta, rho] = hough(f, 'ThetaRes', val1, 'RhoRes', val2);

其中，H 是霍夫变换矩阵，theta(以度计)和 rho 是 ρ 和 θ 值向量，在这些值上产生霍夫变换。输入 f 是二值图像，val1 是 0 到 90 的标量，指定了沿 θ 轴霍夫变换的间距(默认是 1)，val2 是 0

2.寻找霍夫变换的峰值

函数 houghpeaks 用任意默认语法
来寻找指定的峰值数：
peaks = houghpeaks(H, NumPeaks)
或者使用完整的语法形式：
peaks = houghpeaks(…, ‘Threshold’, val1, ‘NHoodSize’, val2)
其中，“…”指出来自默认语法和 peaks 的输入是持有峰值行和列坐标的 Q×2 大小的矩阵。Q 的范围是 0 到 NumPeaks，H 是霍夫变换矩阵。参数 val1 是非负的标量，指定了 H 中的什么值被考虑为峰值；val1 可以从 0 到 Inf 变化，默认值是 0.5*max(H(:))。参数 val2是奇整数的两元素矢量，指定量围绕峰值的邻域大小。当鉴别出峰值之后，邻域中的元素被置为 0。默认是由最小奇数值组成的两元素矢量大于或等于 size(H)/50。

3.提取线段

一旦一组候选的峰值在霍夫变换中被识别出来，如果存在与这些峰值相关的有意义的线段，剩下的就是决定线的起始点和终点。函数 houghlines 用默认的语法执行这个任务：

lines = houghlines(f, theta, rho, peaks);

或者使用完整的语法形式：

lines = houghlines(..., 'FillGap', val1, 'MinLength', val2);

其中，theta 和 rho 是来自函数 hough 的输出，peaks 是函数 houghpeaks 的输出。
输出 lines 是结构数组，长度等于找到的线段数。结构中的每个元素可以看成一条线，并含有下列字段：

• point1：两元素向量[r1, c1]，指定了线段终点的行列坐标。
• point2：两元素向量[r2, c2]，指定了线段其他终点的行列坐标。
• theta：与线相关的霍夫变换的以度计量的角度。
• rho：与线相关的霍夫变换的 ρ 轴位置。

其他参数如下：
val1 是正的标量，指定了与相同的霍夫变换相关的两条线段的距离。当两条线段之间的距离小于指定的值时，函数 houghlines 把线段合并为一条线段(默认的距离是 20 个像素)。参数 val2 是正的标量，指定合并的线是保留还是丢弃。如果合并的线比 val2 指定的值短，就丢弃(默认值是 40)。