动态规划法之最长公共子串和最优二叉查找树
1. 笔试常考的题型,最长公共子串问题:给定两个字符串str1和str2,返回两个字符串的最长公共子串(连续)和长度。
举例: str1 = "abc" str2="caba" 它们的最长公共子串是 "ab"。
此题可用暴力法进行求解,求解的时间复杂度较高。现用动态规划法进行求解。
思想:如果 str1 的长度为 n,str2 的长度为 m,生成大小为 n*m 的 数组矩阵 dp , dp[i][j]表示 str1[0…i] 与 str2[0…j] 的
最长公共子串的长度。
计算dp[i][j] 的方法一如下:
1)矩阵 dp 的第一列 dp[0…m-1][0].对于 某个位置(i,0)如果str1[i]==str2[0],则dp[i][0]=1,否则dp[i][0]=0
2)矩阵 dp 的第一行 dp[0][0…n-1].对于 某个位置(0,j)如果str1[0]==str2[j],则dp[0][j]=1,否则dp[0][j]=0
3)其他位置从左到右从上到下计算,dp[i][j]的值只有两种情况:
当str1[i]==str2[j]时,dp[i][j]=dp[i-1][j-1]+1;
当str1[i]!=str2[j]则dp[i][j]=0。
图示如下:
Java代码实现,请参考getMaxSubString1()。
解法二:经典动态规划的方法需要大小为m*n的 dp 矩阵,空间复杂度可以减少至O(1),因为计算每一个dp[i][j]时只需计算dp[i-1][j-1],按照斜线方向计算所有的值,只需要一个变量即可。Java代码实现,请参考getMaxSubString2()。
package ExamTest;
/*用例:
abcdefghi bcdabefghijk
结果:
方法一:efghi
5
方法二:efghi
5
*/
import java.util.Scanner;
public class MaxSubString
{
public static void main(String[] args)
{
Scanner reader = new Scanner(System.in);
String str = reader.nextLine();
String[] strs = str.split(" ");
String strs1 = strs[0];
String strs2 = strs[1];
char[] str1 = strs1.toCharArray();
char[] str2 = strs2.toCharArray();
getMaxSubString1(str1,str2);
getMaxSubString2(str1,str2);
}
public static void getMaxSubString1(char[] str1,char[] str2)
{
int dp[][]=new int[str2.length][str1.length];
//对dp矩阵的第一行赋值
for(int i=0;i 0) //如果这一列有元素没有比对完成,本列继续往前判断.
{
col--;
}
else //一列比对完成,下移一行
{
row++;
}
}
System.out.println(max);
}
} 2. 最优二叉查找树(动态规划法)
问题引入及描述:
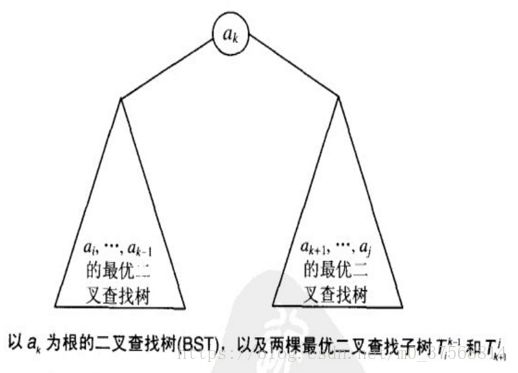
•在计算机科学中,二叉查找树是最重要的数据结构之一。它的一种最主要应用是实现字典,这是一种具有查找、插入和删除操作的元素集合。如果集合中元素的查找概率已知,这就很自然地引出了一个最优二叉查找树(BST)的问题:它在查找中的平均键值比较次数是最低的。
•n个键{a1,a2,a3......an},其相应的查找概率为{p1,p2,p3......pn}。构成最优BST,表示为T1n ,求这棵树的平均查找次数C[1, n](耗费最低)。即:如何构造这棵最优BST,使得C[1, n] 最小。
动态规划求解过程:
•从中选择一个键ak作根节点,它的左子树为T(i)k-1,右子树为T(k+1)j。要求选择的k 使得整棵树的平均查找次数C[i, j]最小。左右子树递归执行此过程。
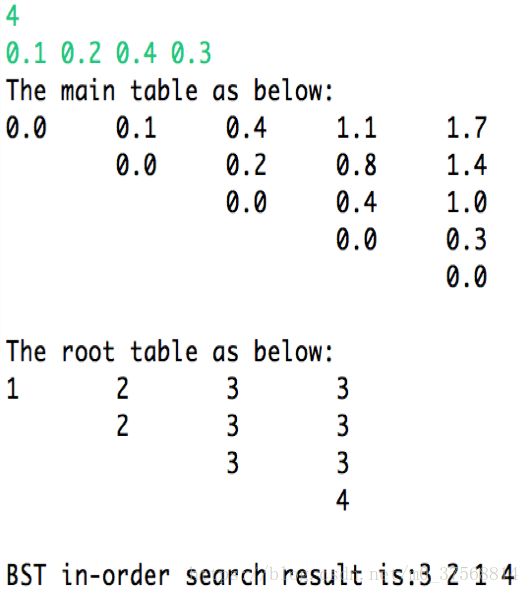
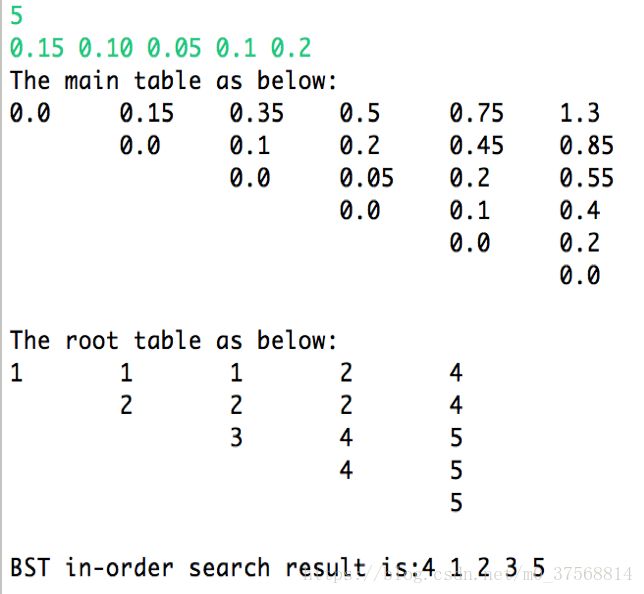
考虑分别以概率0.1,0.2,0.4,0.3来查找4个键A,B,C,D 求成功查找时,最优平均键值比较次数。
Java代码如下:
package ExamTest;
import java.util.Scanner;
/**
* Created by ZhangAnmy on 18/9/15.
* 输入:一个n个键的有序列表的查找概率数组prop[1..n]
* 输出:在最优BST中成功查找的平均比较次数,以及最优BST中子树的根表rTable
*/
public class OptimalBST {
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
int num = sc.nextInt();
float[] prop = new float[num+1];
float[][] cTable = new float[num+2][num+1];
int[][] rTable = new int[num+2][num+1];
for(int i=1;i<=num;i++)
{
prop[i]=sc.nextFloat();
}
optFunc(num,cTable,prop,rTable);//调用动态规划方法,求最优二叉查找树
print(num,cTable,rTable);//打印主表和最优根表
System.out.print("BST in-order search result is:");
OptimalBSTPrint(1,num,rTable);
}
public static void optFunc(int num,float cTable[][],float prop[],int rTable[][])
{
for(int i=1;i<=num;i++)//主表和根表元素的初始化
{
cTable[i][i-1]=0;
cTable[i][i]=prop[i];
rTable[i][i]=i;
}
cTable[num+1][num]=0;
int d = 0,kmin = -1,k,i,j,s;
float minval=9999,sum=0,temp;
for(d=1;d<=num-1;d++)
{
for(i=1;i<=num-d;i++)
{
j = i+d;
temp=minval;
for(k=i;k<=j;k++)//找最优根
{
if(cTable[i][k-1]+cTable[k+1][j]运行结果: