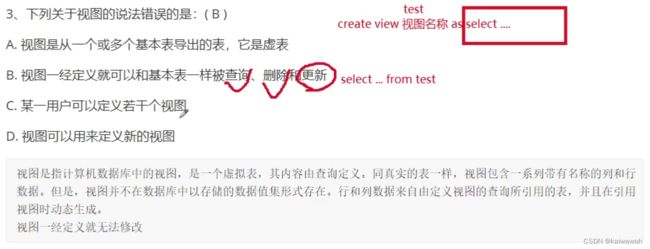
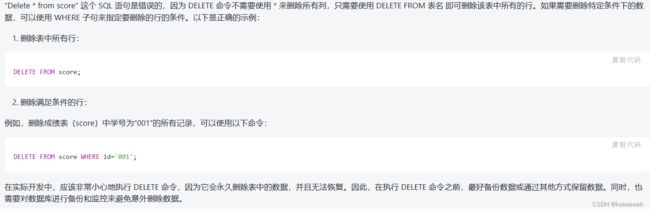
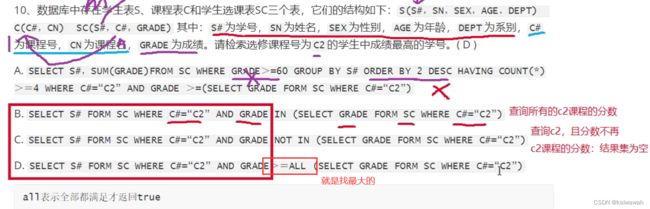
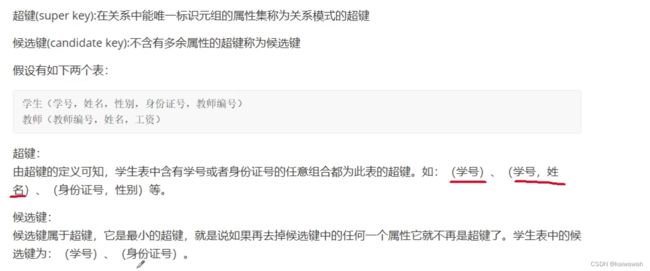
笔试强训 - 错题总结
目录
选择题
基础语法及数据结构相关选择题
编辑
编辑
网络编程相关
数据库相关选择题:
超键、候选键
alter相关知识点
编辑 模糊查询
多线程相关选择题:
编程
编辑
计算糖果
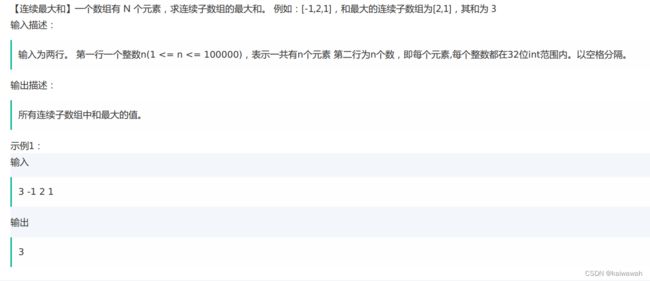
计算连续最大和
判断合法的括号串
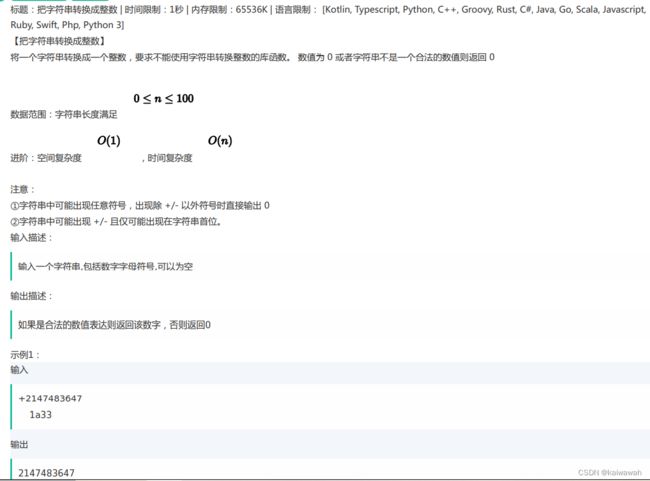
把字符串转成整数
另类加法
走方格的方案数 编辑
参数解析
跳石板
手套
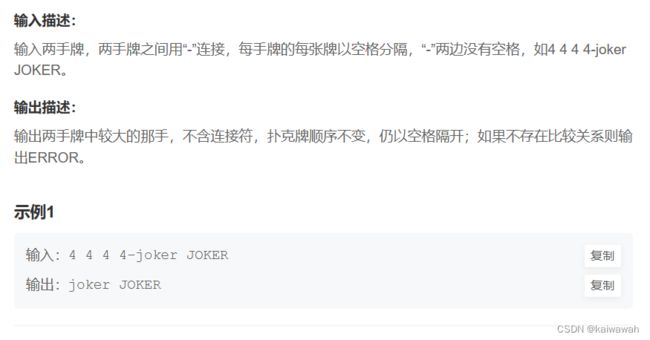
扑克牌大小
查找两个字符串a,b中的最长公共子串
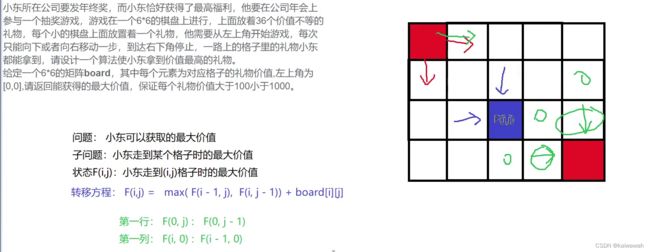
年终奖
星际密码
求正数数组的最小不可组成和
选择题
基础语法及数据结构相关选择题
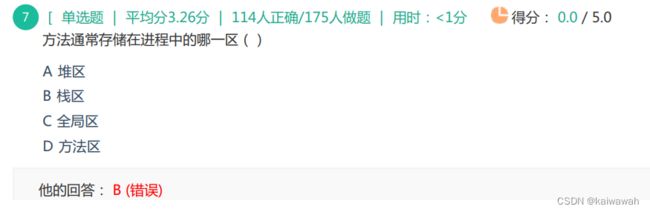
方法在方法区
private 只能让自己访问和修改 子类不行的
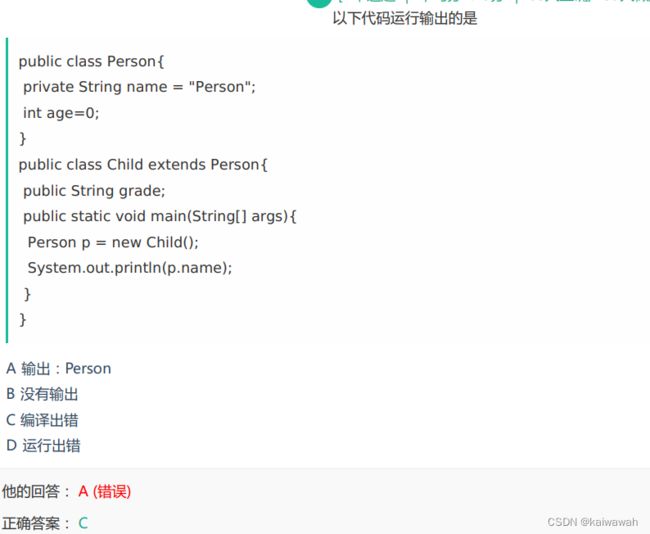
name被private修饰了,类外不能访问
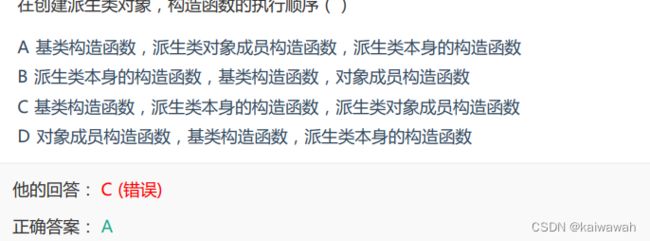
大坑,没有在子类给父类写带参数的构造方法的代码
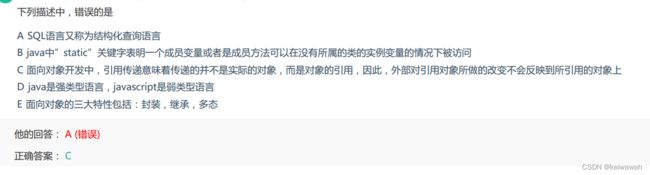
外部引用对象所做的改变可以反映到对象本身上
不如说一个方法 让其数组arr【0】 = 10;
![]()
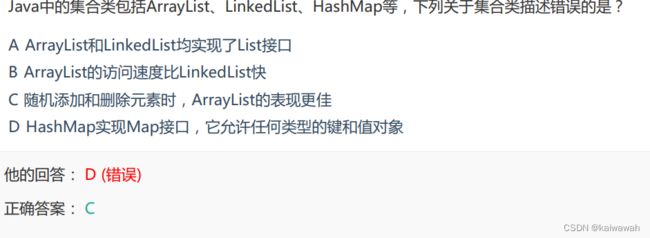
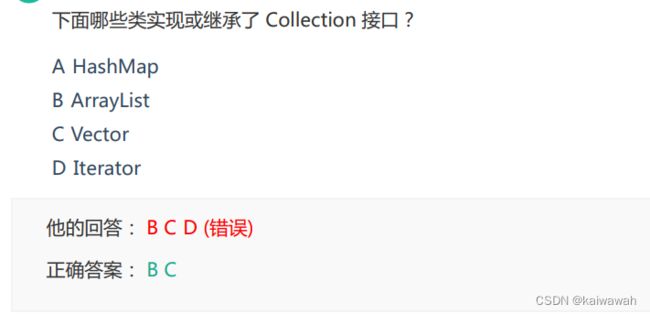
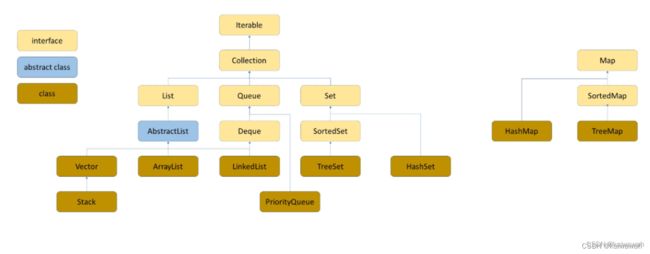
A是正确的 可以将null用作 键或值
参照下图
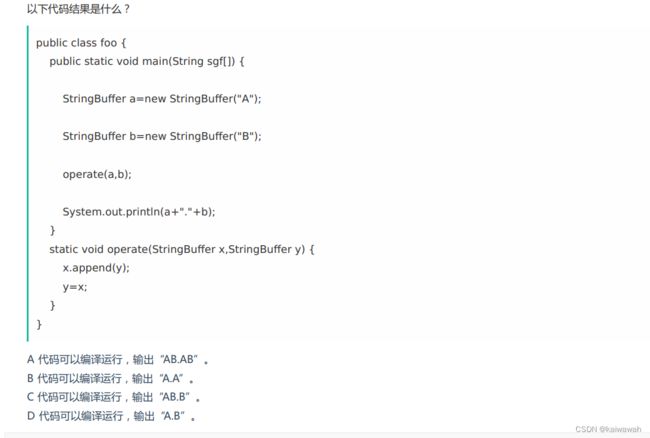
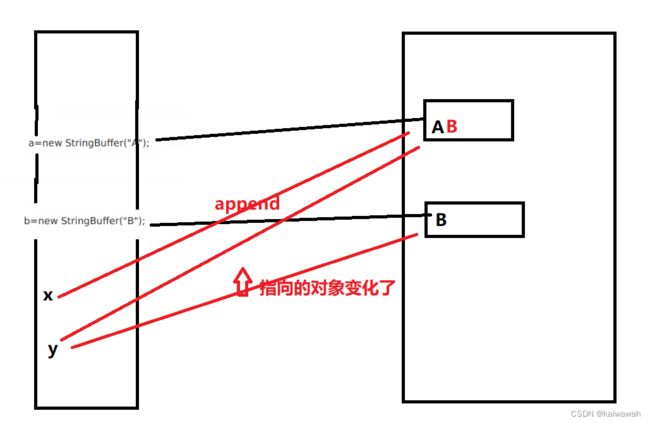
这里我们要明确 值传递,引用传递
值传递:是指在调用函数时将实际参数复制一份传递到函数中,这样在函数中如果对参数进行修改,将不会影响到实际参数。
引用传递:是指在调用函数时将实际参数的地址直接传递到函数中,那么在函数中对参数所进行的修改,将影响到实际参数。
这里的operate里 x.append 对于x所指向的对象 将其发生改变 因此 a的值发生了改变 ,但是y 只是将指向对象 变为了x所指向的对象~~
浅浅画个图吧
方法不是继承 是不能被覆盖
这里的finally语句 如果有return的话 会覆盖之前的return
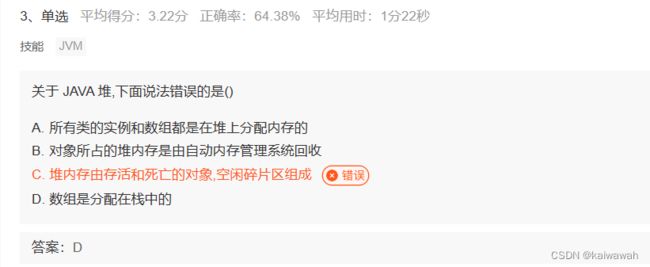
栈里面存的是各类方法的调用关系,而堆存的可以理解为new出来的万物都存在了堆内,因为数组是 形如“int[] n = new int[10]”这样的形式,因此数组分配到堆中。
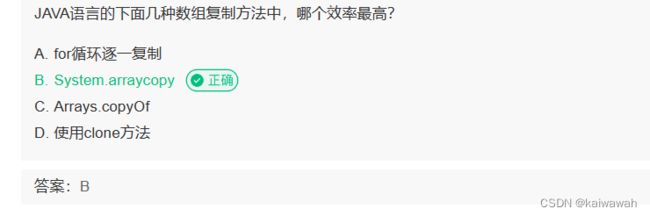
System.arraycopy是浅拷贝,相对于拷贝了一个对象引用,而不是真正意义上的拷贝,因此效率最高
通过看Arrays.copyOf源码: 很明显的看到System.arraycopy明显效率高于copyOf的 再看clone方法,clone方法比较特殊,对于对象拷贝是深拷贝,而对于数组的拷贝是浅拷贝 四个的效率高低进行排序
很明显的看到System.arraycopy明显效率高于copyOf的 再看clone方法,clone方法比较特殊,对于对象拷贝是深拷贝,而对于数组的拷贝是浅拷贝 四个的效率高低进行排序
System.arraycopy > Arrays.copyOf > clone > for
需要再Employee 构造方法内要spuer~~
==比较值,在比较的时候 j自动拆箱 自动变成int的0,第一个就是true,第二个的话还需要看一下源码
因为j会自动拆箱 所以在比较的时候,就是int 值 与 int 值进行比较。
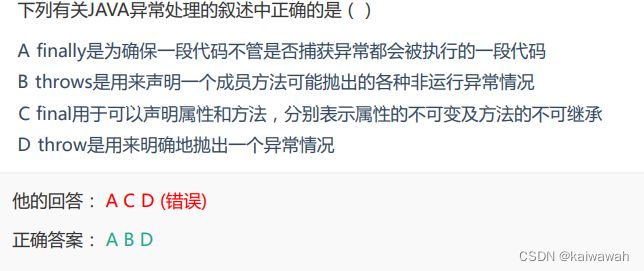
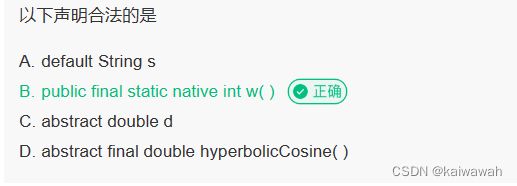
A选项defalut不能修饰变量,C选项一样,D选项的话 加上final的方法不能被覆盖(重写)的,又因为前面时abstract说明时抽象方法,因此D是错误的
a是类A的一个属性(全局变量) ,当我们new这个实例的时候,a是存在堆区的,而b和c都是方法内的,就是在栈里的。
 在+运算符进行相加的时候,byte类型会自动变成int 结果也是int 但是b4b5是final修饰了,这个结果并不会变成int 而下面的b1+b2就会编译报错了
在+运算符进行相加的时候,byte类型会自动变成int 结果也是int 但是b4b5是final修饰了,这个结果并不会变成int 而下面的b1+b2就会编译报错了
ACD选项都不是检查型异常,不需要特别声明而C是检查型异常 需要编写程序时声明
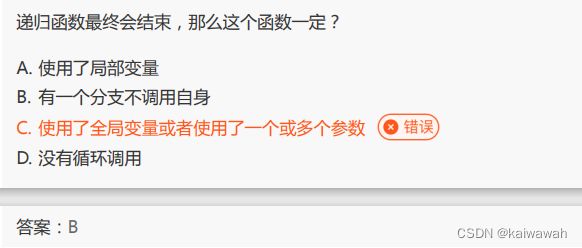
关于递归的结束基本上就是有一个判断条件进行return;类似的操作,这个操作就是该分支不调用自身,因此答案是B。
这种题先看后序遍历的最后一个是a,那么根子树是a 再看中序遍历 以a为界限,左部分是左子树,右部分是右子树(a的) 。a看完再看d,在中序遍历序列中,以d为界限,左子树是空,右子树是efcg.....以此类推~~
栈的LIFO功能就符合这种记忆性的功能~~
![]()
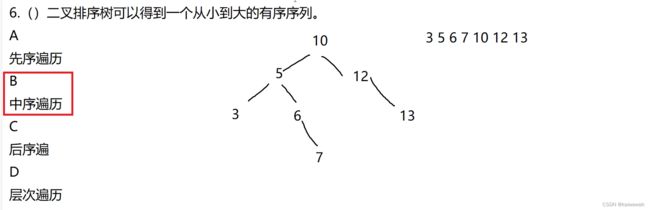
做题的时候 记混了 应该是中序遍历结果是有序序列,下次做题可以多使用例子来证明~~
此题思路就是看 有几个元素到达最终位置就是第几趟排序~~
在JVM内存中:程序计数器、栈区是线程隔离的,方法区和堆区是线程之间共享的~~
D选项因为JVM也是有版本区分的,不同版本可能会出现无法正常运行的现象。
正常的线程启动需要在main方法里有调用start方法 ,但是如果没有这个调用方法的话,这里的 run就是普普通通的在main方法内调用了run方法,不会出现抢占式调度的现象。
接口中的变量都是全局常量
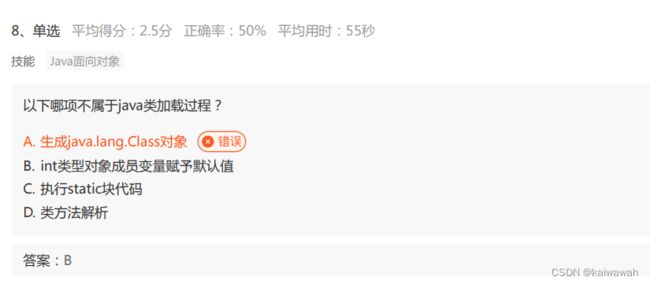
错的原因是 看错了。。 这里的题意是不属于类加载 那就选B了。
 操作系统
操作系统 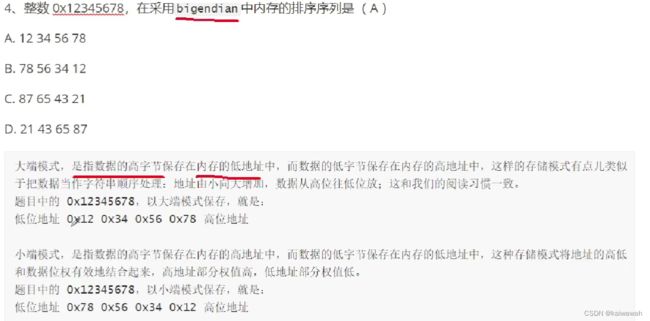
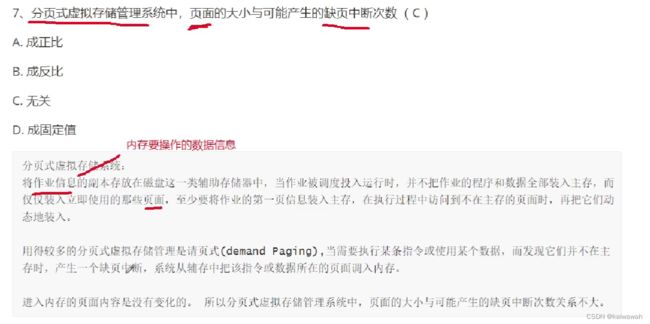
在这里我们可以这样理解,我们将信息分为很多页 ,我们用到那一页的数据再把那一页提取到主存使用就ok了,如果出现了缺页中断,和页面大小 是没有关系的,就好比你看书的时候,发现缺页了,缺页的发生和你纸张大小有关系吗?
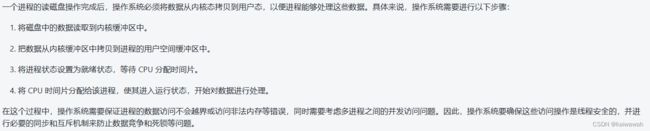
操作系统的主要功能包括处理机管理、存储器管理、设备管理和文件管理,其中处理机管理指的是对 CPU 的管理,包括进程调度、死锁处理等;存储器管理指的是对内存的管理,包括地址映射、内存分配和回收等;设备管理指的是对各种输入输出设备(如鼠标、键盘、打印机)的管理,包括设备驱动、设备分配和回收、设备中断处理等;文件管理指的是对磁盘上的文件进行管理,包括文件存储、文件读写、文件保护和备份等。可移植性不是操作系统的主要功能,但是在操作系统设计时通常会考虑到其可移植性,以便能够运行于不同的硬件平台和操作环境中。
网络编程相关
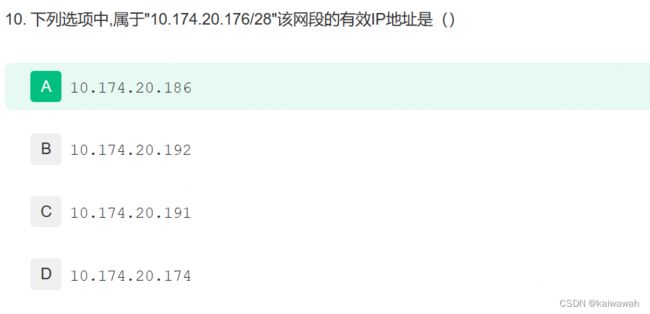
在IP地址的表示方法中,IPv4地址是32位的二进制数,一般用点分十进制表示法进行显示和输入。例如,"10.174.20.176"是一个IPv4地址。其中每个数都在0到255之间,表示该IP地址的前三个数字(10.174.20)是网络部分,最后一个数字(176)是主机部分。
在IPv4地址划分时,为了更好地管理计算机和设备,通常采用子网掩码将IP地址划分成多个子网。子网掩码是一个32位的二进制数,其作用是表明IP地址中哪些位是网络位,哪些位是主机位。子网掩码的值可以通过CIDR(无类域间路由)记号进行表示,CIDR记号的格式是IP地址加上一个斜线再加上一个数字,如"10.174.20.176/28"。其中,"/28"表示该IP地址所属的子网掩码包括前28个二进制位为网络位。
对于"10.174.20.176/28"这个例子,其子网掩码的二进制表现应该是"11111111.11111111.11111111.11110000",转换为十进制表示则是"255.255.255.240"。这意味着在该IP地址段中,前28个二进制位是网络位,后4个二进制位是主机位。由于有4个二进制位用于表示主机位,因此可用IP地址数量为2^4(即16个)。
需要注意的是,每个IP地址段都有一个网络地址和一个广播地址。在"10.174.20.176/28"中,网络地址是"10.174.20.176",广播地址是"10.174.20.191",这两个地址不可分配给设备使用,因此可用IP地址数量为16-2=14个。
数据库相关选择题:
数据库系统的特点:数据冗余度低、数据具有完整性、数据共享性好、数据的独立性高
答案是A。
多对多联系在关系模型中通常是通过建立新的关系来实现的。具体来说,如果在实体-联系模型中两个实体之间有一条多对多联系,就需要建立一个新的关系表,该表包含这两个实体的主键作为外键。例如,在一个电影租赁系统中,用户可以租任意数量的电影,而每部电影也可以被多个用户租借。在这种情况下,需要建立一个新的关系表来跟踪租借记录,该表包含用户ID和电影ID作为外键。这样就可以通过连接三个表来获取用户租借的所有电影或特定电影租借的所有用户。
可以这样理解:在数据库中,我们通常使用关系模型来组织数据。为了将实体-联系模型转换为关系模型,我们需要将所有实体和联系都转化为表的形式。对于实体而言,每个实体对应一个表;对于联系,如果是一对一或一对多的联系,可以通过在某张表中添加相应的字段来实现;而对于多对多的联系,则需要新建一个表来存储它们之间的关联。
再来举一个实际例子。假设我们要设计一个简单的图书管理系统,其中包含三个实体:图书、作者和出版社。每本图书可以有多个作者,每个作者可能著有多本书,每本书只属于一个出版社。这时,我们需要将这些实体转换为关系模型。
首先,我们可以将每个实体转化为一个表。例如,图书表(book table)、作者表(author table)和出版社表(publisher table)。每个表都包含若干个字段,用来存储相应实体的属性信息。例如,在图书表中,可能会包含以下字段:书名、ISBN、价格等等。在作者表中,可能会包含以下字段:姓名、国籍、生日等等。在出版社表中,可能会包含以下字段:名称、地址、联系方式等等。
接下来,我们需要解决多对多的问题。因为一本书可以有多个作者,一个作者也可能著有多本书,所以它们之间存在多对多的关系。我们可以通过一个新的表(例如,图书-作者关系表 book_author table)来存储这些关系。该表包含两个外键,分别指向图书表和作者表,用来表示两者之间的关联关系。
最后,我们需要解决一对多的关系。因为一家出版社可以出版多本书,所以它们之间存在一对多的关系。在图书表中,我们可以添加一个外键,指向出版社表中的出版社ID字段,用来表示这种关系。
这样,我们就成功将实体-联系模型转换为了关系模型,并可以使用SQL语句对其进行操作。例如,如果需要查询某个作者著作的所有书籍,只需要在作者表和图书表之间连接图书-作者关系表并过滤作者ID即可。
第一范式(1NF)是关系数据库设计中的基本概念,要求关系表的所有属性值必须是不可分的原子值,不能存在重复的属性或属性组。
第二范式(2NF)是进一步规范化关系数据库设计的概念,要求关系表中的每个非主键属性都必须完全依赖于主键,而不能部分依赖于主键或者依赖于主键的一部分。
第三范式(3NF)是在1NF和2NF的基础上,进一步规范化关系数据库设计的概念,要求关系表中的每个非主键属性都不依赖于其它非主键属性,即不存在传递依赖关系
举个例子,假设有一个订单管理系统,其中有一个订单信息表 Order,包含下面这些字段:
- OrderId(主键)
- CustomerName
- CustomerPhone
- ProductName
- ProductPrice
- Quantity
- TotalPrice
如果我们对该表进行第三范式的规范化,则需要将其中存在传递依赖关系的字段拆分出来。具体来说,可以将上述订单信息表拆分为三张表:
- Order(OrderId, CustomerId, ProductId, Quantity, TotalPrice)
- Customer(CustomerId, CustomerName, CustomerPhone)
- Product(ProductId, ProductName, ProductPrice)
在这种情况下,每张表都符合第三范式的要求:
- Order 表中只包含 OrderId、CustomerId、ProductId、Quantity 和 TotalPrice 这几个字段,而不是把 CustomerName、CustomerPhone、ProductName 和 ProductPrice 也存储在该表中。
- Customer 和 Product 表中只包含本身相关的字段,并不涉及其它表的信息。
这样的设计符合了第三范式的规范化要求,避免了数据冗余和更新异常的问题。
假设有一个学校的学生选课系统,其中有两个表:学生信息表(Student),包含学生编号(StudentId)和学生姓名(StudentName),以及选课信息表(CourseSelection),包含学生编号(StudentId)、课程编号(CourseId)和成绩(Grade)这三个字段。
如果我们对该数据库进行第二范式的规范化,则需要将表中存在部分依赖关系的字段进行拆分。具体来说,可以将上述两个表拆分为三张表:
- Student(StudentId, StudentName)
- Course(CourseId, CourseName)
- CourseSelection(StudentId, CourseId, Grade)
在这种情况下,每张表都符合第二范式的要求:
- 在 Student 表中,每个字段都完全依赖于主键 StudentId。
- 在 Course 表中,每个字段都完全依赖于主键 CourseId。
- 在 CourseSelection 表中,每个非主键字段都完全依赖于主键 (StudentId, CourseId)。
这样的设计符合了第二范式的规范化要求,避免了数据冗余和更新异常的问题。
假设有一个订单数据库,其中有一个 Order 表,包含订单编号(OrderId)、客户编号(CustomerId)、客户姓名(CustomerName)、客户地址(CustomerAddress)和产品名称(ProductName)这五个字段。
在这个表中,存在以下两个问题:
- 部分依赖:客户编号、客户姓名和客户地址这三个字段都依赖于订单编号,而不是依赖于客户编号。
- 传递依赖:产品名称依赖于客户编号,间接依赖于订单编号。
为了符合第二范式,我们需要将该订单表拆分成两个表:
- Order(OrderId, CustomerId, ProductName)
- Customer(CustomerId, CustomerName, CustomerAddress)
在这种设计下,每个表都符合第二范式的要求:
- 在 Order 表中,每个非主键字段都完全依赖于主键 OrderId。
- 在 Customer 表中,每个非主键字段都完全依赖于主键 CustomerId。
但是在这个设计中,仍然存在着传递依赖的问题:对于 Customer 表的订单编号与产品名称没有直接关系,却依赖于 CustomerId。为了符合第三范式的要求,我们可以将 Order 表再次拆分,得到三个表如下:
- Order(OrderId, CustomerId)
- Product(ProductId, ProductName)
- OrderItem(OrderId, ProductId)
在这个设计下,每个表都符合第三范式的要求:
- 在 Order 表中,每个非主键字段都完全依赖于主键 OrderId。
- 在 Product 表中,每个非主键字段都完全依赖于主键 ProductId。
- 在 OrderItem 表中,每个非主键字段都完全依赖于主键 (OrderId, ProductId),不存在传递依赖关系。
这样的设计保证了数据表中所有非主键属性都是相互独立的,避免了数据冗余和数据不一致的问题
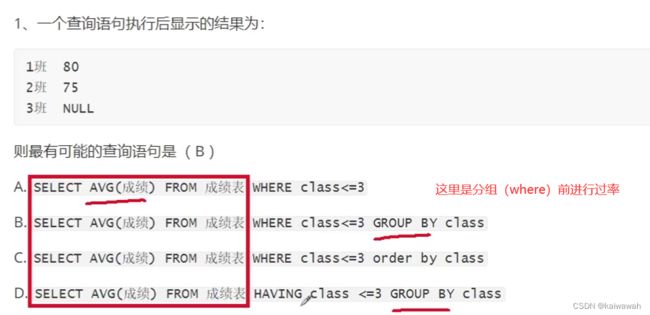
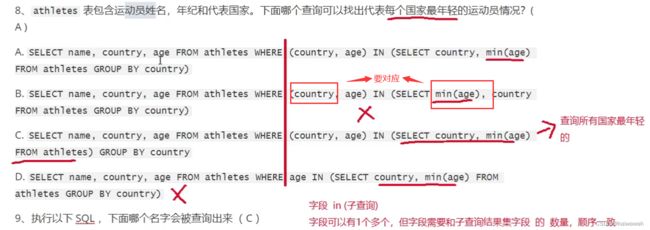
BC选项,在用了聚合函数之后,前面的*和stu-id就是空了,查询不到了
$result这个变量的字段数量 而这个变量求的是id,name,age三个。
c选项是前提是已经使用了sample数据库才是对的,因此选D
引起冲突:换句话说就是会相互影响~~
D选项都是select就不会影响,但如果是其他的呢?
E选项先删了 再改就不能改了
F可以 第二次删除同一个数据 会成功,但是没删除任何数据。
UDP协议是不可靠传输,不满足MySQL服务器的要求的。
超键、候选键
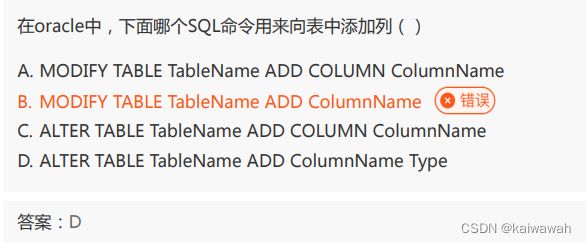
alter相关知识点
数据库索引(Database Index)是一种用于加速数据库查询操作的数据结构。它类似于书籍的目录,可以帮助我们更快地查找到需要的信息,从而提高数据库的检索效率和性能。
在数据库中,索引可以被理解为一个按照特定规则组织的数据结构,它存储了表中某些列的值和对应的行指针,用于支持快速的数据查询操作。当我们在执行 SQL 查询语句时,数据库会首先搜索索引来获取符合条件的记录的行指针,然后再利用这些行指针查找实际的数据行。相比于全表扫描,使用索引进行查询可以大大减少数据扫描的次数,提高查询的效率。
原子性(Atomicity)是指一个操作或者事务是不可分割的单位,要么全部执行成功,要么全部执行失败回滚。在数据库中,事务是一个原子性的操作单元。当一个事务包含多个操作时,这些操作要么都成功提交,要么都失败回滚。也就是说,事务中的所有操作要么全部完成,要么全部撤销,不会只完成其中一部分操作。
隔离性(Isolation)是指在一个事务执行的过程中,该事务所做的修改在最终提交之前,对其他事务是不可见的。也就是说,当一个事务正在修改数据时,其他并发事务不能访问同一数据,只有当前事务提交后,其他事务才能看到修改后的数据。这样可以避免并发事务之间的冲突和数据不一致。
一致性(Consistency)是指数据库在执行事务前后,都必须保持数据的一致性。也就是说,事务操作的结果必须使数据库从一种正确的状态变成另一种正确的状态。如果一个事务操作前后,数据不满足某些约束条件,则该事务应该被回滚,恢复到操作前的状态。
持久性简单来说就是将数据存到了硬盘中,永久保持~~
 模糊查询
模糊查询
多线程相关选择题:
重复读(Repeatable Read)是数据库的一种事务隔离级别,它保证在同一个事务中多次读取同一数据时能够得到相同的结果,即保证了在同一个事务内,多个查询操作返回的数据集合是一致的。这意味着如果在一个事务中对同一条记录进行了多次读取操作(例如 SELECT),那么无论其他事务做出何种修改,这些读取操作都会返回同样的结果。
在重复读隔离级别下,事务开始后会创建一个可重复读的视图,该视图会包括所有在事务开始时间之前已经提交的数据。在此事务中读取数据时,只能访问该视图中的数据,而不能访问其他事务未提交的数据。因此,在重复读隔离级别下,可以防止脏读和不可重复读的问题,但是,在某些情况下可能会出现幻读问题。
需要注意的是,重复读隔离级别可能会导致并发性能下降,因为它在事务期间锁定了读取的数据。同时,由于隔离级别比较高,因此可能存在一些数据竞争的情况,这需要我们根据具体的业务场景选择合适的事务隔离级别,以提高系统性能和数据安全性。
脏读(Dirty Read)是数据库中一种常见的并发问题,指的是在一个事务中读取到了另外一个未提交的事务所写入的数据。当一个事务读取到了其他事务未提交的数据时,如果这些数据随后被撤销或者回滚,那么当前事务所读取的数据就是无效的。
举个例子,假设有两个事务,A 和 B,A 事务执行了一个更新操作但未提交,此时 B 事务读取了 A 事务更新后但尚未提交的数据,接着 A 事务将更新撤销或回滚,此时 B 事务读取的数据就变成了无效的数据,即出现了脏读的情况。
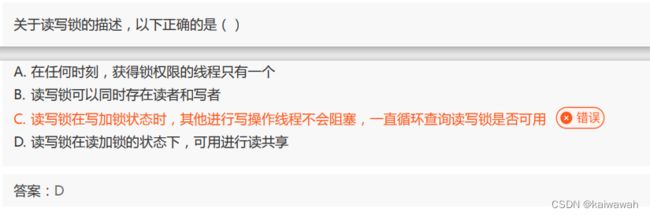
解释一下排它锁:
排他锁(Exclusive Lock),也称为写锁(Write Lock),是数据库中一种常见的锁机制,用于控制对数据的访问权限。当一个事务获取了排他锁后,其他事务将无法同时获取该行数据的排他锁或共享锁,即其他事务无法读取或修改这条数据。排他锁可以保证数据在被修改期间不会被其他事务读取,以防止出现脏读、不可重复读等并发问题。
举个例子,假设有一个数据库表中的一条记录,事务 A 获取了该记录的排他锁,表示事务 A 正在修改该记录,此时其他事务 B 或 C 都无法获取该记录的锁。如果事务 B 也想要获取该记录的排他锁,则需要等待事务 A 释放该锁,否则事务 B 会被阻塞。只有当事务 A 修改完该记录后,释放排他锁,事务 B 才能获得该锁。
需要注意的是,当多个事务对同一数据进行操作时,排他锁可能会导致死锁等并发问题,因此需要谨慎使用。在实际应用中,我们可以根据具体情况选择合适的锁机制来保证数据的安全性和并发性能。
T获取了Q的排它锁,T当然可以任意操作Q了,但是其他事项不能操作Q了。
![]()
B选项的话就是俩个线程互相等待对方锁释放这个情景~~
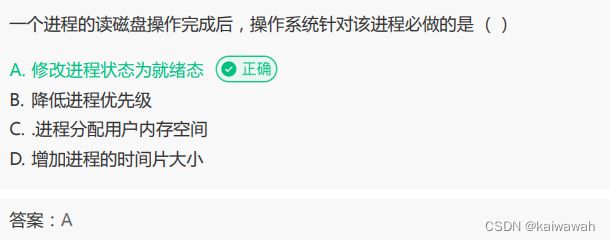
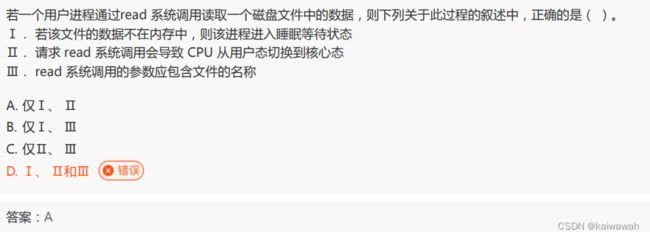
read进程是io读操作,读操作会将数据先从硬盘中读到内存,再从内存读出来的,而硬盘读到内存的时间花费是比较大的,因此为了提高效率,当内存中没文件的数据,那就进入睡眠等待呗~~
Ⅱ. 请求 read 系统调用会导致 CPU 从用户态切换到核心态,以进行系统调用操作。
Ⅲ. read 系统调用的参数应包含文件描述符而非文件名称。
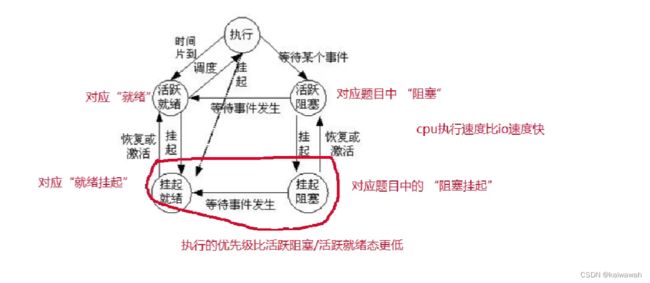
先搞清以下几点:
抢占式/强占式:
一个进程好好的运行,突然来了一个优先级高的线程,这时候正在运行的线程就得让空给优先级高的线程。
静态优先权:
线程创建的时候就已经确定了,不会更改优先级
动态优先权:
随等待时间增长而增长
编程
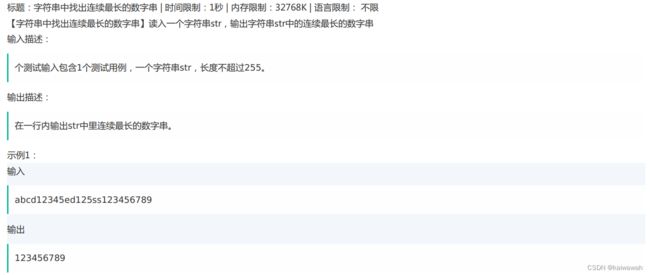
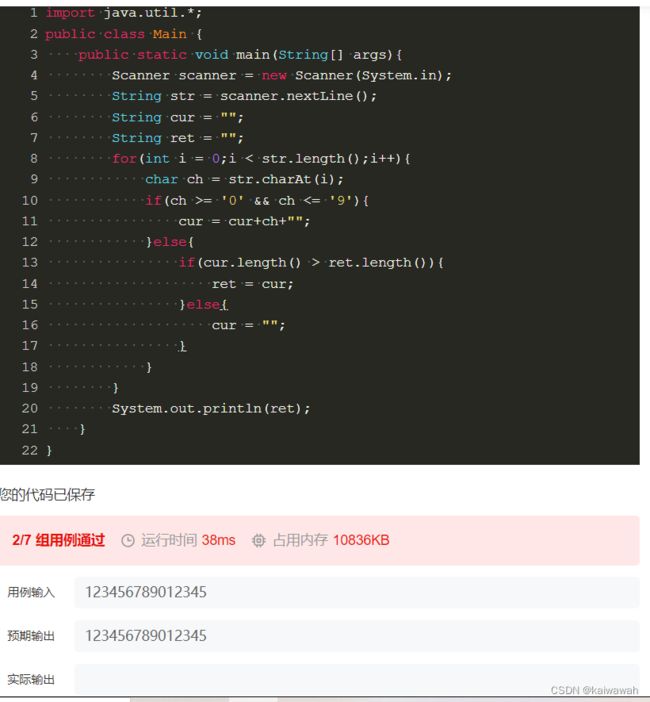
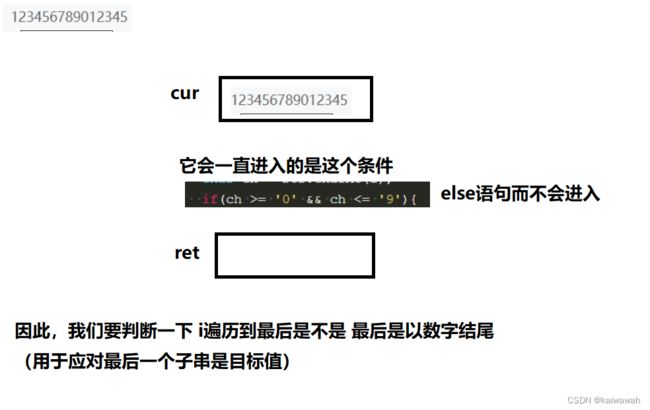
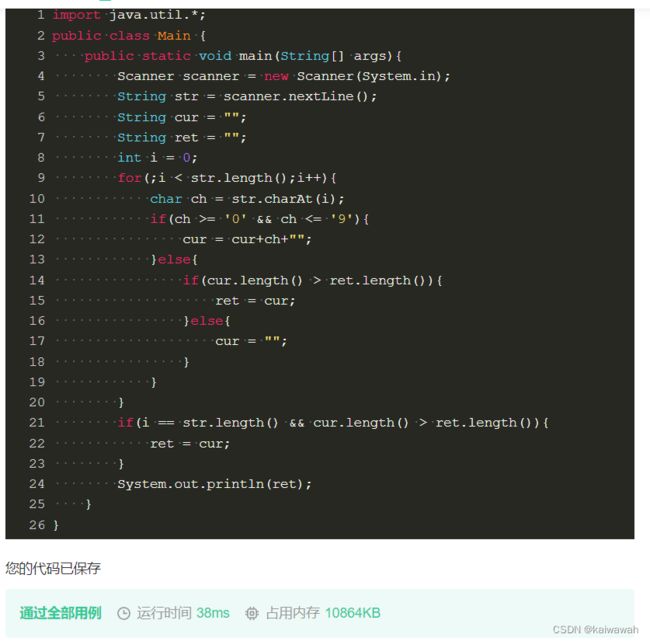
可以这样解:定义俩个String类型 一个为cur 一个ret ret 作为结果 只有是数字就用cur接收,如果遇到字母,就让cur和ret比较长度
为啥还不行呢?
计算糖果
这道题做错 最大的问题是 没考虑到 b有俩种取值~~
计算连续最大和
此题用动态规划思想
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] nums = new int[n];
for(int i = 0;i < nums.length;i++){
nums[i] = scanner.nextInt();
}
int max = nums[0];
int sum = nums[0];
for(int i = 1; i < nums.length;i++){
sum = Math.max(nums[i]+sum,nums[i]);
max = Math.max(sum,max);
}
System.out.println(max);
}
}
判断合法的括号串
import java.util.*;
public class Parenthesis {
public boolean chkParenthesis(String A, int n) {
if(A.isEmpty() || n == 0){
return false;
}
if(n % 2 != 0){
return false;
}
// write code here
Stackstack = new Stack<>();
for(int i = 0;i < n; i++){
char ch = A.charAt(i);
if(ch != '(' && ch != ')'){
return false;
}else if(ch == '('){
stack.add(ch);
}else if(ch == ')'){
if(stack.isEmpty()){
return false;
}
if(stack.peek() == '('){
stack.pop();
}
}
}
if(!stack.isEmpty()){
return false;
}
return true;
}
} 关键是 如果第一个是 )就要判断 这个是不是第一次进入栈的~~
把字符串转成整数
public class Solution {
public int StrToInt(String str) {
if(str.isEmpty()){
return 0;
}
char[] chs = str.toCharArray();
int flg = 1;
int sum = 0;
if(chs[0] == '-'){
flg = -1;
chs[0] = '0';
}
if(chs[0] == '+'){
flg = 1;
chs[0] = '0';
}
for(int i = 0;i < chs.length;i++){
if(chs[i] < '0' || chs[i] > '9'){
sum = 0;
break;
}
sum = sum * 10 + chs[i] - '0';
}
return sum * flg;
}
}另类加法
这个不让用算数运算符的话就直接用位运算:
1.二进制位相异或的结果,是俩个数对应位相加的结果,不考虑进位。
2.二进制与后左移一位的结果,是俩个数相加进位后的结果。(只考虑进位)
关键判断进不进位咯~~
我们可以这样处理:
用sum表示A和B俩个数相异或的结果,carray 为 A和B与后左移一位的结果,得到sum和carray后,看carray是不是为0,如果不为0就让sum变成A,carray变成B进入循环,只要等到carray为0时,输出sum就是结果了。
import java.util.*;
public class UnusualAdd {
public int addAB(int A, int B) {
// write code here
int sum = A ^ B;
int carray = (A & B) << 1;
if(carray == 0){
return sum;
}
return addAB(sum,carray);
}
}走方格的方案数 
先从n,m数比较小的情况来分析入手:
当n == 1 m == 1的时候 左上角到右下角的路径有2条,
当n == 1 m == 3的时候,路径有4条,
当m == 1 n == 3的时候,路径也有4条。
综上所述,当n == 1 或者是 m == 1的时候,路径就是n+m条可供选择。
根据这一块,我们可以不可以利用子问题思想,不断将问题划分,利用递归的方法来实现呢?
就是说先从左上角出发,等到n == 1或者说是m == 1的时候 再返回n+m 就能得到结果了。
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextInt()) { // 注意 while 处理多个 case
int a = in.nextInt();
int b = in.nextInt();
int size = getmed(a,b);
System.out.println(size);
}
}
private static int getmed(int n,int m){
if(n == 1 || m == 1){
return n+m;
}
return getmed(n-1,m)+getmed(n,m-1);
//这里的-1就是向右向下走的过程~~
}
}递归过程如下:
参数解析
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
String str = scan.nextLine();
int count = 0;
for(int i = 0;i跳石板
采用动规思想去做:想想给的示例,如何筛选的如何去判断的
判断约数那里 先判断能不能除尽、在这个条件前提下看另一个约数是不是相同的~~
import java.util.*;
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextInt()) { // 注意 while 处理多个 case
int n = in.nextInt();
int m = in.nextInt();
int[] dp = new int[1000000];
for (int i = 0; i <= m; i++) {
dp[i] = Integer.MAX_VALUE;
}
dp[n] = 0;
for (int i = n; i < m; i++) {
if (dp[i] == Integer.MAX_VALUE) {
//未曾到达的领域
continue;
}
//处理约数了
List list = getList(i);
for (int j : list) {
if (dp[i + j] != Integer.MAX_VALUE && i + j <= m) {
dp[i + j] = Math.min(dp[i + j], dp[i] + 1);
} else if (i + j <= m) {
dp[i + j] = dp[i] + 1;
}
}
}
if (dp[m] == Integer.MAX_VALUE) {
dp[m] = -1;
}
System.out.println(dp[m]);
}
}
private static List getList(int num) {
List list = new ArrayList<>();
for (int i = 2; i * i <= num; i++) {
if (num % i == 0) {
list.add(i);
if (num / i != i) {
list.add(num / i);
}
}
}
return list;
}
} 特殊情况当是1继续向下递归~~
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = scan.nextInt();
}
Arrays.sort(nums);
System.out.println(getSize(nums, n, 0, 0, 1));
}
private static int getSize(int[] nums, int n, int pos, int sum, int mul) {
int size = 0;
for (int i = pos; i < n; i++) {
sum += nums[i];
mul *= nums[i];
if (sum > mul) {
size = size + 1 + getSize(nums, n, i + 1, sum, mul);
} else if (nums[i] == 1) {
size = size + getSize(nums, n, i + 1, sum, mul);
} else {
break;
}
sum = sum - nums[i];
mul = mul / nums[i];
while (i < n - 1 && nums[i] == nums[i + 1]) {
i++;
}
}
return size;
}
}手套
public class Gloves {
public int findMinimum(int n, int[] left, int[] right) {
// write code here
int sum = 0;
int leftMin = 9999;
int leftSum = 0;
int rightMin = 99999;
int rightSum = 0;
for (int i = 0; i < n; i++) {
if (left[i] * right[i] == 0) {
sum += left[i] + right[i];
} else {
leftSum += left[i];
rightSum += right[i];
if (leftMin > left[i]) {
leftMin = left[i];
}
if (rightMin > right[i]) {
rightMin = right[i];
}
}
}
return sum + Math.min(leftSum - leftMin + 1, rightSum - rightMin + 1) + 1;
}
}扑克牌大小
先用一个symbol的String类型进行后续的比较,先看这俩个手牌有没有王炸 在那之后 如果是手牌的数量相等 比较最小牌即可、如果不同 这个时候 就是一个普通的手牌和一个炸弹手牌了,打印炸弹手牌即可,最后的情况就是手牌不相等的情况那就打印error即可~~
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
String str = scan.nextLine();
String[] pp = str.split("-");
String[] p1 = pp[0].split(" ");
String[] p2 = pp[1].split(" ");
String symbol = "34567891JQKA2";
if(pp[0].equals("joker JOKER") || pp[1].equals("joker JOKER") ){
System.out.println("joker JOKER");
}else if(p1.length == p2.length){
if(symbol.indexOf(pp[0].substring(0,1)) > symbol.indexOf(pp[1].substring(0,1))){
System.out.println(pp[0]);
}else{
System.out.println(pp[1]);
}
}else if(p1.length == 4){
System.out.println(pp[0]);
}else if(p2.length == 4){
System.out.println(pp[1]);
}else{
System.out.println("ERROR");
}
}
}查找两个字符串a,b中的最长公共子串
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (scan.hasNext()) { // 注意 while 处理多个 case
String str1 = scan.next();
String str2 = scan.next();
if(str1.length() <= str2.length()){
String result = getResult(str1, str2);
System.out.println(result);
}else{
String result = getResult(str2, str1);
System.out.println(result);
}
}
}
private static String getResult(String str1, String str2) {
int len1 = str1.length();
int len2 = str2.length();
int start = 0;
int maxLen = 0;
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1 ; i++) {
for (int j = 1; j <= len2; j++) {
if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
if(maxLen < dp[i][j]){
maxLen = dp[i][j];
start = i - maxLen;
}
}
}
}
return str1.substring(start,start+maxLen);
}
}年终奖
该题就是简单的动态规划,需要注意的是 在第一行第一列需要特殊处理一下。
星际密码
当n=1的时候 Xn = 1,当n = 2的时候,Xn = 2,当n = 3的时候 就是在矩阵![]() 再乘一个
再乘一个![]()
(1,1)那就是2*1 + 1* 1 = 3 那么此时的Xn = 3。这时候就能找到规律:f(n) = f(n-1) + f(n-2)~~
找到规律就好办了,这其实就是考察斐波那契数列。
public class Main {
public static void main(String[] args) {
int[] nums = new int[100001];
nums[1] = 1;
nums[2] = 2;
for(int i = 3;i <= 10000;i++){
nums[i] = nums[i-1] + nums[i-2];
nums[i] = nums[i] % 10000;
}
Scanner scan = new Scanner(System.in);
while(scan.hasNext()){
StringBuilder sb = new StringBuilder();
int n = scan.nextInt();
for(int i = 0;i < n;i++){
int xi = scan.nextInt();
sb.append(String.format("%04d",nums[xi]));
}
System.out.println(sb.toString());
}
}
}要特别注意的是 "%04d"的含义,是存4位不够4位的补0~~
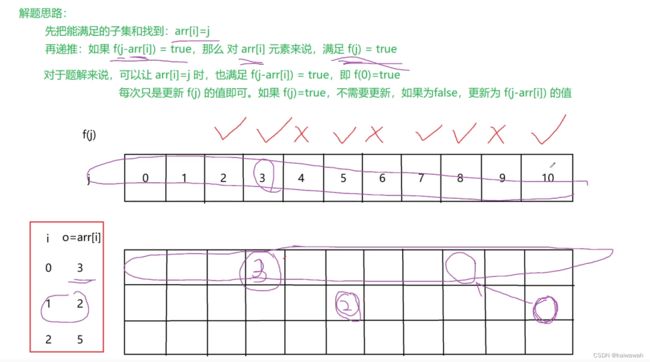
求正数数组的最小不可组成和
public int getFirstUnFormedNum(int[] arr) {
int max = 0;
int min = 9999999;
for(int i : arr){
min = Math.min(min,i);
max += i;
}
boolean[] result = new boolean[max+1];
result[0] = true;
for(int i : arr){
for(int j = max;j >= i;j--){
result[j] = result[j-i] || result[j];
}
}
for(int i = min;i < result.length;i++){
if(result[i] == false){
return i;
}
}
return max+1;
}