多线程编程-矩阵乘法
- 一、项目内容
- 1、利用Pthread 库编写程序实现多线程矩阵乘法
- 2、比较多线程与单线程计算的时间
- 二、项目环境
1、VMware Workstation Pro 虚拟机
2、Ubuntu 64位
3、Linux内核 4.7.3
4、GCC
5、内存2GB、处理器4
- 三、项目过程
实现n阶矩阵相乘,设计单线程、双线程和n*n线程算法,并计算各算法计算运行时间。
1、n阶操作矩阵随机产生,阶数由用户输入,用来测试程序运行时间。
核心代码:
| //生成随机数组、输出矩阵a,b srand((unsigned) time(NULL));//生成时间种子 for(i=0;i for(j=0;j { a[i][j]=rand()%11; b[i][j]=rand()%11; } |
2、双线程运算
将矩阵a拆分为两部分分别进入两个线程与b矩阵进行运算。
核心代码:
| //-----------------双线程操作函数------------------- void Thread1() { int i,j,m; for(i=0;(i for(j=0;j for(m=0;m { if(i%2==0) result[i][j]+=a[i][m]*b[m][j]; } } void Thread2() { int i,j,m; for(i=0;(i for(j=0;j for(m=0;m { if(i%2!=0) result[i][j]+=a[i][m]*b[m][j]; } } //----------------------双线程运算--------------------------- start3=clock(); pthread_create(&tid[0],NULL,(void*)Thread1,NULL); pthread_join(tid[0],NULL);//!!!!!!!!!!!! pthread_create(&tid[1],NULL,(void*)Thread2,NULL); pthread_join(tid[1],NULL); finish3=clock(); |
3、n*n多线程运算
产生n*n个线程,每组元素相乘a[i][j]*b[x][y]进入一个线程运算最后返回结果。
核心代码:
| //---------------多线程操作函数---------------------- void Thread(int *p) { int row=p[0]; int col=p[1]; int res=0; int l; for(l=0;l res+=a[row][l]*b[l][col]; result[row][col]=res; } start1=clock();//获得开始时间 for(i=0;i for(j=0;j { pass[i][j][0]=i; pass[i][j][1]=j; r=pthread_create(&thid[i][j],NULL,(void*)Thread,pass[i][j]); pthread_join(thid[i][j],NULL);//!!!!!!!!!!!! } finish1=clock();//获得结束时间 |
4、单线程运算
核心代码
| //---------------------单线程运算----------------------------- start2=clock(); for(i=0;i for(j=0;j for(m=0;m result[i][j]+=a[i][m]*b[m][j]; finish2=clock(); |
5、时间计算
使用函数clock()分别获取算法开始结束时间。
核心代码:
| start2=clock(); { 线程算法; } finish2=clock(); printf("------------------------------------------\n"); printf("矩阵阶数 :%d\n",n); printf("Single Thread calculate time is %g\n",(finish2-start2)); printf("n*n Mutli Thread calculate time is %g\n",(finish1-start1)); printf("2 Thread calculate time is %g\n",(finish3-start3)); |
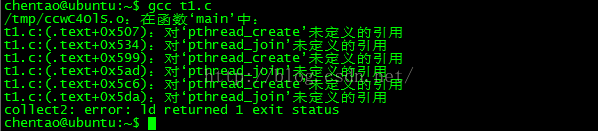
6、编译t1.c文件
编译时要链接pthread库
![]()
否则编译报错
- 四、项目源代码
#include
#include
#include
#include
//定义全局变量,防止越界将数组最大定为200
pthread_t thid[1000][1000];//n*n线程线程id
pthread_t tid[2];//双线程线程id
int pass[1000][1000][2];
int n;//矩阵阶数
int a[1000][1000],b[1000][1000];
int result[1000][1000];
int result1[1000][1000];
//-----------------双线程操作函数-------------------
void Thread1()
{
int i,j,m;
for(i=0;(i for(j=0;j for(m=0;m { if(i%2==0) result[i][j]+=a[i][m]*b[m][j]; } } void Thread2() { int i,j,m; for(i=0;(i for(j=0;j for(m=0;m { if(i%2!=0) result[i][j]+=a[i][m]*b[m][j]; } } //---------------多线程操作函数---------------------- void Thread(int *p) { int row=p[0]; int col=p[1]; int res=0; int l; for(l=0;l res+=a[row][l]*b[l][col]; result[row][col]=res; } //---------------------主函数------------------------ int main() { int i,j,m;//循环变量 double start1,finish1;//时间变量 double start2,finish2; double start3,finish3; int r; printf("请输入矩阵阶数(1~1000) n="); scanf("%d",&n); printf("----------------------------\n"); //生成随机数组、输出矩阵a,b srand((unsigned) time(NULL));//生成时间种子 for(i=0;i for(j=0;j { a[i][j]=rand()%11; b[i][j]=rand()%11; } printf("数组a:\n"); for(i=0;i { for(j=0;j { printf("%d ",a[i][j]); } printf("\n"); } printf("-----------------------------\n数组b:\n"); for(i=0;i { for(j=0;j { printf("%d ",b[i][j]); } printf("\n"); } //--------------------------n*n多线程运算------------------- start1=clock();//获得开始时间 for(i=0;i for(j=0;j { pass[i][j][0]=i; pass[i][j][1]=j; r=pthread_create(&thid[i][j],NULL,(void*)Thread,pass[i][j]); pthread_join(thid[i][j],NULL);//!!!!!!!!!!!! } finish1=clock();//获得结束时间 //----------------------双线程运算--------------------------- start3=clock(); pthread_create(&tid[0],NULL,(void*)Thread1,NULL); pthread_join(tid[0],NULL);//!!!!!!!!!!!! pthread_create(&tid[1],NULL,(void*)Thread2,NULL); pthread_join(tid[1],NULL);//!!!!!!!!!!!! finish3=clock(); //---------------------单线程运算----------------------------- start2=clock(); for(i=0;i for(j=0;j for(m=0;m result[i][j]+=a[i][m]*b[m][j]; finish2=clock(); //---------------------输出相乘计算结果----------------------- printf("计算结果:\n"); for(i=0;i { for(j=0;j { printf("%d ",result[i][j]); } printf("\n"); } printf("------------------------------------------\n"); printf("矩阵阶数 :%d\n",n); printf("Single Thread calculate time is %g\n",(finish2-start2)); printf("n*n Mutli Thread calculate time is %g\n",(finish1-start1)); printf("2 Thread calculate time is %g\n",(finish3-start3)); return 0; } 五、测试结果 测试1~200阶矩阵三个算法时间屏幕输出结果: 矩阵阶数: 1 | Single: 1 | Doube: 258 | n*n: 680 矩阵阶数: 2 | Single: 1 | Doube: 57 | n*n: 205 矩阵阶数: 3 | Single: 1 | Doube: 196 | n*n: 696 矩阵阶数: 4 | Single: 2 | Doube: 169 | n*n: 1729 矩阵阶数: 5 | Single: 3 | Doube: 168 | n*n: 7277 矩阵阶数: 6 | Single: 4 | Doube: 335 | n*n: 4406 矩阵阶数: 7 | Single: 11 | Doube: 536 | n*n: 8697 矩阵阶数: 8 | Single: 14 | Doube: 529 | n*n: 7808 矩阵阶数: 9 | Single: 10 | Doube: 150 | n*n: 8743 矩阵阶数: 10 | Single: 16 | Doube: 126 | n*n: 9062 矩阵阶数: 11 | Single: 17 | Doube: 150 | n*n: 14435 矩阵阶数: 12 | Single: 21 | Doube: 153 | n*n: 13634 矩阵阶数: 13 | Single: 29 | Doube: 198 | n*n: 17755 矩阵阶数: 14 | Single: 39 | Doube: 214 | n*n: 19840 矩阵阶数: 15 | Single: 41 | Doube: 150 | n*n: 19755 矩阵阶数: 16 | Single: 41 | Doube: 158 | n*n: 27677 矩阵阶数: 17 | Single: 64 | Doube: 129 | n*n: 24830 矩阵阶数: 18 | Single: 67 | Doube: 154 | n*n: 30602 矩阵阶数: 19 | Single: 80 | Doube: 150 | n*n: 35310 矩阵阶数: 20 | Single: 77 | Doube: 179 | n*n: 37081 矩阵阶数: 21 | Single: 137 | Doube: 263 | n*n: 42993 矩阵阶数: 22 | Single: 152 | Doube: 116 | n*n: 41800 矩阵阶数: 23 | Single: 116 | Doube: 184 | n*n: 46391 矩阵阶数: 24 | Single: 135 | Doube: 126 | n*n: 46630 矩阵阶数: 25 | Single: 183 | Doube: 97 | n*n: 52822 矩阵阶数: 26 | Single: 249 | Doube: 576 | n*n: 51433 矩阵阶数: 27 | Single: 252 | Doube: 150 | n*n: 68134 矩阵阶数: 28 | Single: 285 | Doube: 154 | n*n: 66447 矩阵阶数: 29 | Single: 281 | Doube: 155 | n*n: 67745 矩阵阶数: 30 | Single: 297 | Doube: 509 | n*n: 82265 矩阵阶数: 31 | Single: 356 | Doube: 155 | n*n: 81912 矩阵阶数: 32 | Single: 373 | Doube: 281 | n*n: 85291 矩阵阶数: 33 | Single: 444 | Doube: 151 | n*n: 93360 矩阵阶数: 34 | Single: 433 | Doube: 567 | n*n: 96435 矩阵阶数: 35 | Single: 491 | Doube: 217 | n*n: 106463 矩阵阶数: 36 | Single: 461 | Doube: 151 | n*n: 112124 矩阵阶数: 37 | Single: 587 | Doube: 159 | n*n: 110725 矩阵阶数: 38 | Single: 608 | Doube: 168 | n*n: 120463 矩阵阶数: 39 | Single: 738 | Doube: 148 | n*n: 121820 矩阵阶数: 40 | Single: 1130 | Doube: 584 | n*n: 133589 矩阵阶数: 41 | Single: 767 | Doube: 267 | n*n: 230811 矩阵阶数: 42 | Single: 839 | Doube: 152 | n*n: 153087 矩阵阶数: 43 | Single: 1301 | Doube: 890 | n*n: 152027 矩阵阶数: 44 | Single: 970 | Doube: 167 | n*n: 161993 矩阵阶数: 45 | Single: 886 | Doube: 130 | n*n: 171928 矩阵阶数: 46 | Single: 1002 | Doube: 1078 | n*n: 182704 矩阵阶数: 47 | Single: 1188 | Doube: 151 | n*n: 179778 矩阵阶数: 48 | Single: 1412 | Doube: 848 | n*n: 196881 矩阵阶数: 49 | Single: 1335 | Doube: 333 | n*n: 192894 矩阵阶数: 50 | Single: 1392 | Doube: 1077 | n*n: 206495 矩阵阶数: 51 | Single: 1541 | Doube: 165 | n*n: 237661 矩阵阶数: 52 | Single: 1557 | Doube: 1414 | n*n: 226139 矩阵阶数: 53 | Single: 1425 | Doube: 1383 | n*n: 232292 矩阵阶数: 54 | Single: 1599 | Doube: 1790 | n*n: 252953 矩阵阶数: 55 | Single: 1914 | Doube: 1690 | n*n: 291280 矩阵阶数: 56 | Single: 2387 | Doube: 1832 | n*n: 277845 矩阵阶数: 57 | Single: 2402 | Doube: 768 | n*n: 316884 矩阵阶数: 58 | Single: 2484 | Doube: 1971 | n*n: 310190 矩阵阶数: 59 | Single: 2583 | Doube: 1995 | n*n: 344781 矩阵阶数: 60 | Single: 2422 | Doube: 3791 | n*n: 346547 矩阵阶数: 61 | Single: 2755 | Doube: 4804 | n*n: 349948 矩阵阶数: 62 | Single: 2864 | Doube: 1476 | n*n: 343155 矩阵阶数: 63 | Single: 3448 | Doube: 1341 | n*n: 325463 矩阵阶数: 64 | Single: 3311 | Doube: 691 | n*n: 348237 矩阵阶数: 65 | Single: 4274 | Doube: 2789 | n*n: 418978 矩阵阶数: 66 | Single: 3457 | Doube: 4877 | n*n: 373926 矩阵阶数: 67 | Single: 4459 | Doube: 3172 | n*n: 448990 矩阵阶数: 68 | Single: 3355 | Doube: 1479 | n*n: 412369 矩阵阶数: 69 | Single: 4029 | Doube: 5101 | n*n: 397879 矩阵阶数: 70 | Single: 5476 | Doube: 3468 | n*n: 466528 矩阵阶数: 71 | Single: 5411 | Doube: 7749 | n*n: 469691 矩阵阶数: 72 | Single: 4286 | Doube: 3632 | n*n: 430718 矩阵阶数: 73 | Single: 5594 | Doube: 7353 | n*n: 462794 矩阵阶数: 74 | Single: 4914 | Doube: 991 | n*n: 452388 矩阵阶数: 75 | Single: 5472 | Doube: 7067 | n*n: 481377 矩阵阶数: 76 | Single: 5581 | Doube: 5857 | n*n: 478879 矩阵阶数: 77 | Single: 5678 | Doube: 9840 | n*n: 516341 矩阵阶数: 78 | Single: 5698 | Doube: 8898 | n*n: 534676 矩阵阶数: 79 | Single: 5922 | Doube: 7188 | n*n: 529238 矩阵阶数: 80 | Single: 7028 | Doube: 4830 | n*n: 536126 矩阵阶数: 81 | Single: 6735 | Doube: 8805 | n*n: 542658 矩阵阶数: 82 | Single: 6805 | Doube: 9232 | n*n: 576113 矩阵阶数: 83 | Single: 7206 | Doube: 9882 | n*n: 568683 矩阵阶数: 84 | Single: 8271 | Doube: 10469 | n*n: 594230 矩阵阶数: 85 | Single: 7672 | Doube: 7524 | n*n: 585913 矩阵阶数: 86 | Single: 10669 | Doube: 13695 | n*n: 671913 矩阵阶数: 87 | Single: 10866 | Doube: 17278 | n*n: 779806 矩阵阶数: 88 | Single: 24024 | Doube: 34293 | n*n: 995600 矩阵阶数: 89 | Single: 10190 | Doube: 17786 | n*n: 788592 矩阵阶数: 90 | Single: 9952 | Doube: 12725 | n*n: 749581 矩阵阶数: 91 | Single: 11038 | Doube: 10607 | n*n: 726252 矩阵阶数: 92 | Single: 10344 | Doube: 16335 | n*n: 783745 矩阵阶数: 93 | Single: 11647 | Doube: 18258 | n*n: 1.02869e+06 矩阵阶数: 94 | Single: 10289 | Doube: 16499 | n*n: 845672 矩阵阶数: 95 | Single: 13208 | Doube: 12921 | n*n: 972730 矩阵阶数: 96 | Single: 16351 | Doube: 49193 | n*n: 1.00211e+06 矩阵阶数: 97 | Single: 11378 | Doube: 17627 | n*n: 952054 矩阵阶数: 98 | Single: 18403 | Doube: 23564 | n*n: 1.35723e+06 矩阵阶数: 99 | Single: 16027 | Doube: 19736 | n*n: 1.07938e+06 矩阵阶数: 100 | Single: 15473 | Doube: 20589 | n*n: 1.09916e+06 矩阵阶数: 101 | Single: 17303 | Doube: 21052 | n*n: 1.06905e+06 矩阵阶数: 102 | Single: 17393 | Doube: 26692 | n*n: 1.13552e+06 矩阵阶数: 103 | Single: 17462 | Doube: 28304 | n*n: 1.63556e+06 矩阵阶数: 104 | Single: 19891 | Doube: 25893 | n*n: 1.24722e+06 矩阵阶数: 105 | Single: 22967 | Doube: 34187 | n*n: 1.21792e+06 矩阵阶数: 106 | Single: 19062 | Doube: 27997 | n*n: 1.23119e+06 矩阵阶数: 107 | Single: 24109 | Doube: 32898 | n*n: 1.24187e+06 矩阵阶数: 108 | Single: 24101 | Doube: 29358 | n*n: 1.39648e+06 矩阵阶数: 109 | Single: 30871 | Doube: 33334 | n*n: 1.44233e+06 矩阵阶数: 110 | Single: 28076 | Doube: 39116 | n*n: 1.56415e+06 矩阵阶数: 111 | Single: 24551 | Doube: 32546 | n*n: 1.35873e+06 矩阵阶数: 112 | Single: 21706 | Doube: 34472 | n*n: 1.46916e+06 矩阵阶数: 113 | Single: 25422 | Doube: 35378 | n*n: 1.38157e+06 矩阵阶数: 114 | Single: 24293 | Doube: 34713 | n*n: 1.41428e+06 矩阵阶数: 115 | Single: 26186 | Doube: 40845 | n*n: 1.43127e+06 矩阵阶数: 116 | Single: 26572 | Doube: 59439 | n*n: 1.64368e+06 矩阵阶数: 117 | Single: 40940 | Doube: 48102 | n*n: 1.68401e+06 矩阵阶数: 118 | Single: 27701 | Doube: 40660 | n*n: 1.64718e+06 矩阵阶数: 119 | Single: 27309 | Doube: 38076 | n*n: 1.6743e+06 矩阵阶数: 120 | Single: 28109 | Doube: 43205 | n*n: 1.56584e+06 矩阵阶数: 121 | Single: 31057 | Doube: 38103 | n*n: 1.58591e+06 矩阵阶数: 122 | Single: 28789 | Doube: 40813 | n*n: 1.5531e+06 矩阵阶数: 123 | Single: 31164 | Doube: 40672 | n*n: 1.54804e+06 矩阵阶数: 124 | Single: 29309 | Doube: 42329 | n*n: 1.58188e+06 矩阵阶数: 125 | Single: 32644 | Doube: 41968 | n*n: 1.66175e+06 矩阵阶数: 126 | Single: 31695 | Doube: 41374 | n*n: 1.6304e+06 矩阵阶数: 127 | Single: 33913 | Doube: 46943 | n*n: 1.67552e+06 矩阵阶数: 128 | Single: 37745 | Doube: 53524 | n*n: 1.88209e+06 矩阵阶数: 129 | Single: 35873 | Doube: 55831 | n*n: 2.06208e+06 矩阵阶数: 130 | Single: 37085 | Doube: 63925 | n*n: 2.0386e+06 矩阵阶数: 131 | Single: 34820 | Doube: 45524 | n*n: 1.81283e+06 矩阵阶数: 132 | Single: 35723 | Doube: 44034 | n*n: 1.68439e+06 矩阵阶数: 133 | Single: 35070 | Doube: 43090 | n*n: 1.69184e+06 矩阵阶数: 134 | Single: 39080 | Doube: 58516 | n*n: 1.71651e+06 矩阵阶数: 135 | Single: 37554 | Doube: 48365 | n*n: 1.79613e+06 矩阵阶数: 136 | Single: 36405 | Doube: 51691 | n*n: 1.72996e+06 矩阵阶数: 137 | Single: 35616 | Doube: 48402 | n*n: 1.80213e+06 矩阵阶数: 138 | Single: 39578 | Doube: 49691 | n*n: 1.81914e+06 矩阵阶数: 139 | Single: 36443 | Doube: 59963 | n*n: 1.80355e+06 矩阵阶数: 140 | Single: 39741 | Doube: 61044 | n*n: 1.81259e+06 矩阵阶数: 141 | Single: 44378 | Doube: 60496 | n*n: 1.8451e+06 矩阵阶数: 142 | Single: 39921 | Doube: 55631 | n*n: 1.85972e+06 矩阵阶数: 143 | Single: 41281 | Doube: 54693 | n*n: 1.92844e+06 矩阵阶数: 144 | Single: 42031 | Doube: 57105 | n*n: 1.90073e+06 矩阵阶数: 145 | Single: 46104 | Doube: 65977 | n*n: 1.96502e+06 矩阵阶数: 146 | Single: 42404 | Doube: 58334 | n*n: 1.95542e+06 矩阵阶数: 147 | Single: 39706 | Doube: 56344 | n*n: 1.98734e+06 矩阵阶数: 148 | Single: 49417 | Doube: 63989 | n*n: 1.98508e+06 矩阵阶数: 149 | Single: 51144 | Doube: 66638 | n*n: 2.03525e+06 矩阵阶数: 150 | Single: 44810 | Doube: 65124 | n*n: 2.05151e+06 矩阵阶数: 151 | Single: 50327 | Doube: 73334 | n*n: 2.19797e+06 矩阵阶数: 152 | Single: 58357 | Doube: 79002 | n*n: 2.16264e+06 矩阵阶数: 153 | Single: 51883 | Doube: 71693 | n*n: 2.19618e+06 矩阵阶数: 154 | Single: 76168 | Doube: 71583 | n*n: 2.16838e+06 矩阵阶数: 155 | Single: 54471 | Doube: 77879 | n*n: 2.25737e+06 矩阵阶数: 156 | Single: 58174 | Doube: 72524 | n*n: 2.28414e+06 矩阵阶数: 157 | Single: 59292 | Doube: 83070 | n*n: 2.35325e+06 矩阵阶数: 158 | Single: 56156 | Doube: 83911 | n*n: 2.42245e+06 矩阵阶数: 159 | Single: 55611 | Doube: 80793 | n*n: 2.39917e+06 矩阵阶数: 160 | Single: 63163 | Doube: 86986 | n*n: 2.38452e+06 矩阵阶数: 161 | Single: 60506 | Doube: 78943 | n*n: 2.39495e+06 矩阵阶数: 162 | Single: 60051 | Doube: 83139 | n*n: 2.43931e+06 矩阵阶数: 163 | Single: 75390 | Doube: 84982 | n*n: 2.47923e+06 矩阵阶数: 164 | Single: 62822 | Doube: 94593 | n*n: 2.51239e+06 矩阵阶数: 165 | Single: 60422 | Doube: 97632 | n*n: 2.49269e+06 矩阵阶数: 166 | Single: 68573 | Doube: 90956 | n*n: 2.58632e+06 矩阵阶数: 167 | Single: 61583 | Doube: 96046 | n*n: 2.56382e+06 矩阵阶数: 168 | Single: 67033 | Doube: 91160 | n*n: 2.59434e+06 矩阵阶数: 169 | Single: 69298 | Doube: 91149 | n*n: 2.62038e+06 矩阵阶数: 170 | Single: 65193 | Doube: 93222 | n*n: 2.63855e+06 矩阵阶数: 171 | Single: 68872 | Doube: 102268 | n*n: 2.67907e+06 矩阵阶数: 172 | Single: 68277 | Doube: 96865 | n*n: 2.7105e+06 矩阵阶数: 173 | Single: 72789 | Doube: 103044 | n*n: 2.73556e+06 矩阵阶数: 174 | Single: 76212 | Doube: 101176 | n*n: 2.75122e+06 矩阵阶数: 175 | Single: 77824 | Doube: 100159 | n*n: 2.81185e+06 矩阵阶数: 176 | Single: 77297 | Doube: 113760 | n*n: 2.84108e+06 矩阵阶数: 177 | Single: 81053 | Doube: 115173 | n*n: 2.85881e+06 矩阵阶数: 178 | Single: 75411 | Doube: 109014 | n*n: 2.89022e+06 矩阵阶数: 179 | Single: 78955 | Doube: 114459 | n*n: 2.92284e+06 矩阵阶数: 180 | Single: 83218 | Doube: 112747 | n*n: 2.98432e+06 矩阵阶数: 181 | Single: 84606 | Doube: 126328 | n*n: 3.14704e+06 矩阵阶数: 182 | Single: 92997 | Doube: 120457 | n*n: 3.17179e+06 矩阵阶数: 183 | Single: 87042 | Doube: 139498 | n*n: 3.13823e+06 矩阵阶数: 184 | Single: 94758 | Doube: 143461 | n*n: 3.21755e+06 矩阵阶数: 185 | Single: 107704 | Doube: 132428 | n*n: 3.34565e+06 矩阵阶数: 186 | Single: 96413 | Doube: 150912 | n*n: 3.34996e+06 矩阵阶数: 187 | Single: 91812 | Doube: 142600 | n*n: 3.38818e+06 矩阵阶数: 188 | Single: 97231 | Doube: 150768 | n*n: 3.42913e+06 矩阵阶数: 189 | Single: 99377 | Doube: 143366 | n*n: 3.46395e+06 矩阵阶数: 190 | Single: 104214 | Doube: 151076 | n*n: 3.51714e+06 矩阵阶数: 191 | Single: 107088 | Doube: 145833 | n*n: 3.49573e+06 矩阵阶数: 192 | Single: 119545 | Doube: 194584 | n*n: 3.60418e+06 矩阵阶数: 193 | Single: 115040 | Doube: 176783 | n*n: 3.97532e+06 矩阵阶数: 194 | Single: 120713 | Doube: 171265 | n*n: 4.00947e+06 矩阵阶数: 195 | Single: 127757 | Doube: 179445 | n*n: 4.20442e+06 矩阵阶数: 196 | Single: 124834 | Doube: 163651 | n*n: 4.02161e+06 矩阵阶数: 197 | Single: 128512 | Doube: 177221 | n*n: 4.16638e+06 矩阵阶数: 198 | Single: 143457 | Doube: 178970 | n*n: 4.17282e+06 矩阵阶数: 199 | Single: 121490 | Doube: 170773 | n*n: 3.88169e+06 矩阵阶数: 200 | Single: 131650 | Doube: 180263 | n*n: 4.00169e+06 图表分析: 根据数据图表分析,n*n线程进行乘法计算由于创建线程消耗大量时间导致并没有提高计算效率反而大幅度降低。对于单线程及双线程,在一定范围内,单线程计算所消耗时间仍然低于双线程,对于简单的计算,创建多线程反而是浪费时间,当矩阵阶数超过一定数值,计算复杂性上升,多线程优势更加明显。结果发现矩阵乘法计算效率要取决于计算负责度以及线程数量。 测试代码: #include #include #include #include //定义全局变量,防止越界将数组最大定为200 pthread_t thid[1000][1000];//n*n线程线程id pthread_t tid[2];//双线程线程id int pass[1000][1000][2]; int n;//矩阵阶数 int a[1000][1000],b[1000][1000]; int result[1000][1000]; int result1[1000][1000]; //-----------------双线程操作函数------------------- void Thread1() { int i,j,m; for(i=0;(i for(j=0;j for(m=0;m { if(i%2==0) result[i][j]+=a[i][m]*b[m][j]; } } void Thread2() { int i,j,m; for(i=0;(i for(j=0;j for(m=0;m { if(i%2!=0) result[i][j]+=a[i][m]*b[m][j]; } } //---------------多线程操作函数---------------------- void Thread(int *p) { int row=p[0]; int col=p[1]; int res=0; int l; for(l=0;l res+=a[row][l]*b[l][col]; result[row][col]=res; } //---------------------主函数------------------------ int main() { int t; for(t=1;t<200;t++) { int i,j,m;//循环变量 double start1,finish1;//时间变量 double start2,finish2; double start3,finish3; int r; n=t; //生成随机数组、输出矩阵a,b srand((unsigned) time(NULL));//生成时间种子 for(i=0;i for(j=0;j { a[i][j]=rand()%11; b[i][j]=rand()%11; } //--------------------------n*n多线程运算------------------- start1=clock();//获得开始时间 for(i=0;i for(j=0;j { pass[i][j][0]=i; pass[i][j][1]=j; r=pthread_create(&thid[i][j],NULL,(void*)Thread,pass[i][j]); pthread_join(thid[i][j],NULL);//!!!!!!!!!!!! } finish1=clock();//获得结束时间 //----------------------双线程运算--------------------------- start3=clock(); pthread_create(&tid[0],NULL,(void*)Thread1,NULL); pthread_join(tid[0],NULL);//!!!!!!!!!!!! pthread_create(&tid[1],NULL,(void*)Thread2,NULL); pthread_join(tid[1],NULL);//!!!!!!!!!!!! finish3=clock(); //---------------------单线程运算----------------------------- start2=clock(); for(i=0;i for(j=0;j for(m=0;m result[i][j]+=a[i][m]*b[m][j]; finish2=clock(); printf("矩阵阶数: %3d | Single: %10g | Doube: %10g | n*n: %10g\n",t,(finish2-start2),(finish3-start3),(finish1-start1)); } return 0; } 实现多线矩阵乘法过程中出现如下图问题: 算法并没与完成计算,通过测试输出创建线程返回值发现线程都是创建成功的。调试发现是未实现主线程的等待,导致子线程未执行结束即停止工作。 添加阻塞语句:pthread_join(tid[0],NULL); 修正后测试结果: