数据结构之双数组trie树

双数组Tire树定义：

双数组Trie（Double-ArrayTrie）是trie树的一个简单而有效的实现，由两个整数数组构成，一个是base[]，另一个是check[]。

base：数组中的每一个元素相当于Trie树的一个节点。

check：相当于当前状态的前一状态。

设数组下标为i,如果base[i],check[i]均为0,表示该位置为空。如果base[i]为负值，表示该状态为词语。Check[i]表示该状态的前一状态，t=base[i]+a,check[t]=i。

双数组Tire树基本构造过程：

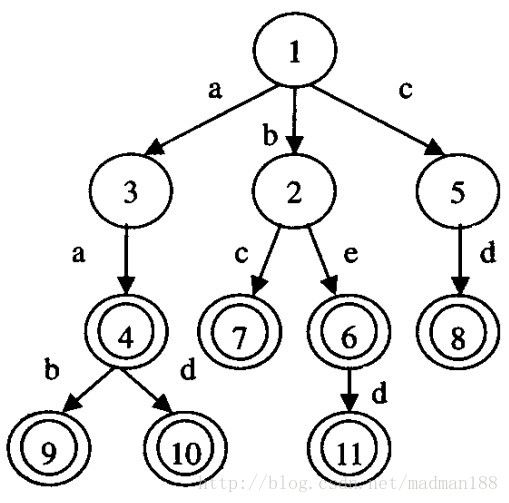
     数组初始化均为0，构造数组时结点访问顺序如结点序号。由于无论英文字母还是汉字在计算机中都由内码唯一表示，所以可用内码一一映射成序列码。假定各字母的序列码为a-1，b-2,c-3,d-4,e-5。因为词表中所有状态首字母“a,b,c”的序列码分别是1,2,3，所以必须把数组中这三个位置留给首字母。同时，因为叶子结点的表示是用该结点base数组下标乘以一1作为其在bas。数组中的值，而可结束状态表示是该结点bas。数组值乘以一1。为了使二者不产生混淆，所以每个具有可结束状态的非叶子结点其bas。数组值不能等于其数组下标。

     访问结点2:该结点状态b，序列码为2，对应数组下标为2。有两个分支结点，两个转移的变量序列码为3,5。所以base[2]取1即可，因为base[1+3]=check[1+3]=base[ 1+5]=check[1+5]=0。令base[2]=1,  check[4]=check[6」=2，结点6和7的数组下标为6和4.

     访问结点3:该结点状态为a，序列码为1，对应数组下标为1。只有一个状态转移的输人变量a，序列码为1  ,  base[1」可取4，因为base[4+1]=check[4+1〕=0。令base[1]=4，则结点4的数组下标为5,  check  [5]=1;

     访问结点4:该结点状态为na，已知其数组下标为5，由两个分支结点，两个转移的输人变量序列码分别为2,4o  base  [5]可取6，因为base[6+2]=check[6+2]=base[6+4]  =check[6+4]  =0。又因为该结点是一个可结束状态，所以令base[5]=(-1) *6，两个分支结点9和10的数组下标分别为|base[5] |  +2  =8和 | base[5] |+4=10  ,check[8]  =check  [10]=5;

     访问结点5:该结点状态为c，序列码为3，对应数组下标为3。有一个状态转移的输人变量d，序列码为4,base[3]可取3，因为base[3 +4] =check[3 +4] =0。令base[3]=3，子结点8的数组下标可知为7,check[7]  =3;

     访问结点6:该结点状态为be，已知对应数组下标为6，有一个状态转移的输人变量d列码为4,  base [6]可取5，因为base[5+4]=check[5+4=0。又因为该结点是一个可结束态，所以令base[6]=-5，其子结点11的数组下标为9,check[9]  =6;

     对于其他没有子结点的叶子结点，其bas。值用一1乘以相应的数组下标即可。

     最后可以得到:

     base[]={4,1,3，-4，-6，-5，-7，-8，-9，-10}

     check  []={0,0,0,2,1,2,3,5,6,5}

     数组构造完成后就可以进行查询了。如果要查字符串bec是否词表中的一个词，首先状态b的序列号2得到base[2]为1，接下来的输人变量是e,序列号为5  ,base[2]+5 = 6  ,check[6]为2，所以be是一个状态，可以继续。因为base[6]为-5，接下来的输人变量。序列号3, |base[6]|  +3  =8,check[8]为5，不是be的数组下标6，所以bec不是词表中的一个词。如果查的是bed,  d的序列号为4, |base[6]|+4  =9,check[9〕为6，同时base[9]等于-9，所以可判断bed是词表中的一个词。