布隆过滤器原理理解分享

问题：如何判断一个元素是否存在一个集合中？如果这个集合是海量的数据呢？例如数百亿垃圾邮件地址里面甄别某个邮件地址是否为垃圾邮件。

解决方法：布隆过滤器（Bloom Filter)

Bloom Filter 本质上是位向量（bit vector）与哈希结合的产物。至于哈希，学过数据结构的同学应该都记得的，没有学过的同学可以自行百度一下，其实现方式，提高性能的关键。这里简单描述一下其功能。

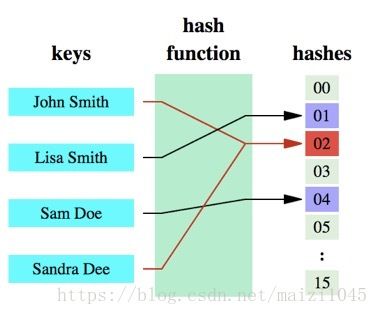
哈希函数的概念是：将原始数据转换成数据存放位置数据的函数，转换后的数据称为哈希值或哈希编码。下面是一幅示意图：

它的时间复杂度是O(1)，但是空间占用取决其优化的方式。它是布隆过滤器的基础。

布隆过滤器（Bloom Filter）的核心实现是一个超大的位数组（或者叫位向量）和几个哈希函数。假设位数组的长度为m，哈希函数的个数为k

以上图为例，具体的插入数据和校验是否存在的流程：

假设集合里面有3个元素{x, y, z}，哈希函数的个数为3。

Step1：将位数组初始化，每位都设置为0。

Step2：对于集合里面的每一个元素，将元素依次通过3个哈希函数进行映射，每次映射都会产生一个哈希值，哈希值对应位数组上面的一个点，将该位置标记为1。

Step3：查询W元素是否存在集合中的时候，同样的方法将W通过哈希映射到位数组上的3个点。

Step4：如果3个点的其中有一个点不为1，则可以判断该元素一定不存在集合中。反之，如果3个点都为1，则该元素可能存在集合中。注意：此处不能判断该元素是否一定存在集合中，可能存在一定的误判率。

可以从图中可以看到：假设某个元素通过映射对应下标为4，5，6这3个点。虽然这3个点都为1，但是很明显这3个点是不同元素经过哈希得到的位置，因此这种情况说明元素虽然不在集合中，也可能对应的都是1，这是误判率存在的原因。

以上是小白同学的理解，而实际使用时比这个复杂一些，下面是摘自谷歌黑板报里吴军写的一些分享。

在日常生活中，包括在设计计算机软件时，我们经常要判断一个元素是否在一个集合中。比如在字处理软件中，需要检查一个英语单词是否拼写正确（也就是要判断它是否在已知的字典中）；在 FBI，一个嫌疑人的名字是否已经在嫌疑名单上；在网络爬虫里，一个网址是否被访问过等等。最直接的方法就是将集合中全部的元素存在计算机中，遇到一个新元素时，将它和集合中的元素直接比较即可。一般来讲，计算机中的集合是用哈希表（hash table）来存储的。它的好处是快速准确，缺点是费存储空间。当集合比较小时，这个问题不显著，但是当集合巨大时，哈希表存储效率低的问题就显现出来了。比如说，一个象 Yahoo,Hotmail 和 Gmai 那样的公众电子邮件（email）提供商，总是需要过滤来自发送垃圾邮件的人（spamer）的垃圾邮件。一个办法就是记录下那些发垃圾邮件的 email 地址。由于那些发送者不停地在注册新的地址，全世界少说也有几十亿个发垃圾邮件的地址，将他们都存起来则需要大量的网络服务器。如果用哈希表，每存储一亿个 email 地址， 就需要 1.6GB 的内存（用哈希表实现的具体办法是将每一个 email 地址对应成一个八字节的信息指纹，然后将这些信息指纹存入哈希表，由于哈希表的存储效率一般只有 50%，因此一个 email 地址需要占用十六个字节。一亿个地址大约要 1.6GB， 即十六亿字节的内存）。因此存贮几十亿个邮件地址可能需要上百 GB 的内存。除非是超级计算机，一般服务器是无法存储的。
今天，我们介绍一种称作布隆过滤器的数学工具，它只需要哈希表 1/8 到 1/4 的大小就能解决同样的问题。
布隆过滤器是由巴顿.布隆于一九七零年提出的。它实际上是一个很长的二进制向量和一系列随机映射函数。我们通过上面的例子来说明起工作原理。
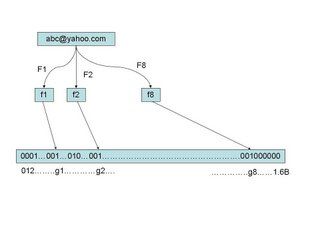
假定我们存储一亿个电子邮件地址，我们先建立一个十六亿二进制（比特），即两亿字节的向量，然后将这十六亿个二进制全部设置为零。对于每一个电子邮件地址 X，我们用八个不同的随机数产生器（F1,F2, ...,F8） 产生八个信息指纹（f1, f2, ..., f8）。再用一个随机数产生器 G 把这八个信息指纹映射到 1 到十六亿中的八个自然数 g1, g2, ...,g8。现在我们把这八个位置的二进制全部设置为一。当我们对这一亿个 email 地址都进行这样的处理后。一个针对这些 email 地址的布隆过滤器就建成了。（见下图）

现在，让我们看看如何用布隆过滤器来检测一个可疑的电子邮件地址 Y 是否在黑名单中。我们用相同的八个随机数产生器（F1, F2, ..., F8）对这个地址产生八个信息指纹 s1,s2,...,s8，然后将这八个指纹对应到布隆过滤器的八个二进制位，分别是 t1,t2,...,t8。如果 Y 在黑名单中，显然，t1,t2,..,t8 对应的八个二进制一定是1。这样在遇到任何在黑名单中的电子邮件地址，我们都能准确地发现。
布隆过滤器决不会漏掉任何一个在黑名单中的可疑地址。但是，它有一条不足之处。也就是它有极小的可能将一个不在黑名单中的电子邮件地址判定为在黑名单中，因为有可能某个好的邮件地址正巧对应个八个都被设置成1的二进制位。好在这种可能性很小。我们把它称为误识概率。在上面的例子中，误识概率在万分之一以下。
布隆过滤器的好处在于快速，省空间。但是有一定的误识别率。常见的补救办法是在建立一个小的白名单，存储那些可能别误判的邮件地址。