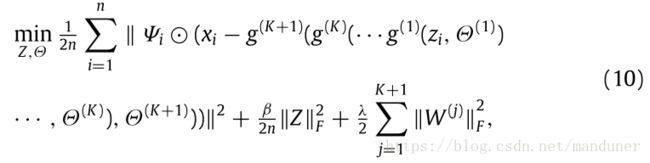论文阅读——矩阵填补模型之深度矩阵分解（Deep Matrix Factorization）

1，论文相关信息

Paper：Matrix completion by deep matrix factorization
Journal：Neural Networks
Year：2018

2，研究动机

（1）传统的矩阵填补模型（matrix completion）都是线性模型，不能应用于非线性的数据，而现实世界中，大部分数据都具有非线性结构。传统模型都是线性的原因，文中是这样解释的：
The low-rank assumption indicates that the data from linear latent variable models, in which the latent varibles are much fewer than the oberserved variables（注：针对文中这样的解释，我不太理解，为什么基于低秩的假设就表明数据是来自线性的隐变量模型，有哪位大神读过该篇论文的话，可以在评论区给出自己的见解，不胜感激）
（2）现有的非线性矩阵填补模型（matrix completion）对非线性的操作有限。例如，《Goal-Directed Inductive Matrix Completion》只将非线性操作应用到side information（辅助信息）上。
（3）现有的非线性矩阵填补模型的应用有限。例如，《Recognizing emotions from abstract paintings using non-linear matrix completion》中的模型只能应用于分类任务，而不能应用于矩阵填补常见的问题，例如，图像修复、协同过滤。

3，DMF模型构建

（1）传统矩阵填补模型，以矩阵分解（MF）为例，如下：

X=PZ X = P Z

模型中假设X是低秩的，这就意味着该模型是线性模型，所做的变换 X=PZ X = P Z 为线性变换
（2）以（1）为基础可构建具有非线性变换的矩阵填补模型， X=f(Z) X = f ( Z ) 。其中 f() f ( ) 表示非线性映射。这个思想也是构建本文DMF模型的核心思想
（3）以（1）（2）为前提可初步构建具有非线性结构的矩阵填补模型，如下：

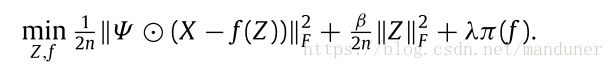
其中， λ,β λ , β 是正则项参数，也就是超参。 ⊙ ⊙ 表示Hadamard product（哈达马积，那么什么是哈达马积？这里简单说明一下，哈达马积表示两个同纬数的矩阵对应元素相乘，得到的还是和之前维数相同的矩阵）。 Ψ Ψ 为：

Ψ={1,0,if(i,j)∈Ωelse Ψ = { 1 , i f ( i , j ) ∈ Ω 0 , e l s e

（4）在（3）中没有具体说明非线性映射 f() f ( ) 到底是啥。然而确定（3）中非线性映射 f() f ( ) 的过程就是DMF模型的构建过程。
大家如果搞过神经网络，应该会知道神经网络拟合各种函数的强大能力。有这样的预备知识，咱们就可以顺理成章的用神经网络模型去拟合模型中的非线性映射了，那这就是本文的DMF模型了。
论文中，针对不同的应用，作者创建了具有不同隐藏层个数的DMF模型，分为单层神经网络模型和多层神经网络模型。

• 单层神经网络模型：

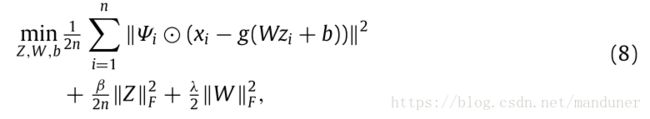
其中 g(.) g ( . ) 表示激活函数，常用的激活函数有sigmoid函数、tangent函数。激活函数的选择，是根据模型输出数据的范围确定的。

• 多层神经网络模型：
  
  其中，
  K K 表示隐藏层的层数

（5）通过单层模型或多层模型的训练可以得到非线性映射 g(.) g ( . ) 以及参数 W,b W , b 。这样就可以填补初始矩阵中的空白项了，计算公式如下：

4，DMF模型优化

采用了两种非线性的优化方法：BFGS、以及iRprop+。BFGS适用于测试数据矩阵较小的情况，iRprop+则适用于测试数据矩阵较大的情况。这两种优化方法不在这里阐述了，有兴趣的可以查看相应的资料，在参考资料中，我也给出了两种优化方法相对应的论文引用。

5，实验

（1）BaseLine方法

• MF：基本的矩阵分解模型
• NNM：最小化核函数
• TNNM：最小化截断核范数
• AECF：自编码器协同过滤模型
• LRFD：改进后的矩阵分解模型

（2）实验一：Matrix completion on a toy example of nonlinear data

（3）实验二：Single-image inpainting（单个RGB图像修复）

数据集为5张RGB图片：

（4）实验三：Group-image inpainting（一组图像修复）

数据集为MNIST dataset（手写字数据集）：

（5）实验四：Collabrative filtering（协同过滤）

数据集为如下两个：
- Jester-joke dataset-1
- MovieLens 100k

6，评价指标

归一化平均绝对误差NMAE（normalizedmeanabsolute error），公式如下：

7，参考资料

[1]Alameda-Pineda X, Ricci E, Yan Y, et al. Recognizing emotions from abstract paintings using non-linear matrix completion[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2016: 5240-5248.
[2]Fan J, Cheng J. Matrix completion by deep matrix factorization[J]. Neural Networks, 2018, 98: 34-41.
[3]Si S, Chiang K Y, Hsieh C J, et al. Goal-directed inductive matrix completion[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2016: 1165-1174.