Python 五子棋AI实现(3):极大极小值搜索和alpha beta剪枝
python 五子棋AI实现(3):极大极小值搜索和alpha beta剪枝
- 极大极小值搜索介绍
- alpha beta剪枝介绍
- MIN层剪枝
- MAX层剪枝
- 代码实现
- alpha,beta剪枝实现
- 获取子节点
- AI搜索深度和搜索时间
- 完整代码
- ChessAI.py
极大极小值搜索介绍
可以先回顾下上一篇中的AI 实现:AI 先获取当前所有可以下的位置(就是棋盘上的空格),然后每次在其中一个位置下子,根据棋型评估函数获取一个分数,所有位置都下过一遍后,从中获取评分最高的位置。这个就是极大值的搜索过程,我们称为 AI 的MAX层,即AI 要保证自己下棋的评分最大化。如果是轮到玩家下棋时,肯定会选取对自己最有利的位置,也可以说是对AI最不利的位置,即评分要最小化,我们称为AI的MIN层。。
上面是只有一层的搜索,如果要考虑多层搜索,第一层是AI下棋,第二层是玩家下棋,第三层是AI下棋,第四层是玩家下棋,依次类推。假设每一层有50个可选择的位置,每个位置看做树的一个节点,那么第一层是根节点下面的子节点,有50个节点,第二层是第一层下面的子节点,就有50×50个节点,第三层就有50×50×50个节点,依次类推,这样会形成一个巨大的博弈树。我们要做的就是搜索这棵树,找到对于AI最有利的下棋位置。
假设一个两层的博弈树,如图1所示,最上面一层是树的根节点,这里MAX表示会选取下一层子节点中评分最高的。第二层的MIN表示会选取下一层子节点中评分最低的。第三层是叶子节点,只需要计算评分。注意:只有在叶子节点时才会计算评分,在树的中间层,对于AI来说暂时是无法知道哪一个节点是最有利的。
图1 
极大极小值搜索是一个深度优先的算法,当第二层第一个节点的子节点都计算好评分后,因为这层是MIN层,会选取子节点中最低的评分作为这个节点的评分,就是3。依次类推,第二层第二个节点评分为6,第三个节点为5。当第二层节点都获取到评分后,因为第一层是MAX层,会选取子节点中最高的评分作为这个节点的评分,就是第二层第二个节点的评分6,这个节点所代表的下棋位置对于AI来说就是最有利的。最后算法返回评分6和第二层第二个节点的下棋位置。
根节点表示当前的棋局,博弈树上每一个节点就是从树根节点开始,每个子节点下一步棋,到该节点形成的新的棋局。 棋局就是所有已下棋位置的顺序列表,比如[ (7,7), (8,8), (7,9) ]。
图2 
比如图2的两层的博弈树,一开始玩家下了一步棋,位置是(7,7), 轮到AI下棋,AI进行博弈树搜索时,根节点已有的棋局就是 [ (7,7) ]。第二层时AI下棋,假设AI选择了三个下棋的位置(8,7),(8,8),(7,6),就形成了第二层的三个节点,这三个节点分别代表三个新的棋局,[ (7,7), (8,7) ], [ (7,7), (8,8) ], [ (7,7), (7,6) ]。 第三层轮到玩家下棋,看下中间评分为6的叶子节点,选择的下棋位置是(7,9), 所以这个叶节点的棋局是 [ (7,7), (8,8), (7,9 ],叶子节点的评分就是对这个棋局用棋型评估函数进行打分。
根据棋型评估函数 先确定下评分的定义:
假设AI 是黑棋,玩家是白棋,在某一层某个节点时的评分,就是对这个节点形成的棋局的评分:(AI 黑棋棋型的评分 - 玩家白棋棋形的评分):
极大极小值搜索算法就是在树的每一层搜索时,根据下面的策略:
- AI下棋的层,称为MAX层,这一层 AI 会选取子节点中评分最高的位置
- 玩家下棋的层,称为MIN层,这一层玩家会选取子节点中评分最低的位置
alpha beta剪枝介绍
极大极小值搜索算法的缺点就是当博弈树的层数变大时,需要搜索的节点数目会指数级增长。比如上面每一层的节点为50时,六层博弈树的节点就是50的6次方,运算时间会非常漫长。
在上面的例子中,我们会计算所有叶子节点的评分,但这个不是必要的。
Alpha-Beta剪枝就是用来将搜索树中不需要搜索的分支裁剪掉,以提高运算速度。基本的原理是:
- 当一个 MIN 层节点的 α值 ≤ β值时 ,剪掉该节点的所有未搜索子节点
- 当一个 MAX 层节点的 α值 ≥ β值时 ,剪掉该节点的所有未搜索子节点
其中α值是该层节点当前最有利的评分,β值是父节点当前的α值,根节点因为是MAX层,所以 β值 初始化为正无穷大(+∞)。
初始化节点的α值,如果是MAX层,初始化α值为负无穷大(-∞),这样子节点的评分肯定比这个值大。如果是MIN层,初始化α值为正无穷大(+∞),这样子节点的评分肯定比这个值小。
MIN层剪枝
我们先看一个MIN层剪枝的例子,根节点A的α, β值为(-∞, +∞),博弈树层数为2。
如图3,是开始搜索第二层第一个子节点B时的情况。因为节点B是在MIN层,所以α, β值设为(+∞, -∞),β值是父节点A当前的α值。
图3 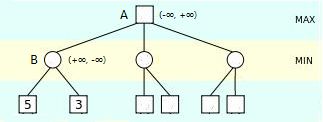
如图4,是搜索完节点B,并更新了节点B和根节点A的α值后,开始搜索第二层第二个节点C时的情况。根节点A的α值更新为当前最有利的评分3。节点C的α, β值设为(+∞, 3),β值是父节点A当前的α值。
图4 
如图5,是搜索完节点C,并更新了节点C和根节点A的α值后,开始搜索第二层第三个节点D时的情况。节点C的α值更新为6,根节点A的α值更新为当前最有利的评分6。节点D的α, β值设为(+∞, 6),β值是父节点A当前的α值。
图5 
如图6,就是MIN层剪枝的过程,搜索节点D的第一个子节点,得到的评分是5,更新节点D的α值为5,这时节点D 符合MIN层的剪枝判断: α值 ≤ β值,所以节点D的第二个子节点就被裁剪了。
图6 
MAX层剪枝
再看一个MAX层剪枝的例子,根节点A的α, β值为(-∞, +∞),博弈树层数为4。
如图7,是搜索完第三层第一个节点C的第一个子节点的情况。节点B是在MIN层,所以α, β值设为(+∞, -∞),节点C是在MAX层,所以α, β值设为(-∞,+∞)。节点C的第一个子节点初始α, β值设为(+∞, -∞),搜索完后α值更新为5。
图7 
如图8,是搜索完节点C后,更新完节点B的情况,节点C的α值更新为5, 节点B的α值同样更新为5。
图8 
如图9,是开始搜索节点B的第二个子节点D时的情况。节点D在MAX层,所以α, β值设为(-∞, 5), β值是父节点B当前的α值。
图9 
如图10,是搜索完节点D的第一个子节点后的情况。节点D的第一个子节点的评分为7,更新节点D的α值为7,这时节点D 符合MAX层的剪枝判断: α值 >= β值,所以节点D的第二个子节点就被裁剪了。
图10 
代码实现
alpha,beta剪枝实现
注意代码实现和上面的算法介绍有些不同: 子节点的β值是 父节点的 -α值,返回给父节点的评分是子节点的-α值。因为按照上面的剪枝算法,MIN层和MAX层的判断条件是不同的,为了代码实现的简洁,这样修改后就可以使用相同的选择最有利位置的条件:MAX层 和 MIN层 都选择最大的评分, 和相同的剪枝判断条件:MAX层 和 MIN层 都在 α值 ≥ β值时 ,剪掉该节点的所有未搜索子节点。
比如上面图1的例子,按照代码实现,就变成图11的样子。节点B的两个子节点的评分为5 和 3,返回到节点B时,就变成 -5 和 -3,这时选择最大的评分,就是 -3,对应的下棋位置和图1中还是一样的。节点B 和 节点D 按照同样的规则,选择最大的评分为 -6 和 -5。
节点A的三个子节点的评分分别为-3, -6 和 -5,返回到节点A时,评分就变成 3, 6 和 5,选择最大的评分,就是6,对应的节点C和图1还是一样的。
图11 
主要是修改了AI的search函数,新增的__search 函数实现了 AI的深度搜索和alpha,beta剪枝。
AI_SEARCH_DEPTH 表示搜索深度,默认是2,测试时可以改成4。
AI_SEARCH_DEPTH = 2
SCORE_MAX = 0x7fffffff
SCORE_MIN = -1 * SCORE_MAX
SCORE_FIVE = 10000
def __search(self, board, turn, depth, alpha = SCORE_MIN, beta = SCORE_MAX):
score = self.evaluate(board, turn)
if depth <= 0 or abs(score) >= SCORE_FIVE:
return score
moves = self.genmove(board, turn)
bestmove = None
self.alpha += len(moves)
# if there are no moves, just return the score
if len(moves) == 0:
return score
for _, x, y in moves:
board[y][x] = turn
if turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
op_turn = MAP_ENTRY_TYPE.MAP_PLAYER_TWO
else:
op_turn = MAP_ENTRY_TYPE.MAP_PLAYER_ONE
score = - self.__search(board, op_turn, depth - 1, -beta, -alpha)
board[y][x] = 0
self.belta += 1
# alpha/beta pruning
if score > alpha:
alpha = score
bestmove = (x, y)
if alpha >= beta:
break
if depth == self.maxdepth and bestmove:
self.bestmove = bestmove
return alpha
def search(self, board, turn, depth = 4):
self.maxdepth = depth
self.bestmove = None
score = self.__search(board, turn, depth)
x, y = self.bestmove
return score, x, y
获取子节点
上一篇文章中获取子节点的方法是,直接返回当前棋盘上所有空的位置。当搜索层数是1的时候,搜索节点最多225个,搜索时间可以忽略。但是当搜索层数变成2,4时,需要搜索的节点就变成 255×255,或255×255×255×255,这个搜索时间就太长了。
注意到很多空的位置是没有价值的,比如不能和已有的棋子形成棋型,或者挡住对方的棋型,可以直接忽略这些位置。
所以只考虑在已下双方棋子的一定范围内的空位置,可以考虑在范围1内的棋子。
比如下面只下了2步棋的棋盘上,范围1内的空位置有12个。

修改后的genmove函数,获取已下双方棋子范围1内的空位置。hasNeighbor函数,判断空位置范围1内是否有已下的棋子。
def hasNeighbor(self, board, x, y, radius):
start_x, end_x = (x - radius), (x + radius)
start_y, end_y = (y - radius), (y + radius)
for i in range(start_y, end_y+1):
for j in range(start_x, end_x+1):
if i >= 0 and i < self.len and j >= 0 and j < self.len:
if board[i][j] != 0:
return True
return False
# get all positions near chess
def genmove(self, board, turn):
fives = []
mfours, ofours = [], []
msfours, osfours = [], []
if turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
mine = 1
opponent = 2
else:
mine = 2
opponent = 1
moves = []
radius = 1
for y in range(self.len):
for x in range(self.len):
if board[y][x] == 0 and self.hasNeighbor(board, x, y, radius):
score = self.pos_score[y][x]
moves.append((score, x, y))
moves.sort(reverse=True)
return moves
AI搜索深度和搜索时间
搜索深度就是博弈树的层数,博弈树的层数越多,AI就越厉害。但是由于搜索时间会指数级增加,所以这里只测试了深度为2和4的情况。
- 搜索深度为2,搜索时间基本在1秒以内。下面时程序运行时的统计信息,这边的alpha值可以看成是不开启剪枝会搜索的节点数目,(alpha - beta)值可以看成是裁剪掉的节点数目。
time[0.04] (8, 8), score[-6] alpha[96] belta[28]
time[0.04] (8, 7), score[-10] alpha[271] belta[43]
time[0.09] (7, 8), score[-398] alpha[304] belta[115]
time[0.07] (9, 5), score[-402] alpha[378] belta[125]
time[0.29] (4, 10), score[-392] alpha[693] belta[566]
time[0.15] (9, 6), score[-16] alpha[1041] belta[232]
time[0.16] (10, 5), score[-20] alpha[980] belta[245]
time[0.23] (7, 5), score[-22] alpha[1388] belta[321] - 搜索深度为4, 搜索时间不稳定,可能会到20秒。后续会优化到搜索时间在2秒左右。
time[0.73] (8, 8), score[-10] alpha[5275] belta[1388]
time[1.63] (6, 8), score[-394] alpha[11835] belta[3122]
time[1.19] (8, 7), score[-398] alpha[10195] belta[1859]
time[1.49] (7, 6), score[-400] alpha[12053] belta[2382]
time[4.27] (6, 5), score[-402] alpha[25392] belta[7005]
time[3.65] (6, 7), score[-394] alpha[35265] belta[5135]
time[5.82] (8, 5), score[-8] alpha[36939] belta[8458]
完整代码
一共有三个文件,main.py, GameMap.py 和 ChessAI.py。这次只修改了ChessAI.py,前两个文件可以看上两篇文章中的代码。
ChessAI.py
from GameMap import *
from enum import IntEnum
from random import randint
import time
AI_SEARCH_DEPTH = 2
class CHESS_TYPE(IntEnum):
NONE = 0,
SLEEP_TWO = 1,
LIVE_TWO = 2,
SLEEP_THREE = 3
LIVE_THREE = 4,
CHONG_FOUR = 5,
LIVE_FOUR = 6,
LIVE_FIVE = 7,
CHESS_TYPE_NUM = 8
FIVE = CHESS_TYPE.LIVE_FIVE.value
FOUR, THREE, TWO = CHESS_TYPE.LIVE_FOUR.value, CHESS_TYPE.LIVE_THREE.value, CHESS_TYPE.LIVE_TWO.value
SFOUR, STHREE, STWO = CHESS_TYPE.CHONG_FOUR.value, CHESS_TYPE.SLEEP_THREE.value, CHESS_TYPE.SLEEP_TWO.value
SCORE_MAX = 0x7fffffff
SCORE_MIN = -1 * SCORE_MAX
SCORE_FIVE = 10000
class ChessAI():
def __init__(self, chess_len):
self.len = chess_len
# [horizon, vertical, left diagonal, right diagonal]
self.record = [[[0,0,0,0] for x in range(chess_len)] for y in range(chess_len)]
self.count = [[0 for x in range(CHESS_TYPE_NUM)] for i in range(2)]
self.pos_score = [[(7 - max(abs(x - 7), abs(y - 7))) for x in range(chess_len)] for y in range(chess_len)]
def reset(self):
for y in range(self.len):
for x in range(self.len):
for i in range(4):
self.record[y][x][i] = 0
for i in range(len(self.count)):
for j in range(len(self.count[0])):
self.count[i][j] = 0
def click(self, map, x, y, turn):
map.click(x, y, turn)
def isWin(self, board, turn):
return self.evaluate(board, turn, True)
# check if has a none empty position in it's radius range
def hasNeighbor(self, board, x, y, radius):
start_x, end_x = (x - radius), (x + radius)
start_y, end_y = (y - radius), (y + radius)
for i in range(start_y, end_y+1):
for j in range(start_x, end_x+1):
if i >= 0 and i < self.len and j >= 0 and j < self.len:
if board[i][j] != 0:
return True
return False
# get all positions near chess
def genmove(self, board, turn):
fives = []
mfours, ofours = [], []
msfours, osfours = [], []
if turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
mine = 1
opponent = 2
else:
mine = 2
opponent = 1
moves = []
radius = 1
for y in range(self.len):
for x in range(self.len):
if board[y][x] == 0 and self.hasNeighbor(board, x, y, radius):
score = self.pos_score[y][x]
moves.append((score, x, y))
moves.sort(reverse=True)
return moves
def __search(self, board, turn, depth, alpha = SCORE_MIN, beta = SCORE_MAX):
score = self.evaluate(board, turn)
if depth <= 0 or abs(score) >= SCORE_FIVE:
return score
moves = self.genmove(board, turn)
bestmove = None
self.alpha += len(moves)
# if there are no moves, just return the score
if len(moves) == 0:
return score
for _, x, y in moves:
board[y][x] = turn
if turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
op_turn = MAP_ENTRY_TYPE.MAP_PLAYER_TWO
else:
op_turn = MAP_ENTRY_TYPE.MAP_PLAYER_ONE
score = - self.__search(board, op_turn, depth - 1, -beta, -alpha)
board[y][x] = 0
self.belta += 1
# alpha/beta pruning
if score > alpha:
alpha = score
bestmove = (x, y)
if alpha >= beta:
break
if depth == self.maxdepth and bestmove:
self.bestmove = bestmove
return alpha
def search(self, board, turn, depth = 4):
self.maxdepth = depth
self.bestmove = None
score = self.__search(board, turn, depth)
x, y = self.bestmove
return score, x, y
def findBestChess(self, board, turn):
time1 = time.time()
self.alpha = 0
self.belta = 0
score, x, y = self.search(board, turn, AI_SEARCH_DEPTH)
time2 = time.time()
print('time[%.2f] (%d, %d), score[%d] alpha[%d] belta[%d]' % ((time2-time1), x, y, score, self.alpha, self.belta))
return (x, y)
# calculate score, FIXME: May Be Improved
def getScore(self, mine_count, opponent_count):
mscore, oscore = 0, 0
if mine_count[FIVE] > 0:
return (SCORE_FIVE, 0)
if opponent_count[FIVE] > 0:
return (0, SCORE_FIVE)
if mine_count[SFOUR] >= 2:
mine_count[FOUR] += 1
if opponent_count[SFOUR] >= 2:
opponent_count[FOUR] += 1
if mine_count[FOUR] > 0:
return (9050, 0)
if mine_count[SFOUR] > 0:
return (9040, 0)
if opponent_count[FOUR] > 0:
return (0, 9030)
if opponent_count[SFOUR] > 0 and opponent_count[THREE] > 0:
return (0, 9020)
if mine_count[THREE] > 0 and opponent_count[SFOUR] == 0:
return (9010, 0)
if (opponent_count[THREE] > 1 and mine_count[THREE] == 0 and mine_count[STHREE] == 0):
return (0, 9000)
if opponent_count[SFOUR] > 0:
oscore += 400
if mine_count[THREE] > 1:
mscore += 500
elif mine_count[THREE] > 0:
mscore += 100
if opponent_count[THREE] > 1:
oscore += 2000
elif opponent_count[THREE] > 0:
oscore += 400
if mine_count[STHREE] > 0:
mscore += mine_count[STHREE] * 10
if opponent_count[STHREE] > 0:
oscore += opponent_count[STHREE] * 10
if mine_count[TWO] > 0:
mscore += mine_count[TWO] * 6
if opponent_count[TWO] > 0:
oscore += opponent_count[TWO] * 6
if mine_count[STWO] > 0:
mscore += mine_count[STWO] * 2
if opponent_count[STWO] > 0:
oscore += opponent_count[STWO] * 2
return (mscore, oscore)
def evaluate(self, board, turn, checkWin=False):
self.reset()
if turn == MAP_ENTRY_TYPE.MAP_PLAYER_ONE:
mine = 1
opponent = 2
else:
mine = 2
opponent = 1
for y in range(self.len):
for x in range(self.len):
if board[y][x] == mine:
self.evaluatePoint(board, x, y, mine, opponent)
elif board[y][x] == opponent:
self.evaluatePoint(board, x, y, opponent, mine)
mine_count = self.count[mine-1]
opponent_count = self.count[opponent-1]
if checkWin:
return mine_count[FIVE] > 0
else:
mscore, oscore = self.getScore(mine_count, opponent_count)
return (mscore - oscore)
def evaluatePoint(self, board, x, y, mine, opponent, count=None):
dir_offset = [(1, 0), (0, 1), (1, 1), (1, -1)] # direction from left to right
ignore_record = True
if count is None:
count = self.count[mine-1]
ignore_record = False
for i in range(4):
if self.record[y][x][i] == 0 or ignore_record:
self.analysisLine(board, x, y, i, dir_offset[i], mine, opponent, count)
# line is fixed len 9: XXXXMXXXX
def getLine(self, board, x, y, dir_offset, mine, opponent):
line = [0 for i in range(9)]
tmp_x = x + (-5 * dir_offset[0])
tmp_y = y + (-5 * dir_offset[1])
for i in range(9):
tmp_x += dir_offset[0]
tmp_y += dir_offset[1]
if (tmp_x < 0 or tmp_x >= self.len or
tmp_y < 0 or tmp_y >= self.len):
line[i] = opponent # set out of range as opponent chess
else:
line[i] = board[tmp_y][tmp_x]
return line
def analysisLine(self, board, x, y, dir_index, dir, mine, opponent, count):
# record line range[left, right] as analysized
def setRecord(self, x, y, left, right, dir_index, dir_offset):
tmp_x = x + (-5 + left) * dir_offset[0]
tmp_y = y + (-5 + left) * dir_offset[1]
for i in range(left, right+1):
tmp_x += dir_offset[0]
tmp_y += dir_offset[1]
self.record[tmp_y][tmp_x][dir_index] = 1
empty = MAP_ENTRY_TYPE.MAP_EMPTY.value
left_idx, right_idx = 4, 4
line = self.getLine(board, x, y, dir, mine, opponent)
while right_idx < 8:
if line[right_idx+1] != mine:
break
right_idx += 1
while left_idx > 0:
if line[left_idx-1] != mine:
break
left_idx -= 1
left_range, right_range = left_idx, right_idx
while right_range < 8:
if line[right_range+1] == opponent:
break
right_range += 1
while left_range > 0:
if line[left_range-1] == opponent:
break
left_range -= 1
chess_range = right_range - left_range + 1
if chess_range < 5:
setRecord(self, x, y, left_range, right_range, dir_index, dir)
return CHESS_TYPE.NONE
setRecord(self, x, y, left_idx, right_idx, dir_index, dir)
m_range = right_idx - left_idx + 1
# M:mine chess, P:opponent chess or out of range, X: empty
if m_range >= 5:
count[FIVE] += 1
# Live Four : XMMMMX
# Chong Four : XMMMMP, PMMMMX
if m_range == 4:
left_empty = right_empty = False
if line[left_idx-1] == empty:
left_empty = True
if line[right_idx+1] == empty:
right_empty = True
if left_empty and right_empty:
count[FOUR] += 1
elif left_empty or right_empty:
count[SFOUR] += 1
# Chong Four : MXMMM, MMMXM, the two types can both exist
# Live Three : XMMMXX, XXMMMX
# Sleep Three : PMMMX, XMMMP, PXMMMXP
if m_range == 3:
left_empty = right_empty = False
left_four = right_four = False
if line[left_idx-1] == empty:
if line[left_idx-2] == mine: # MXMMM
setRecord(self, x, y, left_idx-2, left_idx-1, dir_index, dir)
count[SFOUR] += 1
left_four = True
left_empty = True
if line[right_idx+1] == empty:
if line[right_idx+2] == mine: # MMMXM
setRecord(self, x, y, right_idx+1, right_idx+2, dir_index, dir)
count[SFOUR] += 1
right_four = True
right_empty = True
if left_four or right_four:
pass
elif left_empty and right_empty:
if chess_range > 5: # XMMMXX, XXMMMX
count[THREE] += 1
else: # PXMMMXP
count[STHREE] += 1
elif left_empty or right_empty: # PMMMX, XMMMP
count[STHREE] += 1
# Chong Four: MMXMM, only check right direction
# Live Three: XMXMMX, XMMXMX the two types can both exist
# Sleep Three: PMXMMX, XMXMMP, PMMXMX, XMMXMP
# Live Two: XMMX
# Sleep Two: PMMX, XMMP
if m_range == 2:
left_empty = right_empty = False
left_three = right_three = False
if line[left_idx-1] == empty:
if line[left_idx-2] == mine:
setRecord(self, x, y, left_idx-2, left_idx-1, dir_index, dir)
if line[left_idx-3] == empty:
if line[right_idx+1] == empty: # XMXMMX
count[THREE] += 1
else: # XMXMMP
count[STHREE] += 1
left_three = True
elif line[left_idx-3] == opponent: # PMXMMX
if line[right_idx+1] == empty:
count[STHREE] += 1
left_three = True
left_empty = True
if line[right_idx+1] == empty:
if line[right_idx+2] == mine:
if line[right_idx+3] == mine: # MMXMM
setRecord(self, x, y, right_idx+1, right_idx+2, dir_index, dir)
count[SFOUR] += 1
right_three = True
elif line[right_idx+3] == empty:
#setRecord(self, x, y, right_idx+1, right_idx+2, dir_index, dir)
if left_empty: # XMMXMX
count[THREE] += 1
else: # PMMXMX
count[STHREE] += 1
right_three = True
elif left_empty: # XMMXMP
count[STHREE] += 1
right_three = True
right_empty = True
if left_three or right_three:
pass
elif left_empty and right_empty: # XMMX
count[TWO] += 1
elif left_empty or right_empty: # PMMX, XMMP
count[STWO] += 1
# Live Two: XMXMX, XMXXMX only check right direction
# Sleep Two: PMXMX, XMXMP
if m_range == 1:
left_empty = right_empty = False
if line[left_idx-1] == empty:
if line[left_idx-2] == mine:
if line[left_idx-3] == empty:
if line[right_idx+1] == opponent: # XMXMP
count[STWO] += 1
left_empty = True
if line[right_idx+1] == empty:
if line[right_idx+2] == mine:
if line[right_idx+3] == empty:
if left_empty: # XMXMX
#setRecord(self, x, y, left_idx, right_idx+2, dir_index, dir)
count[TWO] += 1
else: # PMXMX
count[STWO] += 1
elif line[right_idx+2] == empty:
if line[right_idx+3] == mine and line[right_idx+4] == empty: # XMXXMX
count[TWO] += 1
return CHESS_TYPE.NONE