原文首发于 baishusama.github.io,欢迎围观~
肝不动业务代码的时候,就时不时地做个题吧/w\
题目要求
原题目:461. Hamming Distance
维基百科中的“汉明距离”:
在信息论中,两个等长字符串之间的汉明距离(英语:Hamming distance)是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。
题干:现在求两个整数 x 和 y 之间的汉明距离,其中,0 ≤ x, y < 2^31。
思路
根据汉明距离的定义、再结合原题目中的“Explanation”部分,可以得知我们需要对整数 x,y 对应的二进制数逐位累加差异——统计得到的不相同的位的个数,即为所求。
- 思路一
- 我们要么先将整数转换成二进制——但是由于 JavaScript 只有一个 Number 类型用来表示数字,所以二进制数只能用别的方式代为表示——e.g.
4的二进制数可以表示为字符串(4).toString(2); // "100",或者数组[1,0,0](数组好像没有直接的转换方法?)。 - 再对字符串或者数组中的“二进制值”做求解/求和。
- 我们要么先将整数转换成二进制——但是由于 JavaScript 只有一个 Number 类型用来表示数字,所以二进制数只能用别的方式代为表示——e.g.
- 思路二
- 虽然 JavaScript 不能很好地支持二进制数的表示,但是 JS 中天然有位操作符——其中,异或
^恰好能满足我们的需求!- 如果
x异或y得到z(z = x ^ y),那么z对应的二进制表示中 1 的个数即为所求。
- 如果
- 故再逐位求和即可:
- 首先我们来看看,一个变量和 1 做与操作(
&)会有什么现象:-
val & 1,如果val的最右一位是 1 那么结果是 1 ; -
val & 1,如果val的最右一位是 0 那么结果是 0 。
-
- 此时我们至少能判断最右一位的 01 情况了。
- 那么再结合右移位操作
>>来不断使高位逐个变成最右位,我们就能计算一个二进制数的所有位的 01 情况!
- 首先我们来看看,一个变量和 1 做与操作(
- 虽然 JavaScript 不能很好地支持二进制数的表示,但是 JS 中天然有位操作符——其中,异或
其实按照上述思路来看,整体是分成两个步骤的:
- 得到差异
- 累加差异
两个步骤均可以用一下两种方式二选一解决:
- 位操作
- 其他数据结构,比如字符串
所以可以 2 * 2 = 4 组合出四种大致思路。而第一步的“得到差异”个人比较推荐的做法是用异或一步到位。(后续实现中的第一步均采取了异或。)
更多的 JS 相关的位操作符请参考 Bitwise operators @MDN。
代码实现
实现一
先异或再转字符串最后通过 match 方法(正则)计数的实现:
/**
* @param {number} x
* @param {number} y
* @return {number}
*/
var hammingDistance = function(x, y) {
var xor = x ^ y;
var str = xor.toString(2);
var match = str.match(/1/g); // 用正则匹配计算个数;match 为 null 或者数组。
return match ? match.length : 0 ;
};
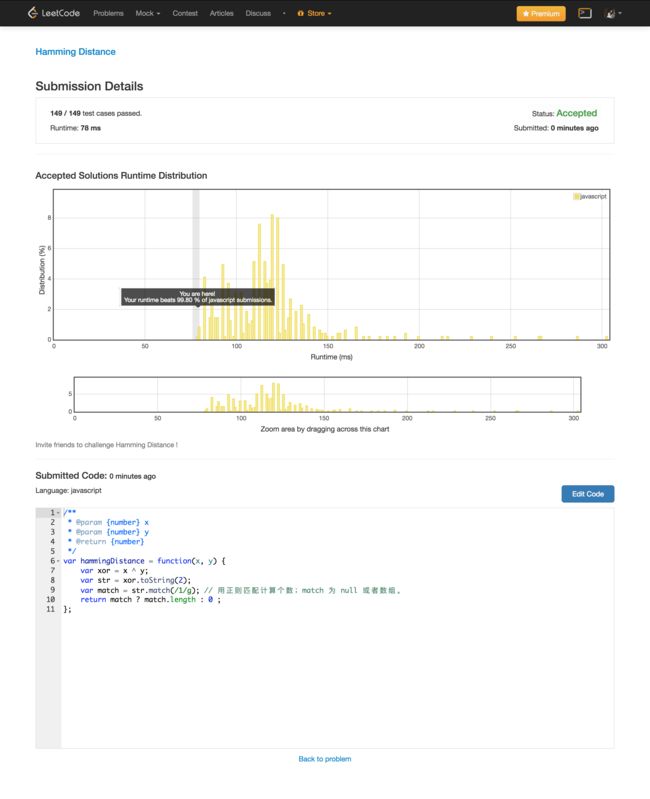
提交详情:
实现二
先异或再转字符串最后通过 split 方法计数的实现:
/**
* @param {number} x
* @param {number} y
* @return {number}
*/
var hammingDistance = function(x, y) {
var xor = x ^ y;
var str = xor.toString(2);
return str.split('1').length - 1; // 通过 split 计算某个字符(串)出现的个数
};
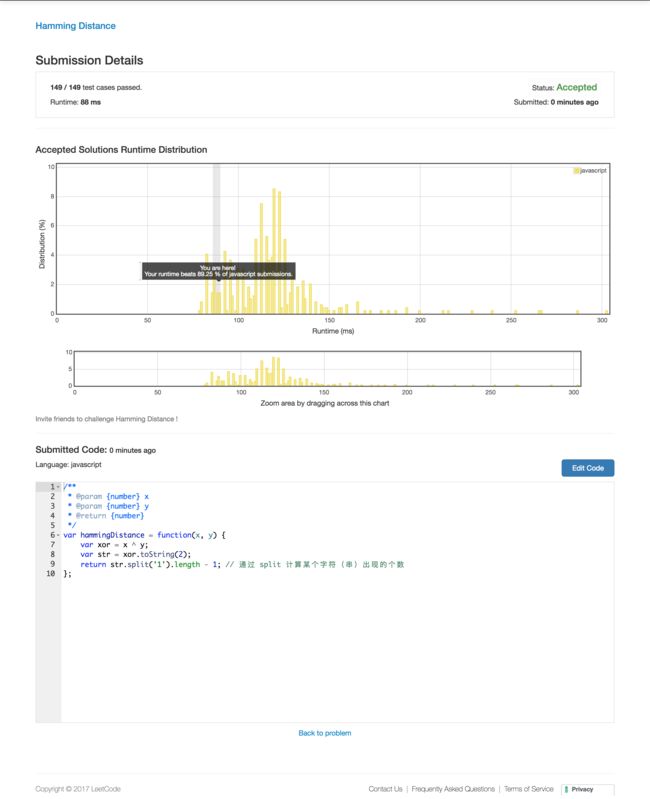
提交详情:
实现三
完全的位操作实现:
/**
* @param {number} x
* @param {number} y
* @return {number}
*/
var hammingDistance = function(x, y) {
var xor = x ^ y;
var sum = 0;
sum += xor & 1;
while(xor = xor >> 1){
sum += xor & 1;
}
return sum;
};
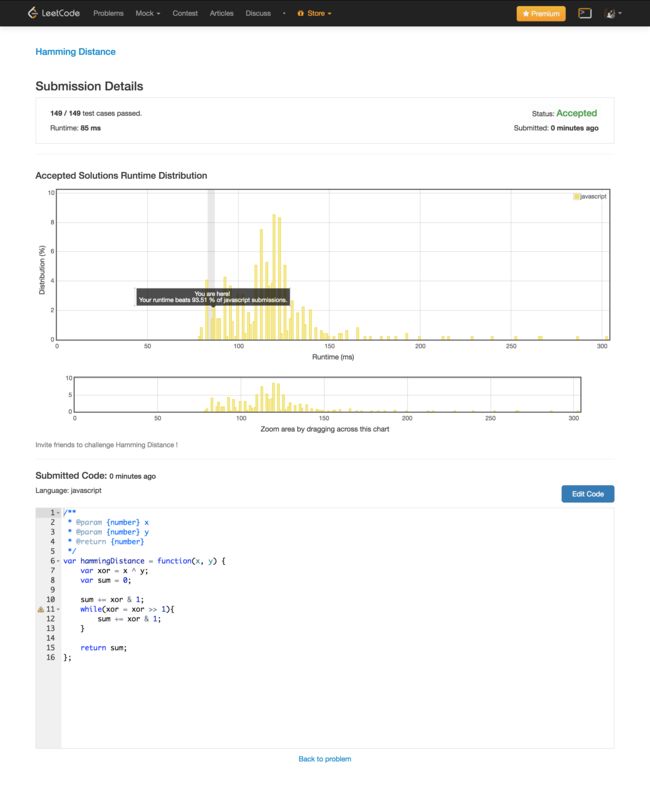
提交详情:
结果分析
其实第一个提交详情的图里的 runtime 和 distribution 不太可信,因为我第一次截实现一的详情图的时候,结果是“Your runtime beats 94.43 % of javascript submissions.”,后来我重新 submit 再打开之后,就变成“99.80 %”了……然后为了满足自己的虚荣心,贴了第二次的图(不要打我)。
其他解法
/**
* @param {number} x
* @param {number} y
* @return {number}
*/
var hammingDistance = function(x, y) {
let n = x ^ y;
let count = 0;
while (n) {
n = n & (n - 1)
count++;
}
return count;
};
第一眼看到这个排名极靠前、完全位操作实现的解法的时候,虽然看不懂,但是可以看出这个 accepted 的解法中的 while 在最少的循环次内就得到了结果。
因为在我的完全位操作的实现(实现三)中,当最高位是 1 的那一位在越高位的时候,while 就会循环越多次,如果最高位的 1 在第 M 位(M >= 0),那么循环条件将执行 M+1 次,循环体将执行 M 次,即很多是 0 的位也被列入总和—— 0 虽然并不会对总和产生影响,但是多执行的代码会增加时间上的开销。
而上面这个解法中能够只执行 count 次就结束循环,堪称完美!那么,现在我们来看看最为关键的代码 n = n & (n - 1) 有什么奥秘。
二进制数减一是一个奇妙的操作——当一个二进制数减一的时候,低位的 0 会变成 1,直到遇到一个最低位的 1 被减成 0。假设这个数 n 中最低位的 1 位于第 m 位(m >= 0),最高位的 1 位于第 M 位,最高位为第 N 位。那么此时,0~m 位各位上的数字都做了取反操作(包含一个 m 位的 1 和 0 ~ m-1 位的所有 0),而 m+1 ~ N 位各位上的数字都保持不变,即数 n 与上 (n - 1) 会导致 0~m 位均变成 0 ,这个过程中影响到了最低位(m 位上的一个 1)。即,做一次 n = n & (n - 1) 的操作会使得二进制数少一个最低位上的 1。
特别的,二进制数中只有一个 1 的时候,n & (n - 1) // == 0。由此 n > 0 && (n & (n - 1)) 也常用于判断整数 n 是不是 2 的指数:
function isPowerOfTwo(n){
// better judge if n is an int at first..
if(n <= 0) return false;
return !(n&(n-1));
}
关于 JS 中整数的判断,ES5 及以前请看 How to check if a variable is an integer in JavaScript? @SO,ES6 及以后可以用 Number.isInteger()。
相关补充
刚好最近在看《Effective JavaScript》这本书,书中第二条——“理解 JavaScript 的浮点数”,有一些相关知识。
JS 中的数字
JavaScript 中的数字(number)都是 64 位双精度浮点数,即 double。JS 中的整数仅仅是其一个子集,整数的范围在 [-2^53, 2^53]。
Safe Integer
Safe integer 是符合如下描述的整数:
- 能被精确地表示为一个 IEEE-754 双精度浮点数
- 这个表示不能是其他整数的舍入结果
所以,2^53 虽然能被 IEEE-754 双精度浮点数精确表示,但是由于 2^53 + 1 在向零舍入和就近舍入中会被舍入为 2^53 ,所以不符合 safe integer 的要求,用 Number.isSafeInteger 判断会得到 false :
JS 中的位运算
位运算符的工作原理:
标准的 JS 浮点数 =隐式转换=> 32 位的有符号整数 =做位运算后返回=> 标准的 JS 浮点数
说到 32 位有符号整数,比较容易想到 C 语言中的 int 类型。那么也就稍微可以理解下题目中给出的 x 和 y 的范围 [0,2^31) ( 32 位有符号整数的非负整数范围)了。
小结
这虽然是 leetcode 上最简单的一道题目,但是我还是有所收获,特别是对 二进制数中 1 的个数的求解方法。