题目描述
在一个游戏中有n个英雄,初始时每个英雄受到数值为ai的伤害,每个英雄都有一个技能“折射”,即减少自己受到的伤害,并将这部分伤害分摊给其他人。对于每个折射关系,我们用数对\((x_i,y_i,z_i)\)来表示\(x_i\)将自己受到伤害去掉\(z_i\)的比例,将这些伤害转移给\(y_i\)(\(x_i,y_i\)是整数,\(z_i\)是实数)。
求出经过反复折射后最后每个英雄受到的实际总伤害。
输入格式
第一行一个正整数:\(n\),表示有\(n\)个英雄,第二行\(n\)个整数\(A_i\),依次表示每个英雄受到的初始伤害。第三行一个正整数\(m\),表示有\(m\)对折射关系。接下来\(m\)行,每行三个数\(x_i,y_i,z_i\),表示\(x_i\)将自己受到伤害去掉\(z_i\)的比例,将这些伤害转移给\(y_i\)。
输出格式
输出\(n\)行,第\(i\)行表示第\(i\)个英雄最后受到的实际总伤害。保留六位小数。
样例
样例输入
3
1 0 2
3
1 2 0.3000
1 2 0.2000
2 1 0.5000样例输出
0.666667
0.333333
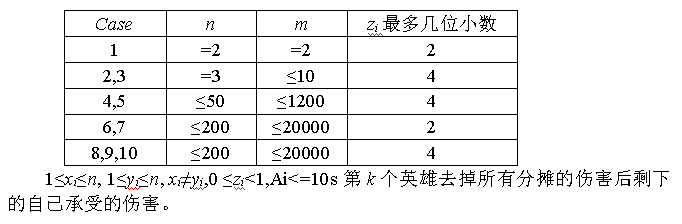
2.000000数据范围
题解
设\(D_i\)为分摊伤害后\(i\)最终受到的伤害,\(C_i\)为\(i\)自己真实受到的的伤害占总伤害的比例,\(T_{i,j}\)表示\(i\)总共分给\(j\)的伤害的比例。
那么\(D_i\)中除了第一次天降的伤害\(A_i\),其他伤害都是来源于别人的分摊,那么可以很轻松地推出一个式子:
\[\frac{D_i}{C_i}=\sum_{j≠i}\frac{D_j}{C_j}\cdot T_{j,i}+A_i\]
直接按照这个式子建立关于\(D_i\)的方程组,然后高斯消元解方程即可。
\(Code:\)
#include
#include
#include
#include
#include
using namespace std;
#define N 205
#define M 20005
#define eps 1e-6
int n, m, A[N];
long double val[N][N], mat[N][N];
long double ans[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++)
scanf("%d", &A[i]), val[i][i] = 1;
int x, y;
double c;
scanf("%d", &m);
for (int i = 1; i <= m; i++)
{
scanf("%d%d%lf", &x, &y, &c);
val[x][y] += c;
val[x][x] -= c;
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
if (i != j)
mat[i][j] = -val[j][i] / val[j][j];
mat[i][i] = 1 / val[i][i];
mat[i][n + 1] = -A[i];
}
for (int i = 1; i <= n; i++)
{
for (int j = i + 1; j <= n; j++)
if (fabs(mat[j][i]) > eps)
{
for (int k = i; k <= n + 1; k++)
swap(mat[i][k], mat[j][k]);
break;
}
long double s = mat[i][i];
for (int j = i; j <= n + 1; j++)
mat[i][j] /= s;
for (int j = i + 1; j <= n; j++)
{
s = mat[j][i];
for (int k = i; k <= n + 1; k++)
mat[j][k] -= s * mat[i][k];
}
}
ans[n + 1] = 1;
for (int i = n; i >= 1; i--)
for (int j = i + 1; j <= n + 1; j++)
ans[i] -= mat[i][j] * ans[j];
for (int i = 1; i <= n; i++)
printf("%.6lf\n", double(ans[i]));
}