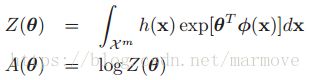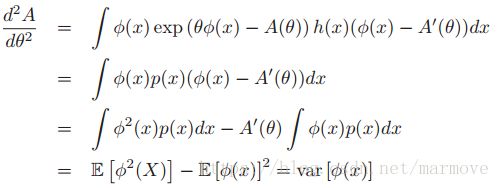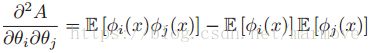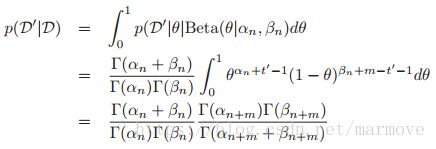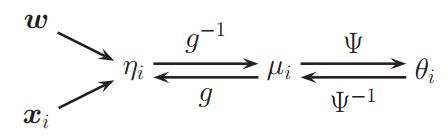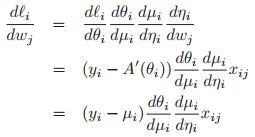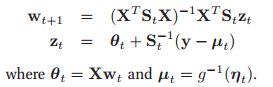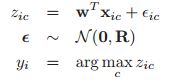MLAPP————第九章 广义线性模型和指数家族
第九章 广义线性模型和指数家族
9.1 简介
我们现在已经遇到了许多不同的概率分布,如:高斯分布,伯努利分布,学生t分布,均匀分布,gamma分布等。其实在这些分布里面,有很多的分布其实是属于一个分布家族,这个家族就叫做指数家族(exponential family)。在这一章节中,我们主要就是讨论指数家族分布的一些性质。
9.2 指数家族
在我们进行正式的定义指数家族之前,我们先说明一下它为什么这么重要的理由:
1. 在一定的规则条件下,是唯一一个有有限的充分统计量的家族(有限的指充分统计量的数目并不随着数据量的增加而增加),这意味着我们可以把数据压缩到归纳到一个有限的统计量集合而不丢失任何的信息。对于在线学习这个是非常有用的。
2. 指数家族是唯一一个存在共轭先验的这样一个分布家族,这样可以大大简化后验分布的计算 (Sec. 9.2.5)。
3. 指数族可以被证明是在用户选择的某些约束条件下,能够做出假设最少的分布族 (Sec. 9.2.6)。
4. 指数家族是广义线性模型的核心 (Sec. 9.3)。
5. 指数家族是变分推理的核心 (Sec. 21.2)。
9.2.1 定义
对于一个pdf或者pmf![]() 而言,其中
而言,其中![]() ,并且有
,并且有![]() ,如果它具有以下的形式,就被称之为指数家族:
,如果它具有以下的形式,就被称之为指数家族:
其中![]() 称之为自然参数(natural parameters)或者是典范参数(canonical parameters),
称之为自然参数(natural parameters)或者是典范参数(canonical parameters),![]() 称为充分统计量(sufficient statistics),
称为充分统计量(sufficient statistics),![]() 称之为配分函数(partition function),
称之为配分函数(partition function),![]() 称之为 log partition function或者是cumulant function(累积量函数)。
称之为 log partition function或者是cumulant function(累积量函数)。![]() 是一个标量,我们一般设置为1,如果说
是一个标量,我们一般设置为1,如果说![]() ,我们就说它是一个自然的指数家族。
,我们就说它是一个自然的指数家族。
书中的9.2式子也可以被写作![]() ,其中
,其中![]() ,如果说
,如果说![]() 这个就叫做curved exponential family,这意味着相比于参数我们有更多的统计量。如果
这个就叫做curved exponential family,这意味着相比于参数我们有更多的统计量。如果![]() ,那么这个模型就被称之为规范形式,我们接下来的模型在不加说明的情况下都是规形式。
,那么这个模型就被称之为规范形式,我们接下来的模型在不加说明的情况下都是规形式。
9.2.2 例子
下面我们来举一些具体的例子帮助理解上面的定义
9.2.2.1 伯努利
在伯努利分布中,我们有![]() ,那么它的分布可以被写成如下的指数家族的形式:
,那么它的分布可以被写成如下的指数家族的形式:
![]()
其中![]() 。但是这样的表示不是最简的,因为有一个性质我们没用到那就是
。但是这样的表示不是最简的,因为有一个性质我们没用到那就是![]() ,所以说我们把伯努利分布换一种形式来写:
,所以说我们把伯努利分布换一种形式来写: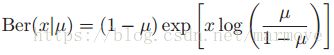 ,这样我们就有
,这样我们就有![]() 并且
并且![]() ,我们可以将均值参数从规范参数中恢复即:
,我们可以将均值参数从规范参数中恢复即:![]()
9.2.2.2 多分类分布(Multinoulli)
multinoulli 可以被写成如下的形式:
其中![]() ,那么对应到指数家族的形式就是如下:
,那么对应到指数家族的形式就是如下:![]() ,其中我们有:
,其中我们有:
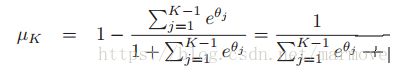 ,因此
,因此 ,如果我们定义
,如果我们定义![]() ,那么我们有
,那么我们有![]() ,其中
,其中![]() 是softmax function。这个就不是minimal的情况了。
是softmax function。这个就不是minimal的情况了。
9.2.2.3 单变量的高斯
单变量的高斯模型也可以被写成指数家族的形式:
9.2.2.4 非指数家族分布
并不是所有的分布都可以写成指数家族的形式,比如均匀分布,学生t分布就不是指数家族的。
9.2.3 Log partition function
对于指数家族来说有一个重要的性质就是关于log partition 函数的导数就是充分统计量的累计量,所以说有时候也叫做累积函数。那么什么是累积量呢,之前我们都学过中心矩,这是统计量的一种,在统计方面,累积量可以比矩更具有优势,每个独立随机变量之和的累积量是加数的相应累积量的总和。那么一阶累积量就是E[X],二阶的累积量就是var[X]。下面我们将对与1维的情况进行证明,二维的情况就直接给出结论。
我们有:
9.2.3.1 例子:伯努利分布
比如我们来看伯努利分布,其中![]() ,所以说我们有先求个一阶导数:
,所以说我们有先求个一阶导数: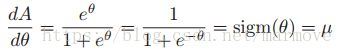 ,再求个二阶导:
,再求个二阶导: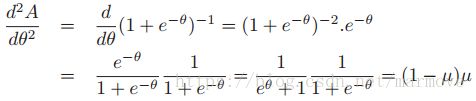 。
。
9.2.4 关于指数家族的MLE
指数家族的似然具有如下的形式: ,其中充分统计量为N以及
,其中充分统计量为N以及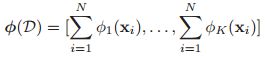 ,对于伯努利分布是
,对于伯努利分布是![]() ,对于高斯分布是
,对于高斯分布是![]() 。一个叫做Pitman-Koopman-Darmois theorem的理论表明,在某些规则条件下,指数家族是唯一一个拥有有限充分统计量的家族。这里的有限指统计量的数目并不随着N的增加而增加。
。一个叫做Pitman-Koopman-Darmois theorem的理论表明,在某些规则条件下,指数家族是唯一一个拥有有限充分统计量的家族。这里的有限指统计量的数目并不随着N的增加而增加。
关于这个理论的其中的一个条件就是分布的支撑集合(也就是使得分布不为0的定义区间)应该是不依赖于参数的。举个简单的例子,均匀分布中:![]() ,这个的支撑集合明显是依赖于参数的,所以不是指数家族的。
,这个的支撑集合明显是依赖于参数的,所以不是指数家族的。
下面我们描述一下如何来计算关于规范指数家族模型的MLE。给定N个独立的数据点![]() ,那么log似然就是:
,那么log似然就是:
![]() ,我们知道
,我们知道![]() 是一个凹函数,而
是一个凹函数,而![]() 又是一个线性的函数,所以整体来说就是一个凹函数,那么这个最优解是唯一的。关于这个函数的梯度:
又是一个线性的函数,所以整体来说就是一个凹函数,那么这个最优解是唯一的。关于这个函数的梯度:
![]() ,令梯度为0的话,
,令梯度为0的话,![]() 必须满足
必须满足 (这个左右两边都是向量),这个就叫做矩匹配,例如对于伯努利分布,
(这个左右两边都是向量),这个就叫做矩匹配,例如对于伯努利分布,![]()
![]() ,因此MLE满足
,因此MLE满足 。
。
9.2.5 关于指数家族的贝叶斯*
我们在贝叶斯分析中知道,如果我们对于一个似然函数能够找到它的共轭先验,那么整个的后验计算会非常的简单。而有共轭先验就要意味着我们的似然函数和先验函数具有相同的形式。从这一点上来说,我们的似然函数必须拥有有限的充分统计量,因此我们可以得到:![]() (这就说明了,关于数据的分布与关于数据充分统计量的分布是一样的,这样意味着我们能够找到一个具有固定参数的先验),这同时也表明了只有指数家族才具有共轭先验。接下来我们就要具体的进行先验和后验的推导。
(这就说明了,关于数据的分布与关于数据充分统计量的分布是一样的,这样意味着我们能够找到一个具有固定参数的先验),这同时也表明了只有指数家族才具有共轭先验。接下来我们就要具体的进行先验和后验的推导。
9.2.5.1 似然
指数家族的似然函数具体如下:![]() ,其中
,其中![]() ,如果是在规范参数下的话,那么似然函数就可以变为:
,如果是在规范参数下的话,那么似然函数就可以变为:![]() ,其中
,其中![]() 。
。
9.2.5.2 先验
比较自然的先验具有如下的形式:![]() ,如果将其写作标准形式的话,那就是:
,如果将其写作标准形式的话,那就是:![]() ,其中
,其中![]() 。
。
9.2.5.3 后验
根据刚才写的似然和共轭先验,![]() ,其实就是对于超参数进行了相加的操作。在规范形式下,就是
,其实就是对于超参数进行了相加的操作。在规范形式下,就是 。
。
9.2.5.4 后验密度预测
接下来,我们要根据之前的数据![]() 来对未来的数据
来对未来的数据![]()
![]() 进行预测。为了符号的简单,我们要对充分统计量进行符号的简化:
进行预测。为了符号的简单,我们要对充分统计量进行符号的简化:![]() ,
,![]() ,因此先验的形式就变成了:
,因此先验的形式就变成了:![]() ,似然和后验具有相似的形式,所以我们有(这里把未来的数据当作变量来看):
,似然和后验具有相似的形式,所以我们有(这里把未来的数据当作变量来看):
如果N=0,就跟我们之前推导的后验是一样的了。
9.2.5.5 例子:伯努利分布
我们再次选取一个简单的例子beta-bernoulli分布。
在规范形式下,似然函数为: ,因此共轭先验的形式为:
,因此共轭先验的形式为: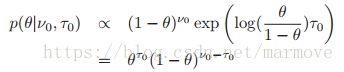 ,如果我们定义
,如果我们定义![]() 以及
以及![]() ,我们可以看到这就是Beta分布。然后后验具体的分布如下:
,我们可以看到这就是Beta分布。然后后验具体的分布如下: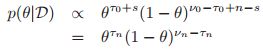 ,其中
,其中![]() 。
。
我们再来看后验密度预测,假设![]() ,且令
,且令![]() 为过去数据中正面朝上的次数。我们可以估计对于未来的数据
为过去数据中正面朝上的次数。我们可以估计对于未来的数据![]() 的概率分布,并且
的概率分布,并且![]()
![]() ,如下:
,如下:
其中:
9.2.6 关于指数分布的最大熵的推导*
尽管我们都知道指数家族是非常的有用和方便的,那么有没有关于指数家族更加深入的理解呢。其实指数家族是在用户指定一组特定的约束的条件下,所需要做出假设最少的分布。事实上,假设我们只知道期望值或者是某些特征或者是函数值,即我们知道:
![]() ,其中呢
,其中呢![]() 是一些已知的常数,
是一些已知的常数,![]() 是任意的一个函数,我们就要在这样的一个限制下找到一个使得熵最大的分布。那么我们的分布要满足上面的约束,同时也要满足概率分布的基本约束
是任意的一个函数,我们就要在这样的一个限制下找到一个使得熵最大的分布。那么我们的分布要满足上面的约束,同时也要满足概率分布的基本约束![]() ,所以说我们使用拉格朗日乘子法,那么我们的目标函数可以写为:
,所以说我们使用拉格朗日乘子法,那么我们的目标函数可以写为:![]() ,那么接下来我们就要对
,那么接下来我们就要对![]() 进行求导,我们假设
进行求导,我们假设![]() 是离散分布的,这样
是离散分布的,这样![]() 就是一个向量,那么求导的结果就是:
就是一个向量,那么求导的结果就是:![]() ,我们令
,我们令![]() ,那么就可以得到
,那么就可以得到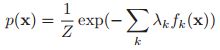 ,其中
,其中![]()
所以说具有指数家族分布的形式。所以说指数分布就是满足上面说的这些条件的最大熵分布。
9.3 广义线性模型(Generalized linear models, GLMs)
线性回归和logistic回归都是广义线性模型(generalized linear models, GLMs)的一种。在这些模型当中,输出的概率密度模型都是指数家族的。其中均值是输入的线性组合再经过一个非线性的函数。接下来我们将详细的讨论GLMs,为了符号的简单,我们的输出是标量的形式。
9.3.1 基本要素
为了理解GLMs,我们首先考虑在标量情况下的非条件分布的情况,也是属于指数家族分布的,具体如下:
其中![]() 是扩散参数(dispersion parameter,经常设置为1),
是扩散参数(dispersion parameter,经常设置为1),![]() 是自然参数。A是配分函数,c是一个归一化常数,因为我们这里关注的是均值,所以
是自然参数。A是配分函数,c是一个归一化常数,因为我们这里关注的是均值,所以![]() 可以看做是一个常量。例如,在logistic回归中,
可以看做是一个常量。例如,在logistic回归中,![]() 是log-odds ratio,即
是log-odds ratio,即![]() ,其中
,其中![]() (具体见9.2.2.1)。为了把均值参数变换到自然参数,我们可以使用函数
(具体见9.2.2.1)。为了把均值参数变换到自然参数,我们可以使用函数![]() ,所以
,所以![]() 。这个函数是由指数家族分布的定义唯一确定的。事实上,我们同样也会有
。这个函数是由指数家族分布的定义唯一确定的。事实上,我们同样也会有![]() 。另外我们从9.2.3中知道均值其实是配分函数的导数,所以我们有
。另外我们从9.2.3中知道均值其实是配分函数的导数,所以我们有![]() 。
。
现在我们来添加输入,我们现在定义一个线性函数作为我们的输入:![]() ,现在我们把分布的均值设为这个线性组合的可逆单调函数。我们把这个函数称之为均值函数,记作
,现在我们把分布的均值设为这个线性组合的可逆单调函数。我们把这个函数称之为均值函数,记作![]() ,于是我们有
,于是我们有![]() ,下图给出了这样的模型的基本图解:
,下图给出了这样的模型的基本图解:
我们称![]() 为联系函数。我们几乎可以选择任意的函数
为联系函数。我们几乎可以选择任意的函数![]() ,只要它是可逆的,并且
,只要它是可逆的,并且![]() 的取值范围是合适的。例如在logistic回归中,我们设置
的取值范围是合适的。例如在logistic回归中,我们设置![]() 。
。
一个简单的选取link function的方法就是选择![]() ,这个叫做规范的link function。在这样的情况下,我们有
,这个叫做规范的link function。在这样的情况下,我们有![]() ,所以我们的模型就是:
,所以我们的模型就是:
在下面的表中,我们一些常见的分布的规范的link function:
根据9.2.3的结果,可以看出,响应变量的均值和方差如下:
下面举几个具体的例子:
因此我们有:![]() 。
。
对于泊松分布,我们有:
![]()
![]()
![]() 。泊松回归广泛应用于生物统计学。
。泊松回归广泛应用于生物统计学。
9.3.2 ML和MAP估计
GLMs的一个吸引人的特性是,它们可以使用与logistic回归完全相同的方法进行拟合(因为logistic回归其实就是广义线性模型的一种)。事实上,log似然函数具有如下的形式:
那么我们可以利用链式法则对![]() 进行求导:
进行求导:
如果我们使用规范形式,即![]() ,那么我们就有:
,那么我们就有: ,其实有了梯度之后,我们就可以使用梯度下降法了,这在8.5.2讨论过。但是为了提高效率,我们可以使用牛顿法,那么我们就需要就算汉森矩阵,如果使用规范形式,那么:
,其实有了梯度之后,我们就可以使用梯度下降法了,这在8.5.2讨论过。但是为了提高效率,我们可以使用牛顿法,那么我们就需要就算汉森矩阵,如果使用规范形式,那么:
 ,其中
,其中![]() ,我们可以借鉴IRLS的方法(8.3.4),那么牛顿更新步骤就可以写为:
,我们可以借鉴IRLS的方法(8.3.4),那么牛顿更新步骤就可以写为:
如果我们将推导扩展到处理非规范link function,我们会发现汉森矩阵有另一个项。然而,结果表明,汉森矩阵的期望与式子9.92是一样的。使用期望的汉森矩阵(被称为fisher信息矩阵)而不是实际的汉森矩阵被称为Fisher scoring method。
我们可以直接修改上面的过程,使用高斯先验来进行MAP,我们只修改目标、梯度和汉森矩阵,就像我们在8.3.6节的logistic回归中加入l2正则化一样。
9.3.3 贝叶斯推理
广义线性模型的贝叶斯推理,我觉得现在大可不必探讨这一块,关于这一块,后面会慢慢接触到。在8.4中,我们讲了如何做高斯近似,当然具体的更复杂的方法后面会慢慢接触到。
9.4 probit 回归
在logistic回归中,我们使用的是这样的模型:![]() 。实际上我们可以使用任何的函数
。实际上我们可以使用任何的函数![]() ,只要这个函数呢能够从
,只要这个函数呢能够从![]() 映射到
映射到![]() ,这个时候
,这个时候![]() ,在下表中,我们给出了符合这个条件的一些函数:
,在下表中,我们给出了符合这个条件的一些函数:
在这一节中呢,我们关注于![]() ,其中
,其中![]() 是高斯分布的cdf。这个就称之为probit regression。probit函数和sigmoid函数其实长得是差不多的,但是probit回归相比于logistic回归也还是会有一些好处的。
是高斯分布的cdf。这个就称之为probit regression。probit函数和sigmoid函数其实长得是差不多的,但是probit回归相比于logistic回归也还是会有一些好处的。
9.4.1 使用梯度下降优化的方法进行ML/MAP估计
使用标准的梯度下降法,我们可以得到probit回归的MLE。书中说令![]() ,注意这里
,注意这里![]() 和我们之前说的均值并不是一个东西,只是一个标号而已。另外
和我们之前说的均值并不是一个东西,只是一个标号而已。另外![]() ,那么对于某一个数据log似然的梯度是:
,那么对于某一个数据log似然的梯度是:
其中![]() 是标准正态分布的pdf,
是标准正态分布的pdf,![]() 是它的cdf。同样的,我们可以得到我们的汉森矩阵是:
是它的cdf。同样的,我们可以得到我们的汉森矩阵是:
。
上面这是ML的这样一个梯度和汉森,对于MAP而言,其实是差不多的,尤其是加了共轭先验,没太大区别,如果我们的先验是:
![]() ,那么相应的梯度和汉森矩阵就是:
,那么相应的梯度和汉森矩阵就是:![]() 。
。
9.4.2 隐变量的解释
下面我们可以解释我们的probit(以及logistic)模型。首先,我们对于每一组数据![]() 引入两个与它相关的隐变量
引入两个与它相关的隐变量![]() 对应于
对应于![]() 以及
以及![]() 的可能性。
的可能性。
那么我们最后观察到的y的数据就是取决于这两个隐变量哪一个更大,即具体如下:
其中![]() 表明的是误差项,表示一些其它的因素可能会对模型产生的影响。这个叫做随机效用模型(random utility model RUM)。
表明的是误差项,表示一些其它的因素可能会对模型产生的影响。这个叫做随机效用模型(random utility model RUM)。
我们定义一个新的变量![]() ,其中
,其中![]() ,如果
,如果![]() 是一个高斯分布的话,那么两个高斯随机变量的差也是高斯分布。所以我们可以有如下公式:
是一个高斯分布的话,那么两个高斯随机变量的差也是高斯分布。所以我们可以有如下公式:
我们称这个叫做difference RUM 或者 dRUM模型。当我们把隐变量积分掉之后,就得到的是probit模型:
这样的解释就非常的物理,之前的就很数学,之前只要求映射是对的就可以,这里解释了为什么用不同的映射,这取决于这边的误差项的分布。
有趣的是,如果这里我假设![]() 的分布是gunbel分布,那么其实就对应于logistic回归的模型。
的分布是gunbel分布,那么其实就对应于logistic回归的模型。
9.4.3 有序的probit回归*
利用隐变量解释probit回归的一个优点是容易易于推广到有序回归的情况,即输出变量的值可以取C个离散值,这些离散值可以以某种方式排序,如低、中、高,这就是有序回归。
基本的思想如下。我们引出C+1个阈值![]() ,然后设定
,然后设定![]() ,其中
,其中![]() 。
。
但是关于这个模型的MLE计算会比较棘手,因为我们需要为![]() 和
和![]() 优化,而且后者必须服从一个排序约束(因为之前就要设定好
优化,而且后者必须服从一个排序约束(因为之前就要设定好![]() 的内部的顺序)。
的内部的顺序)。
9.4.4 Multinomial probit 模型*
我们现在考虑相应y的值有C种,但是与我们上面的有序回归模型相比,这C个值是平等的没有等级之分的。Multinomial probit 模型定义如下:
我更偏向于第一个式子写成![]() ,当然对于书上的定义我们有:
,当然对于书上的定义我们有:![]() 。当然如果我们不使用
。当然如果我们不使用![]() ,我们如果输出的
,我们如果输出的![]() 是个C维的向量,那么就可以用
是个C维的向量,那么就可以用![]() ,对于这个模型我们称之为multivariate probit。
,对于这个模型我们称之为multivariate probit。
9.5 多任务的学习
有时,我们希望去拟合很多相关的分类或者是回归模型。对于这种情况,我们假设所有的模型的输入输出的映射是相似的是很合理的。所以我们有可能会获得更好的性能同时去估计这些所有的参数,而不是一个个的去估计。在机器学习中,这个叫做多任务学习(multi-task learning)或者是transfer learning 或learning to learn。在统计贝叶斯中,这通常使用层次贝叶斯模型来解决,我们下面将会讨论这个方法。当然也有一些其它的方法可以解决这个问题。
9.5.1 关于多任务学习的多层贝叶斯
令![]() 是第
是第![]() th个组第
th个组第![]() th物体的输出,其中
th物体的输出,其中![]() ,
,![]() 。例如j可能指的是第j个学校,而i则是指的是这个学校的第i个学生。令
。例如j可能指的是第j个学校,而i则是指的是这个学校的第i个学生。令![]() 是与
是与![]() 相关的特征向量。那我们的目的就是去计算所有的
相关的特征向量。那我们的目的就是去计算所有的![]() ,对于所有的j,这个就是上面所说的多任务模型。
,对于所有的j,这个就是上面所说的多任务模型。
就是有时会出现这样一个情况有些组数据很多,但是大量的组其实数据量都很少。因此我们并不希望对所有的组完全分开来去做,但是我们也并不希望对于所有的组都只使用同样的模型。作为一种折衷,我们可以为每个组适合一个单独的模型,但是鼓励模型参数在组之间是相似的。更详细的说明就是,假设是在GLM的模型下,那么我们有![]() ,其中g为link函数,我觉得这里写错了,前面那个应该是
,其中g为link函数,我觉得这里写错了,前面那个应该是![]() ,这样的话对于参数
,这样的话对于参数![]() ,我们其实是有一个先验的,对于任意的组都是有的,如果是这样的话,那么每一个都是独立的了,所以我们为了让所有的参数具有一定的相似性,我们假设每一个组的参数
,我们其实是有一个先验的,对于任意的组都是有的,如果是这样的话,那么每一个都是独立的了,所以我们为了让所有的参数具有一定的相似性,我们假设每一个组的参数![]() 也都服从一个相同的先验
也都服从一个相同的先验![]() 。这样的话,那些数据量小的组在进行参数估计的时候就会借用到数据量大的组。因为
。这样的话,那些数据量小的组在进行参数估计的时候就会借用到数据量大的组。因为![]() 是一个固定的值,所以说关于这个值的确定是用到所有的数据,这样就联系起来了。(5.5详细的讲了关于这个模型的计算)
是一个固定的值,所以说关于这个值的确定是用到所有的数据,这样就联系起来了。(5.5详细的讲了关于这个模型的计算)
假设为了简单起见,我们设![]() ,并且
,并且![]() 和
和![]() 都是已知的。那么log似然函数具有如下的形式:
都是已知的。那么log似然函数具有如下的形式:
我们可以使用标准的梯度下降法,对整个后验进行MAP估计。当然我们也可以使用迭代的方法,对每一个参数依次的利用梯度下降法进行估计。由于先验和似然都是凸的,所以能够保证收敛到最优解。最终我们把所有的参数都估计出来之后就可以对每一个模型单独的进行使用了,他们之间就完全不相关了。
9.5.2 关于个性化垃圾邮件过滤的应用
关于多任务学习的一个有趣的应用就是个性化的垃圾邮件过滤。假设我们希望针对每一个人制定一个垃圾邮件过滤模型,类似于上面用参数![]() 刻画。如果我们对每一个用户去单独的去估计
刻画。如果我们对每一个用户去单独的去估计![]() 是很困难的。所以同样,我们假设每个参数服从一个先验
是很困难的。所以同样,我们假设每个参数服从一个先验![]() 。
。
在这里我们利用一个小的技巧对模型进行估计,我们把整体的数据copy成两份,那么:
![]() ,这个也很好理解,就是先验加上似然,针对每一个用户那么
,这个也很好理解,就是先验加上似然,针对每一个用户那么![]()
![]() (外面的转置应该放到里面去)。其中
(外面的转置应该放到里面去)。其中![]() 是从所有人的email中估计的,而
是从所有人的email中估计的,而![]() 则是从各自用户的数据中估计得到的。我们假设问题的模型也是上一节中的多层贝叶斯,那么
则是从各自用户的数据中估计得到的。我们假设问题的模型也是上一节中的多层贝叶斯,那么![]() ,因为这里在定义的时候这里是没有把先验放进去的。那么原始模型的对数概率可以重写为:
,因为这里在定义的时候这里是没有把先验放进去的。那么原始模型的对数概率可以重写为:
如果这里![]() ,那么就跟对整个参数加了正则项是一样的,如果把
,那么就跟对整个参数加了正则项是一样的,如果把![]() 整体看做参数的话,但是往往它们不相等能够获得更好的性能。
整体看做参数的话,但是往往它们不相等能够获得更好的性能。
9.5.3 应用于领域适应(domain adaptation)
领域适配是对来自不同分布的数据(如电子邮件和新闻专线文本)训练一组分类器的问题。这个问题显然是多任务学习的一个特例,任务是相同的。
(Finkel and Manning 2009)利用上述层次贝叶斯模型对两个NLP任务进行域自适应,命名为实体识别和解析。他们报告了相对于将独立模型拟合到每个数据集的较大改进,以及相对于汇集所有数据和拟合单个模型的方法的较小改进。
9.5.4 其它种类的先验
在多分类的问题中,比较常见的是假设先验是高斯的。然而,有时其它的先验会更加的适合。考虑一个联合分析的任务,需要我们找出消费者对产品的哪一个特性是最喜欢的。这个我们同样可以使用多层贝叶斯去做,但是这里使用的就不是高斯的先验,而是使用的是sparsity-promoting prior。
就是说假设所有的模型都是相似的的,有时候并不是好的假设,有时候部分之间的相似性其实是并不太一样的,所以这个时候我们可能需要使用更加复杂的先验,比如说混合的高斯模型等等。
9.6 广义线性混合模型*
假设我们推广多任务学习的场景,对于每个输出![]() ,不仅要有数据
,不仅要有数据![]() ,同时还要有只和group相关的数据
,同时还要有只和group相关的数据![]() 。相似的,我们的参数也是分为每一个组上相关的,
。相似的,我们的参数也是分为每一个组上相关的,![]() ,另一个参数就是体现组之间关系的参数
,另一个参数就是体现组之间关系的参数![]() 。
。