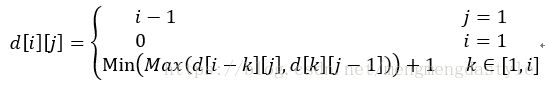算法之动态规划（Dynamic Programming）

1、介绍

（1）
　　动态规划是解决多阶段决策过程最优化的一种有效的数学方法，他是美国学者Richard.bellman在1951年提出的，1957年他的专著《动态规划》的问世标志着运筹学的一个重要分支—-动态规划的诞生。
　　所谓多阶段决策问题是指这样一类问题，该问题的决策过程时一种在多个相互联系的阶段分别作出决策以形成序列决策的过程，而这些决策均是根据总体最优化这一共同的目标而采取的。
　　基本思想：
　　把一个较复杂的问题按照阶段划分，分解为若干个较小的局部问题，然后按照局部问题的递推关系，依次作出一系列决策，直至整个问题达到总体最优的目标。
（2） 动态规划包含三个重要的概念：
- 最优子结构
- 边界
- 状态转移方程
（3）解题的一般步骤是：
1. 找出最优解的性质，刻画其结构特征和最优子结构特征；
2. 递归地定义最优值，刻画原问题解与子问题解间的关系；
3. 以自底向上的方式计算出各个子问题、原问题的最优值，并避免子问题的重复计算；
4. 根据计算最优值时得到的信息，构造最优解。
（4）使用动态规划特征：
1. 求一个问题的最优解
2. 大问题可以分解为子问题，子问题还有重叠的更小的子问题
3. 整体问题最优解取决于子问题的最优解（状态转移方程）
4. 从上往下分析问题，从下往上解决问题
5. 讨论底层的边界问题

２、最长公共子序列（LCS）与最长公共子串(DP)

（1）有两个母串：
　 A B C B D A B
　B D C A B A
　　公共子序列：在母串中都出现过并且出现顺序与母串保持一致。
　　最长公共子序列（Longest Common Subsequence,LCS），顾名思义，是指在所有的子序列中最长的那一个。
　　子串：是要求更严格的一种子序列，要求在母串中连续地出现。
（2）求解最长公共子序列
　　对于母串Ｘ＝＜x1,x2,⋯,xm＞, Y=＜y1,y2,⋯,yn＞，求LCS与最长公共子串。
　　动态规划
　　假设Z=＜z1,z2,⋯,zk＞是X与Y的LCS， 我们观察到
　　如果Xm=Yn，则Zk=Xm=Yn，有Zk−1是Xm−1与Yn−1的LCS；
　　如果Xm≠Yn，则Zk是Xm与Yn−1的LCS，或者是Xm−1与Yn的LCS。
　　因此，求解LCS的问题则变成递归求解的两个子问题。但是，上述的递归求解的办法中，重复的子问题多，效率低下。改进的办法——用空间换时间，用数组保存中间状态，方便后面的计算。这就是动态规划（DP)的核心思想了。
　　DP求解LCS
　　用二维数组ci记录串x1x2⋯xi与y1y2⋯yj的LCS长度，则可得到状态转移方程。

x: A  B  C  B  D  A  B
y: B  D  C  A  B  A

最长公共子序列：BDAB
             BCAB 
             BCBA

代码实现：

public static int lcs(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                c[i][j] = c[i-1][j-1] + 1;  
            } else {  
                c[i][j] = max(c[i - 1][j], c[i][j - 1]);  
            }  
        }  
    }  
    return c[len1][len2];  
}

（2）求解最长公共子串

转移方程：

　　最长公共子串的长度为 max(c[i,j]), i∈{1,⋯,m},j∈{1,⋯,n}。

代码实现：

public static int lcs(String str1, String str2) {  
    int len1 = str1.length();  
    int len2 = str2.length();  
    int result = 0;     //记录最长公共子串长度  
    int c[][] = new int[len1+1][len2+1];  
    for (int i = 0; i <= len1; i++) {  
        for( int j = 0; j <= len2; j++) {  
            if(i == 0 || j == 0) {  
                c[i][j] = 0;  
            } else if (str1.charAt(i-1) == str2.charAt(j-1)) {  
                c[i][j] = c[i-1][j-1] + 1;  
                result = max(c[i][j], result);  
            } else {  
                c[i][j] = 0;  
            }  
        }  
    }  
    return result;  
} 

３、背包问题

（1）问题
　　假设现有容量10kg的背包，另外有3个物品，分别为a1，a2，a3。物品a1重量为3kg，价值为4；物品a2重量为4kg，价值为5；物品a3重量为5kg，价值为6。将哪些物品放入背包可使得背包中的总价值最大？
（2）思路
　　先将原始问题一般化，欲求背包能够获得的总价值，即欲求前i个物体放入容量为m（kg）背包的最大价值ci——使用一个数组来存储最大价值，当m取10，i取3时，即原始问题了。而前i个物体放入容量为m（kg）的背包，又可以转化成前(i-1)个物体放入背包的问题。下面使用数学表达式描述它们两者之间的具体关系。
　　
　　表达式中各个符号的具体含义。

　　w[i] :  第i个物体的重量；
　　p[i] : 第i个物体的价值；
　　c[i][m] ： 前i个物体放入容量为m的背包的最大价值；
　　c[i-1][m] ： 前i-1个物体放入容量为m的背包的最大价值；
　　c[i-1][m-w[i]] ： 前i-1个物体放入容量为m-w[i]的背包的最大价值；
　　由此可得：
　　　　　　c[i][m]=max{c[i-1][m-w[i]]+pi , c[i-1][m]}

代码实现：

public class Pack01 {

    public int [][] pack(int m,int n,int w[],int p[]){
        //c[i][v]表示前i件物品恰放入一个重量为m的背包可以获得的最大价值
        int c[][]= new int[n+1][m+1];
        for(int i = 0;i1;i++)
            c[i][0]=0;
        for(int j = 0;j1;j++)
            c[0][j]=0;
        //
        for(int i = 1;i1;i++){
            for(int j = 1;j1;j++){
                //当物品为i件重量为j时，如果第i件的重量(w[i-1])小于重量j时，c[i][j]为下列两种情况之一：
                //(1)物品i不放入背包中，所以c[i][j]为c[i-1][j]的值
                //(2)物品i放入背包中，则背包剩余重量为j-w[i-1],所以c[i][j]为c[i-1][j-w[i-1]]的值加上当前物品i的价值
                if(w[i-1]<=j){
                    if(c[i-1][j]<(c[i-1][j-w[i-1]]+p[i-1]))
                        c[i][j] = c[i-1][j-w[i-1]]+p[i-1];
                    else
                        c[i][j] = c[i-1][j];
                }else
                    c[i][j] = c[i-1][j];
            }
        }
        return c;
    }
    /**
     * 逆推法求出最优解
     * @param c
     * @param w
     * @param m
     * @param n
     * @return
     */
    public int[] printPack(int c[][],int w[],int m,int n){

        int x[] = new int[n];
        //从最后一个状态记录c[n][m]开始逆推
        for(int i = n;i>0;i--){
            //如果c[i][m]大于c[i-1][m]，说明c[i][m]这个最优值中包含了w[i-1](注意这里是i-1，因为c数组长度是n+1)
            if(c[i][m]>c[i-1][m]){
                x[i-1] = 1;
                m-=w[i-1];
            }
        }
        for(int j = 0;jreturn x;
    }
    public static void main(String args[]){
        int m = 10;
        int n = 3;
        int w[]={3,4,5};
        int p[]={4,5,6};
        Pack01 pack = new Pack01();
        int c[][] = pack.pack(m, n, w, p);
        pack.printPack(c, w, m,n);
    }
}

4、鸡蛋和楼的问题

　　动态规划解决：

dp[i][j]表示对于i层楼并拥有j个鸡蛋时能够判断鸡蛋质量需要的最少次数;

假如我们在第k层扔下一个鸡蛋，则有两种情况，如果鸡蛋没有损坏则问题相当于我们对于i-k层楼拥有j个鸡蛋所需的最少的次数。
如果鸡蛋碎了，则问题相当于对于k层楼拥有j-1个鸡蛋的最小次数。从而可以得到动态规划公式：

dp[i][j] = Min( Max( dp[k][j-1], dp[i-k][j] ) ) + 1,  k ∈ [1. i)

得到状态转移方程：

代码：

public static int resolve(int eggs, int floors) {

        int dp[][] = new int[floors+1][eggs+1];

        for(int i = 1; i <= floors; i++) {
            dp[i][1] = i-1;
        }
        for(int i = 1; i <= eggs; i++) {
            dp[1][i] = 0;
        }
        for(int i = 2; i <= floors; i++) {
            for(int j = 2; j <= eggs; j++) {
                int tmp = Integer.MAX_VALUE;
                for(int k = 1; k < i; k++) {
                    tmp = Math.min(tmp, Math.max(dp[k][j-1], dp[i-k][j]));
                }
                dp[i][j] = tmp + 1;
            }
        }
        return dp[floors][eggs];
    }

５、跳台阶

（1）问题
　　有一座高度是10级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法？
（2）想法

　　1级台阶有1种方法；
　　2级台阶有2种方法；
　　3级台阶有3种方法；
　　4级台阶有5种方法；
　　n级台阶有（（n-1)级台阶和(n-2)级台阶）的和。

5.1 递归方法

　　根据上面的想法很容易就能写出递归方式的代码

public int JumpFloor(int target) {
        if(target<1)
            return 0;
        if(target==1)
            return 1;
        if(target==2)
            return 2;
        return JumpFloor(target-1)+JumpFloor(target-2);
    }

但是会发现时间和空间复杂度高，能不能进行简化呐？

5.2 递归简化

　　要计算F(N)，需要计算F(N-1)和F(N-2)的值。依次类推，可以归纳成下面的图：

　　可以发现其中的有些相同的参数被重复计算了，如图相同的颜色被重复计算了：

　　我们可以通过创建一个哈希表，将不同参数的计算结果保存到哈希表中。

public int JumpFloor(int target,HashMap map) {
        if(target<1)
            return 0;
        if(target==1)
            return 1;
        if(target==2)
            return 2;
        if(map.contains(target)){
            return map.get(target);
        }else{
           int value = JumpFloor(target-1)+JumpFloor(target-2);
           map.put(target,value);
           return value;
        }   
    }

　　空间复杂度和时间复杂度都为o(N)。

5.3 动态规划

　　d(i)表示有i个台阶时的总共跳法。
　　可以得到状态转移方程：

　　动态规划是从上到下分析问题，从下到上解决问题。

　　代码：

public int jumpfloor(int target){
        if(target<1)
            return 0;
        if(target==1)
            return 1;
        if(target==2)
            return 2;
        int a = 1;
        int b = 2;
        int temp = 0;
        for(int i = 3; i <= target; i++){
            tem = a + b;
            a = b;
            b = temp;
        }
        return temp;
}

　　空间复杂度为o(1)和时间复杂度为o(N)。

６、国王和金矿

（1）问题
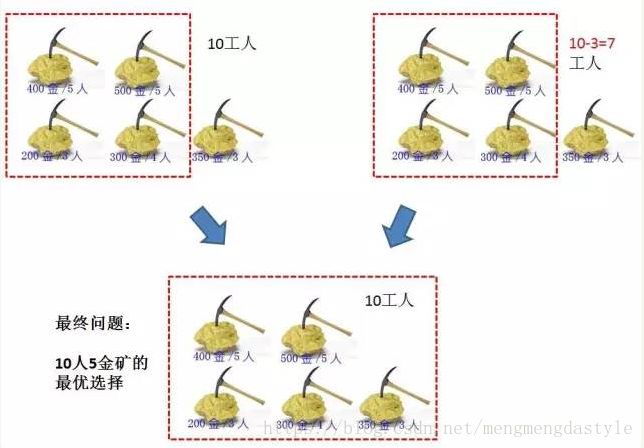
　　有一个国家发现了5座金矿，每座金矿的黄金储量不同，需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖，要么不挖，不能派出一半人挖取一半金矿。要求用程序求解出，要想得到尽可能多的黄金，应该选择挖取哪几座金矿？

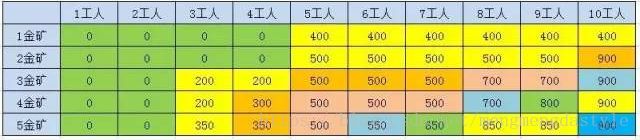
　　5个矿的最优选择，就是（前4座金矿10个工人的挖金数量）和（前4座金矿7工人的挖金数量+第5座金矿的挖金数量）的最大值。
　
（2）动态规划
　　N表示金矿数量，W表示工人数，设金矿的黄金量为G[]，金矿的用工量设为数组P[]。
　　得到状态转移方程：

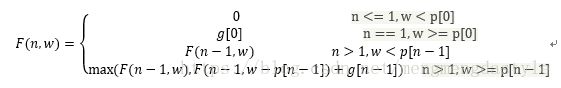
public int getMostGold(int n, int w, int[] g, int[] p){
        int[] preResults = new int[p.length];
        int[] results = new int[p.length];

        //填充边界格子的值
        for(int i = 0; i <= n; i++){
            if(i < p[0]){
                preResults[i] = 0;
            }else{
                preResults[i] = g[0];
            }
        }
        //填充其余格子的值，外层循环是金矿数量，内层循环是工人数
        for(int i = 0;i < n; i++){
            for(int j = 0; j <= w; j++){
                if(j < p[i]){
                    results[j] = preResults[j];
                }else{
                    //实际上就是管不管最后一个金矿的问题
                    results[j] = Math.max(preResults[j],preResults[j-p[i]] + g[i]);                                        
                }
            }
            preResults = results;
        }
        return results[n];        
    }

时间复杂度是 O(n * w)，空间复杂度是(w)。