路径优化搜素算法

一.深度优先搜索算法(DFS)

1.算法介绍

https://zh.wikipedia.org/wiki/深度优先搜索

DFS（Depth-First-Search）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。属于盲目搜索。
一般使用栈(占内存)的数据结构实现。

2.算法步骤

1.访问顶点v
2.依次从v的未被访问的邻接点出发，对图进行深度优先遍历；直至图中和v有路径相通的顶点都被访问
3.若此时图中尚有顶点未被访问，则从一个未被访问的顶点出发，重新进行深度优先遍历，直到图中所有顶点均被访问过为止。

3.举例

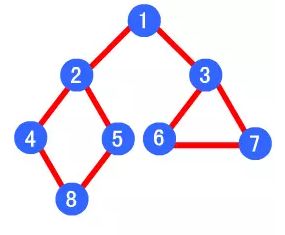
DFS 在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1；再从 w1 出发，访问与 w1邻 接但还没有访问过的顶点 w2；然后再从 w2 出发，进行类似的访问，… 如此进行下去，直至到达所有的邻接顶点都被访问过的顶点 u 为止。
接着，退回一步，退到前一次刚访问过的顶点，看是否还有其它没有被访问的邻接顶点。如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问；如果没有，就再退回一步进行搜索。重复上述过程，直到连通图中所有顶点都被访问过为止。

深度优先遍历顺序为 1->2->4->8->5->3->6->7

二.广度优先搜索(BFS)

1.算法介绍

BFS（Breadth-First-Search）是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。BFS同样属于盲目搜索。
一般使用队列数据结构来实现BFS。

2.步骤

1.首先将根节点放入队列中。
2.从队列中取出第一个节点，并检验它是否为目标。如果找到目标，则结束搜寻并回传结果。否则将它所有尚未检验过的直接子节点加入队列中。
3.若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
4.重复步骤2。

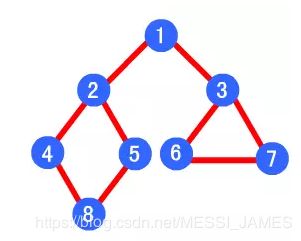
3.举例

广度优先算法的遍历顺序为：1->2->3->4->5->6->7->8

三. Dijkstra算法

1.算法介绍

Dijkstra(迪杰斯特拉)算法使用了广度优先搜索解决赋权有向图的单源最短路径问题。该算法存在很多变体；Dijkstra的原始版本找到两个顶点之间的最短路径，但是更常见的变体固定了一个顶点作为源节点然后找到该顶点到图中所有其它节点的最短路径，产生一个最短路径树。 Dijkstra是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。注意该算法要求图中不存在负权边。

2.步骤

（1）定义变量：
定义一个数组dist，dist[m]表示顶点s到顶点m的最短距离。（在迭代过程中，里面的值可能不是最终最短距离，但是是当前考虑到已经扫描到的边的最短距离）
定义一个集合T，里面存放着已经查询到最终最短路径的顶点集合。
（2）初始化：
任取顶点 i，如果 s 和 i 直接相连，则dist[i]=W(s,i)，否则 W(s, i) 为无穷大。
T 集合只包含顶点 s。
（3）迭代：
A、从dist中找到最小值（除去集合 T 中包含的点），记为 dist[r]=d，然后将顶点 r 划入到集合 T 中。
B、对于每一个不属于集合 T 的点，比如顶点 q， 查看新加入的顶点 r 是否可以直接到达顶点 q，如果是，则比较通过顶点 r 到达顶点 q 的路径长度和当前的dist[q]值，然后取较小值，即 dist[q] := min(dist[r]+W(r, q), dist[q])
C、跳回到步骤A，直到所有的点都进入到了集合 T。
D、dist 中存放的值即为每个点的最终最短路径。

3.举例

https://blog.csdn.net/yalishadaa/article/details/55827681
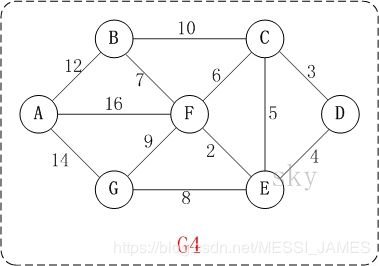
问题描述：在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

初始状态：S是已计算出最短路径的顶点集合，U是未计算除最短路径的顶点的集合！
第1步：将顶点D加入到S中。
此时，S={D(0)}, U={A(∞),B(∞),C(3),E(4),F(∞),G(∞)}。 注:C(3)表示C到起点D的距离是3。

第2步：将顶点C加入到S中。
上一步操作之后，U中顶点C到起点D的距离最短；因此，将C加入到S中，同时更新U中顶点的距离。以顶点F为例，之前F到D的距离为∞；但是将C加入到S之后，F到D的距离为9=(F,C)+(C,D)。
此时，S={D(0),C(3)}, U={A(∞),B(23),E(4),F(9),G(∞)}。

第3步：将顶点E加入到S中。
上一步操作之后，U中顶点E到起点D的距离最短；因此，将E加入到S中，同时更新U中顶点的距离。还是以顶点F为例，之前F到D的距离为9；但是将E加入到S之后，F到D的距离为6=(F,E)+(E,D)。
此时，S={D(0),C(3),E(4)}, U={A(∞),B(23),F(6),G(12)}。

第4步：将顶点F加入到S中。
此时，S={D(0),C(3),E(4),F(6)}, U={A(22),B(13),G(12)}。

第5步：将顶点G加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12)}, U={A(22),B(13)}。

第6步：将顶点B加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13)}, U={A(22)}。

第7步：将顶点A加入到S中。
此时，S={D(0),C(3),E(4),F(6),G(12),B(13),A(22)}。

此时，起点D到各个顶点的最短距离就计算出来了：A(22) B(13) C(3) D(0) E(4) F(6) G(12)。

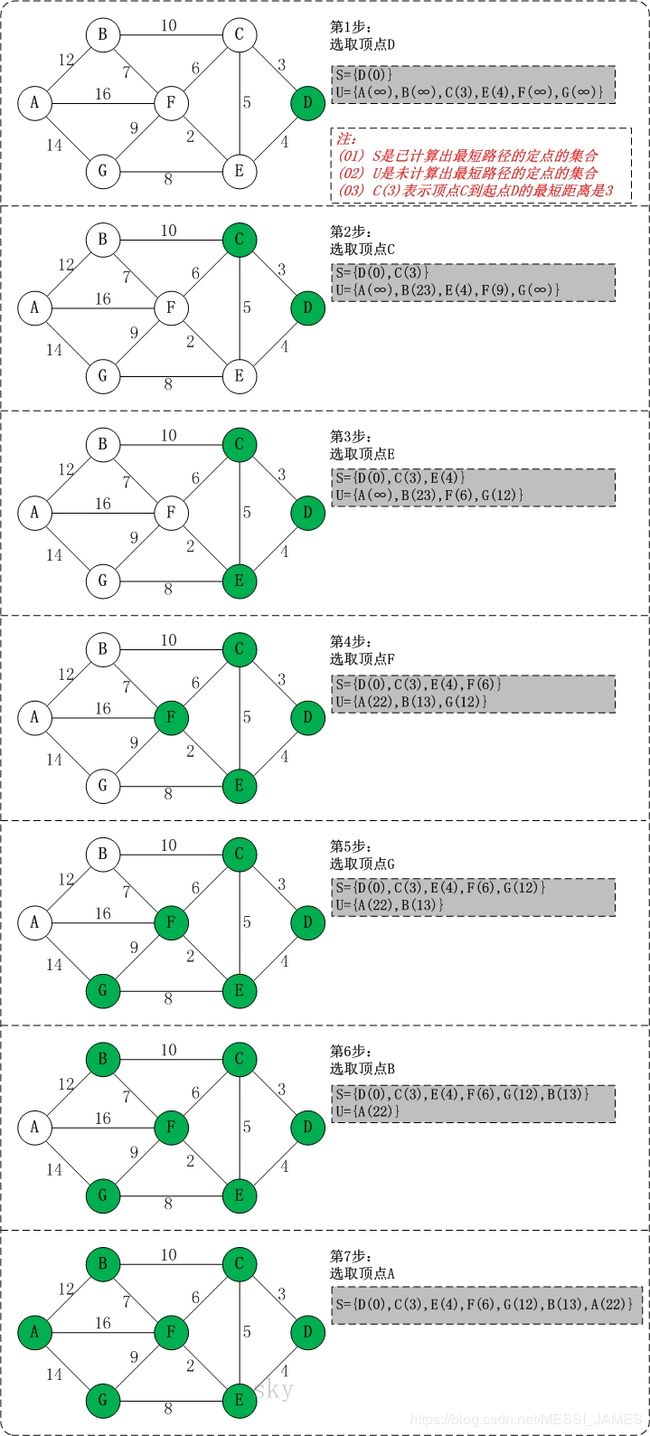
https://blog.csdn.net/qq_35644234/article/details/60870719 帮助理解

四.A*算法

http://forster.site/2018-04-12-A*算法.html

1.算法介绍

A搜寻算法，俗称A星算法，作为启发式搜索算法中的一种，这是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。该算法像Dijkstra算法一样，可以找到一条最短路径；也像BFS一样，进行启发式的搜索。A算法常用于游戏的npc移动计算，不过其不足很明显，有可能需要试探完整个解集空间才能找到较优解。
缺点:A算法很可能需要遍历所有节点才能找到路径，如果在一个大地图中，需要非常耗时。在小范围里，我们可以通过随机，或者设定小目标来使用A算法，提高效率。

2.步骤

A算法最核心就是下面这个公式：f(n)=g(n)+h(n)
f(n)：每个可能试探点的估值
g(n)：从起始搜索点到当前结点的代价
h(n)：当前结点到目标结点的估值
…
h(n)设计的好坏，直接影响着具有此种启发式函数的启发式算法的是否能称为A算法。

假设我们需要把 A 点移动到 B 点，但是这两点之间被一堵墙隔开。 A点到B点过程中，没走一步，准备走下一步时，都有一个状态：可走和不可走。 在开始前，我们需要准备一个集合(closed set) 专门存已经被估算的节点(有点像我们去商场的购物车)；一个集合(open set) 存放将要被估算的节点。还需要一个列表用于记录每个节点的f值。 这里我们的h(n) 使用直接距离来表示节点到目标节点的估值；g(n) 使用该节点沿着父节点(n-1)的g(n-1)累加得到。

开始寻路：
1.首先起点 A 开始，并把它就加入到 open set中。
2.查看与起点 A 相邻的节点，把其中可走的节点也加入到 open set。把起点 A 设置为这些节点的父节点 。
3.open set 移除A，A加入 closed set。
4.在open set选一个 f(n) 最小的节点，放到closed set。
5.检查这个最小的节点附近所有可走的点，把可走的点放入open set。
6.如果可走的点已经在open set，则检查这个点作为父节点的g(n) 是否比之前在open set时的小，如果比之前小，则替换成新的父节点。
7.不断重复上面的过程，直到目标节点在closed set中，或者open set 为空。
8.目标节点沿着父节点递归，直到找到A，那么此时找到完整的路径。

3.代码实现(python)

# -*- coding: utf-8 -*-
import common.conf as conf
# A*算法结构体
class A_star:
    def __init__(self, s_x, s_y, e_x, e_y):
        self.s_x = s_x
        self.s_y = s_y
        self.e_x = e_x
        self.e_y = e_y
        self.opened = {}
        self.closed = set()
        self.path = []
        self.dead = set()
    # 寻路
    def cal_path(self):
        p = Node(None, self.s_x, self.s_y, 0.0)
        self.opened[p.id] = p
        # 遍历open集合，直到open集合为空
        while len(self.opened) > 0:
            # 获取最优f值对应的node
            idx, node = self.get_best()
            # 如果node是终点，则输出路径
            if node.x == self.e_x and node.y == self.e_y:
                self.make_path(node)
                return
            # 把最优f值放到close集合，open集合去掉这个node
            self.closed.add(node.id)
            del self.opened[node.id]
            # 获取node附近的点
            self.get_neighboor(node)
    # 输出到终点的路径
    def make_path(self, p):
        while p:
            self.path.append((p.x, p.y))
            p = p.parent
        self.path.reverse()
        # 把start点去掉
        if len(self.path) > 1:
            del self.path[0]
    # 遍历opened集合获取最优f值的node
    def get_best(self):
        best = None
        f_cost = 10000000000
        bi = None
        for key, item in self.opened.iteritems():
            value = self.get_f(item)
            if value < f_cost:
                best = item
                f_cost = value
                bi = key
        return bi, best
    # 获取f值
    def get_f(self, i):
        return i.g_cost + (self.e_x - i.x)**2 + (self.e_y - i.y)**2
    # 获取p附近的node
    def get_neighboor(self, p):
        # 四个方向
        xs = (0, -1, 1, 0)
        ys = (-1, 0, 0, 1)
        for x, y in zip(xs, ys):
            new_x, new_y = x + p.x, y + p.y
            # 判断node是否可到达
            if self.is_valid(new_x, new_y) is False:
                continue
            # 新建node对象
            node = Node(p, new_x, new_y, p.g_cost+self.get_cost(p.x, p.y, new_x, new_y))
            if node.id in self.closed:
                continue
            # node在open集合
            if node.id in self.opened:
                # open集合的g值比目前的node的g值大，则open集合中node的g值为该node的g值
                if self.opened[node.id].g_cost > node.g_cost:
                    self.opened[node.id].parent = p
                    self.opened[node.id].g_cost = node.g_cost
                    # self.f_cost[node.id] = self.get_f(node)
                else:
                    # node不在open集合中，加入open集合
                    self.opened[node.id] = node
    # 判断node是否可到达
    def is_valid(self, x, y):
        if abs(x) > 150 or y < -80 or y > 300:
            return False
        tmp_str = str(x) + '|' + str(y)
        # 已经在废弃集合中
        if tmp_str in self.dead:
            return False
        # 遍历墙
        for index, value in enumerate(conf.WALLS[1]):
            if abs(x - value[0]) <= 25 and abs(y - value[1]+25) <= 5:
                self.dead.add(tmp_str)
                return False
        return True
    # 获取g值
    def get_cost(self, x1, y1, x2, y2):
        if x1 == x2 or y1 == y2:
            return 1.0
        return 1.4
# 点的结构
class Node(object):
    def __init__(self, parent, x, y, g_cost):
        self.parent = parent
        self.x = x
        self.y = y
        self.id = str(x) + '|' + str(y)
        self.g_cost = g_cost

加强理解
https://blog.csdn.net/v_JULY_v/article/details/6093380
https://zhuanlan.zhihu.com/p/39094428
https://www.jianshu.com/p/8905d4927d5f
https://www.cnblogs.com/warnet/p/6838044.html

A*算法总结

1. 把起点加入 open list 。
2. 重复如下过程：
   a. 遍历 open list ，查找 F 值最小的节点，把它作为当前要处理的节点。
   b. 把这个节点移到 close list 。
   c. 对当前方格的 8 个相邻方格的每一个方格？
   ◆ 如果它是不可抵达的或者它在 close list 中，忽略它。否则，做如下操作。
   ◆ 如果它不在 open list 中，把它加入 open list ，并且把当前方格设置为它的父亲，记录该方格的 F ， G 和 H 值。
   ◆ 如果它已经在 open list 中，检查这条路径 ( 即经由当前方格到达它那里 ) 是否更好，用 G 值作参考。更小的 G 值表示这是更好的路径。如果是这样，把它的父亲设置为当前方格，并重新计算它的 G 和 F 值。如果你的 open list 是按 F 值排序的话，改变后你可能需要重新排序。
   d. 停止，当你
   ◆ 把终点加入到了 open list 中，此时路径已经找到了，或者
   ◆ 查找终点失败，并且 open list 是空的，此时没有路径。
3. 保存路径。从终点开始，每个方格沿着父节点移动直至起点，这就是你的路径。

五.Dijkstra算法和A*算法对比

1.Dijkstra算法计算源点到其他所有点的最短路径长度，A关注点到点的最短路径(包括具体路径)。
2.Dijkstra算法建立在较为抽象的图论层面，A算法可以更轻松地用在诸如游戏地图寻路中。
3.Dijkstra算法的实质是广度优先搜索，是一种发散式的搜索，所以空间复杂度和时间复杂度都比较高。对路径上的当前点，A算法不但记录其到源点的代价，还计算当前点到目标点的期望代价，是一种启发式算法，也可以认为是一种深度优先的算法。
4.由第一点，当目标点很多时，A算法会带入大量重复数据和复杂的估价函数，所以如果不要求获得具体路径而只比较路径长度时，Dijkstra算法会成为更好的选择

A*算法加入了启发函数，用于引导其搜索方向，所以大部分情况下A*算法会比Dijkstra算法规划速度快不少。

六.Dijkstra和A*算法演示

https://www.jiqizhixin.com/articles/2019-08-03-3