【数据结构与算法分析】二叉查找树与AVL树

二叉树与普通树的区别在于二叉树的每个节点最多只能有两个儿子，节点就是有所存储的元素信息加上对其他节点（左、右子树）的引用组成的结构。表达式树就是二叉树一个很好地实现，如下图

表达式树可以由后序表达式转化而来，下图就实现了这个想法

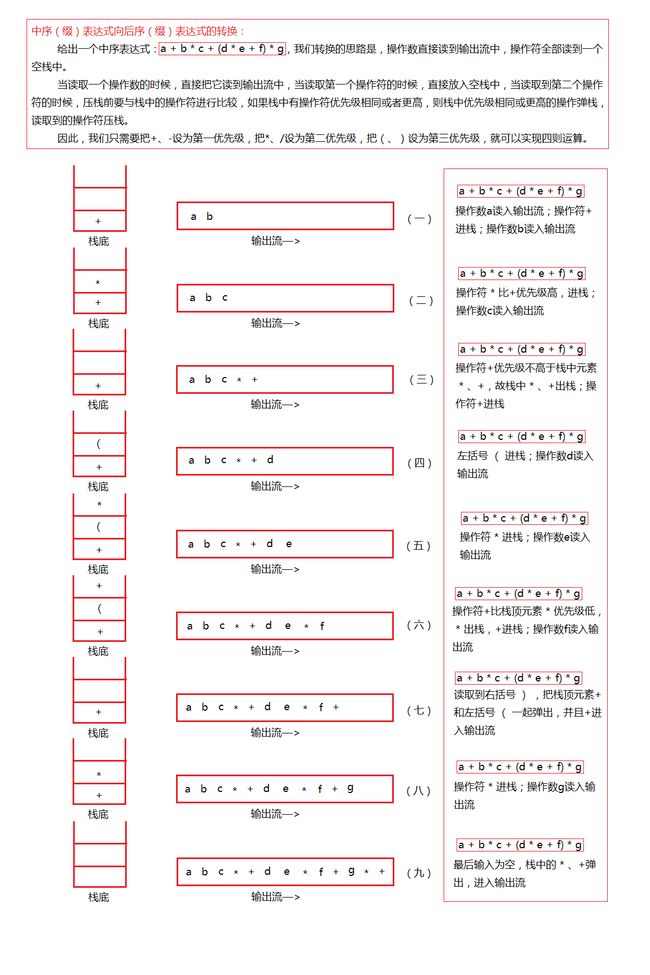
而后序表达式又可以通过中序表达式转化而来，据悉转化过程见下图

查找树ADT——二叉查找树的实现细节

使二叉树成为二叉查找树的性质是，对于树中的每个节点X，它的左子树中所有项的值小于X中项的值，而它的右子树中所有项的值大于X中的项。下面的代码是二叉查找树节点类实现，代码如下

/*
 *
 *
 *BinaryNode:二叉查找树的节点类
 *
 *
 **/
private static class BinaryNode {

    AnyType element;
    BinaryNode left;
    BinaryNode right;

    // 构造器
    BinaryNode (AnyType theElement) {
        this (theElement, null, null);
    }

    BinaryNode(AnyType theElement, BinaryNode lt, 
                                BinaryNode rt) {
        element = theElement;
        left = lt;
        right = rt;
    }
}

/*
 *
 *
 *二叉查找树架构
 *
 *
 **/
public class BinarySearchTree> {

    private static class BinaryNode {
        ...
    }

    private BinaryNode root;

    public BinarySearchTree() {
        root = null;
    }

    public void makeEmpty() {
        root = null;
    }

    public boolean isEmpty() {
        return root == null;
    }

    public boolean contains (AnyType x) {
        return contains(x, root);
    }

    private AnyType findMin() {
        if (isEmpty()) 
            throw new UnderflowException();
        return findMin(root).element;
    }

    public AnyType findMax() {
        if (isEmpty()) throw new UnderflowException();
        return findMax(root).element;
    }

    public void insert(AnyType x) {
        root = insert(x, root);
    }

    public void remove(AnyType x) {
        root = remove(x, root);
    }

    public void printTree() {
        ...
    }

    private boolean contains(AnyType x, BinaryNode t) {
        ...
    }

    private BinaryNode findMin(BinaryNode t) {
        ...
    }

    private BinaryNode findMax(BinaryNode t) {
        ...
    }

    private BinaryNode insert(AnyType x, BinaryNode t) {
        ...
    }

    private BinaryNode remove(AnyType x, BinaryNode t) {
        ...
    }

    private void printTree(BinaryNode t) {
        ...
    }
}

从上面我们也能看出二叉查找树提供了insert()、remove()、findMin()、findMax()、contains()、printTree()等方法我们接下来看看二叉查找树为的这些功能是怎样实现的。

/*
 *
 *
 * contains()方法实现
 *
 *
 **/
private boolean contains(AnyType x, BinaryNode t) {

    if (t == null ) {
        return false;
    }

    int compareResult = x.compareTo(t.element);
    if (compareResult < 0) {
        return contains(x, t.left);
    } else if (compareResult > 0) {
        return contains(x, t.right);
    } else {
        return true;    //Match
    }

} 

/*
 *
 *
 * findMin() 和findMax()方法实现
 *
 *
 **/
 private BinaryNode findMin(BinaryNode t) {
    if (t == null) {
        return null;
    } else if (t.left == null) {
        return t;
    } 
    return findMin(t.left);
 }

 private BinaryNode findMax(BinaryNode t) {
    if (t != null) {
        while (t.right != null) {
            t = t.right;
        }
    }
    return t;
 }

/*
 *
 *
 * insert()方法实现
 *
 *
 **/
 private BinaryNode insert(AnyType x, BinaryNode t) {

    if (t == null) {
        return new BinaryNode(x, null, null);
    }
    int compareResult = x.compareTo(t.element);
    if (compareResult <0) {
        t.left = insert(x, t.left);
    } else if (compareResult > 0) {
        t.right = insert(x, t.right);
    } else {
        ; //Duplicate, do nothing
    }
    return t;
 }

/*
 *
 *
 * remove()方法实现
 *
 *
 **/
 private BinaryNode remove(AnyType x, BinaryNode t) {

    if (t == null) {
        return t;   //item not found, do nothing
    }
    int compareResult = x.compareTo(t.element);
    if (compareResult < 0) {
        t.left = remove(x, t.left);
    } else if (compareResult > 0) {
        t.right = remove(x, t.right);
    } else if (t.left != null && t.right != null) {
        t.element = findMin(t.right).element;
        t.right = remove(t.element, t.right);
    } else {
        t = (t.left != null) ? t.left : t.right;
    }
    return t;

 }