【语义分割】Auto-DeepLab Hierarchical Neural Architecture Search for Semantic Image Segmentation阅读翻译
论文地址:https://arxiv.org/abs/1901.02985 1月10号提交
代码:2019.05.03更新,找到一份非官方的Pytorch实现代码 https://github.com/MenghaoGuo/AutoDeeplab
作者:Chenxi Liu, Liang-Chieh Chen, Florian Schroff, Hartwig Adam, Wei Hua, Alan Yuille, Li Fei-Fei
参考资料:李飞飞等人提出Auto-DeepLab:自动搜索图像语义分割架构-机器之心
目录
- 摘要
- 1.介绍
- 2.相关工作
- 3.架构搜索空间
- 3.1单元级搜索空间
- 3.2网络级搜索空间
- 4.方法
- 4.1连续松弛的架构
- 4.1.1单元架构
- 4.1.2网络架构
- 4.2优化
- 4.3解码离散架构
- 5.实验结果
- 5.1架构搜索实现细节
- 5.2语义分割结果
- 5.2.1Cityscapes
- 5.2.2 PASCAL VOC 2012
- 5.2.3 ADE20K
- 6.结论
摘要
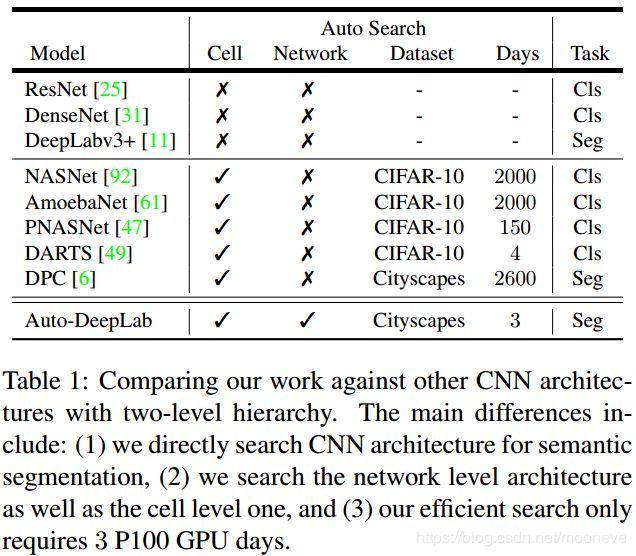
近期,在大规模图像分类问题上神经架构搜索(Neural Architecture Search,NAS)确定的神经网络框架的表现超越了人类设计的网络。本论文将研究用于图像语义分割的 NAS,图像语义分割是将语义标签分配给图像中每个像素的重要计算机视觉任务。现有的研究通常注重搜索可重复的单元结构,而对控制空间分辨率变化的外部网络结构进行人工设计。这种做法简化了搜索空间,但对于具备大量网络级架构变体的密集图像预测而言,该方法越来越成问题。因此,我们建议除了搜索单元级结构之外还要搜索网络级架构,从而形成分层架构搜索空间。我们提出包含许多流行网络设计的网络级搜索空间,并提出一个公式来进行基于梯度的高效架构搜索(Cityscapes 图像上使用P100 GPU需要3天)。我们证明了所提方法在具有挑战性的Cityscapes,PASCAL VOC 2012和ADE20K数据集上的有效性。在不经任何 ImageNet 预训练的情况下,我们搜索得到的专用于语义图像分割的架构获得了当前最优性能。
1.介绍
深度神经网络已被证明在各种人工智能任务中都是成功的,包括图像识别[38,25],语音识别[27],机器翻译[72,80]等。虽然更好的优化[36]和更好的归一化技术[32,79]在其中发挥了重要作用,但很多进展都来自神经网络架构的设计。在计算机视觉中,这适用于图像分类[38,71,74,75,73,25,84,31,30]和密集图像预测[16,51,7,63,56,55]。
最近,本着AutoML和AI民主化的精神,人们对自动设计神经网络架构非常感兴趣,而不是非常依赖专家经验和知识。重要的是,过去的一年中,神经架构搜索(NAS)在大规模图像分类问题[92,47,61]上已成功提出超出人类设计架构的网络框架。
图像分类(Image classification)是NAS一个很好的起点,因为它是最基础和研究最充分的高级识别任务。同时,该研究领域存在具有规模相对较小的基准数据集(如 CIFAR-10),这减少了计算量并加快了训练速度。然而,图像分类不应该成为NAS的终点,当前的成功表明它可以扩展至要求更高的领域。在本文,我们研究了将神经架构搜索用于图像语义分割的方法,图像语义分割是计算机视觉中的重要任务,它将诸如“person”或“bicycle”等标签分配给输入图像的每个像素。
简单地将图像分类中ideas移植不足以进行语义分割。在图像分类中,NAS通常使用从低分辨率图像到高分辨率图像的迁移学习[92],而语义分割的最佳框架必须固有地在高分辨率图像上运行。这提示我们需要:(1)一个更宽松和通用的搜索空间,用于捕捉更高分辨率带来的架构变化,和(2)一个更高效的架构搜索技术,因为更高的分辨率需要更多的计算。
我们注意到现代CNN设计[25,84,31]通常遵循两级分层结构(two-level hierarchy),其中外部网络级控制空间分辨率变化,内部单元级控制特定的分层计算。当前NAS [92,47,61,59,49]的绝大部分工作遵循这种两级分层设计,但只在内部单元级别使用自动搜索,而外部网络级别使用手动设计。这种有限的搜索空间对于密集图像预测而言是一个问题,因为密集图像预测对空间分辨率变化很敏感。因此在我们的工作中,我们提出了类似网格的网络级搜索空间,它增强了[92]中首次提出的常用单元级搜索空间,从而形成分层架构搜索空间。我们的目标是联合学习到专门用于图像语义分割的可重复的单元结构与网络结构的良好组合。
就架构搜索方法而言,强化学习[91,92]和进化算法[62,61]即使在低分辨率CIFAR-10数据集上也往往是计算密集型的,因此可能不适合图像语义分割。我们从NAS的可微分公式[68,49]中汲取灵感,并开发出与分层架构搜索空间完全匹配的连续松弛的离散架构。分层架构搜索通过随机梯度下降进行。当搜索终止时,最好的单元架构会被贪婪解码,最好的网络架构会有效的通过Viterbi算法解码。我们直接在裁剪得到的Cityscapes[13] 321×321图像上进行架构搜索。该搜索十分有效,在单个P100 GPU上只需要花费3天时间。
连续松弛的离散架构没看懂,下面仔细琢磨琢磨。
我们报告了多个语义分割基准的实验结果,包括Cityscapes [13],PASCAL VOC 2012 [15]和ADE20K [89]。在未经ImageNet[64]预训练的情况下,我们的最佳模型在Cityscapes测试集上的性能超过FRRN-B [60] 8.6%,超过GridNet [17] 10.9%。当利用Cityscapes粗略标注数据时,我们的模型与其他经过ImageNet预训练的最先进模型[81,87,4,11,6]表现相当。值得注意的是,我们的最佳模型(没有预训练)获得与DeepLabv3 + [11](有预训练)相同的性能,但在Multi-Adds中的速度提高2.23倍。此外,我们的轻量级模型的性能仅比DeepLabv3 +低11%[11],但参数减少了76.7%,在Multi-Adds中的速度提高了4.65倍。最后,在PASCAL VOC 2012和ADE20K上,我们的最优模型在使用极少数据进行预训练的情况下,性能优于几个当前最先进模型[89,44,81,87,82]。
总而言之,我们论文的贡献有四个方面:
- 我们是首次将NAS从图像分类扩展到密集图像预测的尝试之一。
本文第二作者去年9月份发表了一篇也是用NAS做语义分割,即本文中的参考文献6,代码就放在Deeplab中 罒ω罒,详见我另外一篇文章:https://blog.csdn.net/mooneve/article/details/83144385 (这篇内容我都忘差不多了-_-||,正好回去再看一次,只记得性能和DeeplabV3+相似,但参数数量和训练时间少了很多。)
- 我们提出了一个网络级架构搜索空间,它可以增强和补充已经得到深入研究的单元级架构搜索,并对网络级和单元级架构进行更具挑战性的联合搜索。
- 我们开发出一个可微的连续公式,它可以在两级分层架构上进行有效搜索,在单个GPU上只需3天。
- 在Cityscapes上,未经ImageNet预训练的情况下,我们的模型显著优于FRRN-B和GridNet,经过ImageNet预训练的情况下,我们和其他最先进模型的表现相当。在PASCAL VOC 2012 和ADE20K上,我们最好的模型也优于几个当前最先进的模型。
2.相关工作
图像语义分割 以全卷积方式应用的卷积神经网络[42](FCN [67,51])在几个语义分割基准上取得了显着的成绩。在最先进的系统中,有两个重要组件:多尺度上下文模块和神经网络设计。众所周知,上下文信息对像素标记任务至关重要[26,69,37,39,16,54,14,10]。因此,PSPNet [87]在几个网格尺度上应用空间金字塔池化[21,41,24](包括图像级池化[50]),而DeepLab [8,9]应用几个并行的有不同孔洞率的孔洞卷积[28,20,67,57,7]。另一方面,神经网络设计的改进极大地将性能从AlexNet [38],VGG [71],Inception [32,75,73],ResNet [25],推动到更新的架构,如Wide ResNet [ 85],ResNeXt [84],DenseNet [31]和Xception [12]。除了采用这些网络作为语义分割的主干网络之外,还可以采用编码器 - 解码器结构[63,2,55,44,60,58,33,78,18,11,86,82],它们在保持对象详细边界的同时有效地捕获了长距离的上下文信息。然而,对于语义分割任务,大多数模型需要从经过ImageNet [64]预训练的checkpoint开始进行初始化,除了FRRN [60]和GridNet [17]。具体来说,FRRN [60]采用双流系统,其中一个流携带全分辨率信息,另一个流池携带上下文信息。GridNet建立在类似的想法之上,它包含多个具有不同分辨率的流。在本文工作中,我们使用神经架构搜索找到特定于语义分割的网络骨干。我们进一步展示了没有经过ImageNet预训练的最先进的性能,并且在Cityscapes[13]上显著优于FRRN [60]和GridNet [17]。
神经架构搜索方法 神经架构搜索旨在自动设计神经网络架构,从而最大限度地减少人工时间和工作量。虽然有些工作[22,34,91,49]搜索RNN单元用于语言任务,但更多工作搜索良好的CNN架构进行图像分类。
一些论文使用强化学习(reinforcement learning)(policy gradients[91,92,5,66]或Q-learning[3,88])来训练递归神经网络,该神经网络表示一个策略,该策略用于生成一个符号序列,其中符号指定特定的CNN架构。RL的替代方案是使用进化算法(evolutionary algorithms,EA),通过改变迄今为止发现的最佳架构来“进化”架构[62,83,53,48,61]。然而,这些RL和EA方法在搜索过程中往往需要大量计算,通常需要单个GPU运行几千天。PNAS [47]提出了一种渐进式搜索策略,该策略显著降低了搜索成本,同时保持了搜索架构的质量。NAO [52]将架构嵌入到潜在空间中并在解码之前执行优化。此外,一些工作[59,49,1]利用了采样模型之间的架构共享,而不是单独训练它们中的每一个,从而进一步降低了搜索成本。我们的工作遵循可微分的NAS公式[68,49],并将其扩展到更一般的分层设置中。
神经架构搜索空间 早期论文,如[91,62],试图直接构建整个网络。然而,最近更多的论文[92,47,61,59,49]已转向搜索可重复的单元结构,同时保持外部网络级结构手动固定。这种策略在[92]中首次提出,很可能是受到现代CNN中常用的两级分层结构的启发。
我们的工作仍然使用此单元级搜索空间,从而与以前的工作保持一致。然而,我们的一个贡献是提出一个新的通用网络级搜索空间,因为我们希望联合搜索这个两级分层结构。我们的网络级搜索空间与[66]相似,但重要的区别在于[66]保持整个“结构”无意改变架构,而我们将每个连接的权重显式关联起来并专注于解码单个分离的结构。同时,[66]是对人脸图像分为3类[35]进行评估,而我们的模型则在大规模数据集上进行评估,如Cityscapes [13],PASCAL VOC 2012 [15]和ADE20K [89]。
与我们最相似的工作是[6],它也研究NAS用于图像语义分割。然而,[6]专注于使用随机搜索方法搜索更小的孔洞空间金字塔池(Atrous Spatial Pyramid Pooling,ASPP)模块,而我们专注于使用更先进和更有效的搜索方法搜索更基本的网络骨干架构。
3.架构搜索空间
本节介绍我们的两级分层结构搜索空间。 对于内部单元级(第3.1节),我们复用[92,47,61,49]中采用的方法,从而与以前的工作保持一致。对于外部网络级(第3.2节),我们基于对许多流行设计的观察和总结提出了一种新颖的搜索空间。
3.1单元级搜索空间
我们将一个小的全卷积模块定义为一个单元(cell),通常它会在整个神经网络中重复很多次。更具体地说,一个单元是由 B B B个块(block)组成的有向无环图。
每个块是双分支结构,将两个输入张量(tensor)映射到一个输出张量。单元 l l l 中的块 i i i 通常用一个5元组表示 ( I 1 , I 2 , O 1 , O 2 , C ) (I_1, I_2, O_1, O_2, C) (I1,I2,O1,O2,C),其中 I 1 , I 2 ∈ I i l I_1,I_2\in I^l_i I1,I2∈Iil是输入张量的选择, O 1 , O 2 ∈ O O_1, O_2\in O O1,O2∈O是输入张量的层类型的选择, C ∈ C C \in C C∈C是用于组合两个分支输出的方法,用于形成该块的输出张量 H i l H^l_i Hil。单元的输出张量 H l H^l Hl是所有块输出张量 { H 1 l , . . . , H B l } \{H^l_1,...,H^l_B\} {H1l,...,HBl}的简单级联。
可能的输入张量 I i l I^l_i Iil的集合由前一个单元的输出 H l − 1 H^{l-1} Hl−1,再前一个单元的输出 H l − 2 H^{l-2} Hl−2,和当前 { H 1 l , . . . , H i l } \{H^l_1,...,H^l_i\} {H1l,...,Hil}单元中前面块的输出组成。因此,当我们往单元加入的块越多,那么下一个块的潜在输入源就会有更多的选择。
可能的层类型 O O O的集合由以下8个操作(operator)组成,这些操作在现代CNN中都很普遍:
- 3 × 3的深度分离卷积
- 5 × 5的深度分离卷积
- 3 × 3的孔洞卷积 ,孔洞率为2
- 5 × 5的孔洞卷积 ,孔洞率为2
- 3 × 3的平均池化
- 3 × 3的最大池化
- 跳跃连接(skip connection)
- 无连接(no connection(zero))
对于可能的组合操作(combination operators) C C C的集合,我们只采用简单的对应元素相加这个方法。
3.2网络级搜索空间
在由[92]开创的图像分类NAS框架中,一旦找到单元结构,整个网络就使用预定义的模式构建。因此,网络级不是架构搜索的一部分,因此其搜索空间从未被提出或设计过。
这种预定义的模式简单明了:通过插入“缩小单元”(将空间分辨率除以2并将滤波器数乘以2的单元),将许多“正常单元”(保持特征张量空间分辨率的单元)平等的分隔开。这种下采样策略在图像分类情况下是合理的,但在密集图像预测中,保持高空间分辨率也很重要,因此存在更多的网络级别变化[9,56,55]。
在用于密集图像预测的各种网络架构中,我们注意到两个一致的原则:
- 下一层的空间分辨率要么是两倍大,要么是两倍小,要么保持不变。
- 最小的空间分辨率是下采样32倍。
遵循这些常规做法,我们提出以下网络级搜索空间。网络的开头是一个双层“枝干”(stem)结构,每个枝干都将空间分辨率降低2倍。之后,总共有L层具有未知空间分辨率的单元,分辨率的最大值是被下采样4倍,最小值是被下采样32倍。由于每层空间分辨率可能至多为2倍不同,因此枝干后的第一层只能被下采样4倍或8倍。我们在图1中说明了我们的网络级搜索空间。我们的目标是在这个L层网格中找到一条好的路径。

在图2中,我们展示了我们的搜索空间足以覆盖许多流行的设计。在未来,我们计划进一步放宽这个搜索空间以包括U-net架构[63,45,70],其中层 l l l 除了 l − 1 l-1 l−1之外还可以从 l l l之前的一个层接收输入。
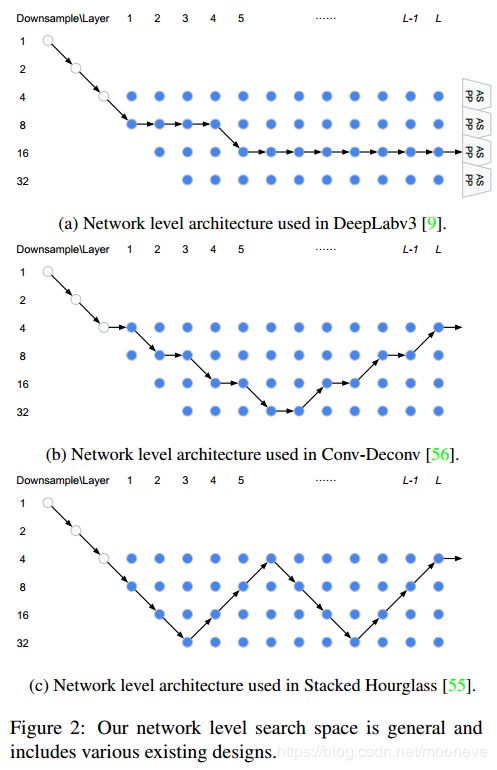
我们重申,除了单元级架构之外,我们的工作还会搜索网络级架构。 因此,我们的搜索空间比以前的作品更具挑战性和通用性。
4.方法
我们首先介绍与上述分层架构搜索完全匹配的连续松弛的(指多数个)离散架构。然后,我们讨论如何进行架构搜索优化,以及如何在搜索终止后解码一个离散架构。
4.1连续松弛的架构
4.1.1单元架构
我们复用了[49]中描述的连续松弛。每一个块的输出 H i l H^l_i Hil会与 I i l I^l_i Iil所有的隐藏状态(4.1.2节有讲隐藏状态的含义)相连:
(1) H i l = ∑ H j l ∈ I i l O j → i ( H j l ) H^l_i=\sum_{H^l_j\in I^l_i} O_{j\to i}(H^l_j) \tag{1} Hil=Hjl∈Iil∑Oj→i(Hjl)(1)
同时,对于每个 O j → i O_{j\to i} Oj→i我们用它的连续松弛来近似它,其定义为:
(2) O ˉ j → i ( H j l ) = ∑ O k ∈ O α j → i k O k ( H j l ) \bar{O}_{j\to i}(H^l_j) =\sum_{O^k \in O}\alpha^k_{j \to i}O^k(H^l_j)\tag{2} Oˉj→i(Hjl)=Ok∈O∑αj→ikOk(Hjl)(2)
其中
(3) ∑ k = 1 ∣ O ∣ α j → i k = 1 ∀ i , j \sum_{k=1}^{|O|}\alpha^k_{j \to i} = 1 \ \ \ \ \ \forall i,j \tag{3} k=1∑∣O∣αj→ik=1 ∀i,j(3)
(4) α j → i k ≥ 0 ∀ i , j , k \alpha^k_{j \to i} \geq 0 \ \ \ \ \ \forall i,j,k \tag{4} αj→ik≥0 ∀i,j,k(4)
换句话说, α j → i k \alpha^k_{j \to i} αj→ik是与每个操作 O k ∈ O O^k \in O Ok∈O相关联的归一化标量,易于用softmax实现。
回忆一下3.1节, H l − 1 H^{l-1} Hl−1和 H l − 2 H^{l-2} Hl−2通常被包含在 I i l I^l_i Iil中, H l H^l Hl是 { H 1 l , . . . , H B l } \{H^l_1,...,H^l_B\} {H1l,...,HBl}的级联。联合公式1和公式2,单元级的更新可以被总结为:
(5) H l = C e l l ( H l − 1 , H l − 2 ; α ) H^l = Cell(H^{l-1}, H^{l-2};\alpha) \tag{5} Hl=Cell(Hl−1,Hl−2;α)(5)
说白了,这一节和3.1节中块i的五元组 ( I 1 , I 2 , O 1 , O 2 , C ) (I_1, I_2, O_1, O_2, C) (I1,I2,O1,O2,C)对应, i , j i,j i,j表示单元中块的索引。在这里 H j l H^l_j Hjl就是 I 1 I_1 I1或 I 2 I_2 I2。 k k k表示该块中分支的索引,取值为1或2,因为只有两个分支┓( ´∀` )┏。
简单表示就是 H i l = α 1 ∗ O 1 ( I 1 ) + α 2 ∗ O 2 ( I 2 ) H^l_i=\alpha^1 *O_1(I_1) + \alpha^2 *O_2(I_2) Hil=α1∗O1(I1)+α2∗O2(I2),这也就是3.1节中说的简单的对应元素相加,所以 α 1 + α 2 = 1 \alpha^1 + \alpha^2 = 1 α1+α2=1。
4.1.2网络架构
在一个单元内,所有张量具有相同的空间分辨率,这使得公式1和公式2可以求(加权)和。然而,如图1清楚所示,张量可以在网络级中采用不同的大小。因此为了建立连续松弛,每层 l l l将至多具有4个隐藏状态 { 4 H l , 8 H l , 16 H l , 32 H l } \{^4H^l, ^8H^l, ^{16}H^l, ^{32}H^l\} {4Hl,8Hl,16Hl,32Hl},左上标表示空间分辨率。
我们设计网络级连续松弛用于准确匹配3.2节描述的搜索空间。我们用一个标量与图1中的每个灰色箭头相关联,然后网络级的更新为:
(6) s H l = β s 2 → s l C e l l ( s 2 H l − 1 , s H l − 2 ; α ) + β s → s l C e l l ( s H l − 1 , s H l − 2 ; α ) + β 2 s → s l C e l l ( 2 s H l − 1 , s H l − 2 ; α ) ^sH^l = \beta^l_{\frac{s}{2} \to s}Cell(^\frac{s}{2}H^{l-1}, ^sH^{l-2};\alpha) \\ + \beta^l_{s\to s}Cell(^sH^{l-1}, ^sH^{l-2};\alpha) \\ + \beta^l_{2s\to s}Cell(^{2s}H^{l-1}, ^sH^{l-2};\alpha) \tag{6} sHl=β2s→slCell(2sHl−1,sHl−2;α)+βs→slCell(sHl−1,sHl−2;α)+β2s→slCell(2sHl−1,sHl−2;α)(6)
其中, s = 4 , 8 , 16 , 32 s=4,8,16,32 s=4,8,16,32 , l = 1 , 2 , . . . , L l=1,2,...,L l=1,2,...,L。标量 β \beta β被归一化以下方式,同样使用softmax实现:
(7) β s 2 → s l + β s → s l + β 2 s → s l = 1 ∀ s , l \beta^l_{\frac{s}{2} \to s} + \beta^l_{s\to s} +\beta^l_{2s\to s}=1 \ \ \ \ \forall s,l \tag{7} β2s→sl+βs→sl+β2s→sl=1 ∀s,l(7)
(8) β s 2 → s l ≥ 0 β s → s l ≥ 0 β 2 s → s l ≥ 0 ∀ s , l \beta^l_{\frac{s}{2} \to s} \geq 0\ \ \beta^l_{s\to s} \geq 0\ \ \beta^l_{2s\to s} \geq 0\ \ \ \ \forall s,l \tag{8} β2s→sl≥0 βs→sl≥0 β2s→sl≥0 ∀s,l(8)
公式6显示了如何将两级分层结构的连续松弛编织在一起。特别地, β \beta β控制外部网络级,因此它取决于空间大小和层索引。 β \beta β中的每个标量控制整组 α \alpha α,但指向与 β \beta β同一架构的 α \alpha α既不依赖于空间大小也不依赖于层索引。
如图1所示,孔洞空间金字塔池化(Atrous Spatial Pyramid Pooling,ASPP)模块被添加到第L层的每个空间分辨率上(相应地调整孔洞率)。它们的输出会双线性上采样到原始分辨率,然后求和以产生预测。
4.2优化
引入这种连续松弛的优点是控制不同隐藏状态之间的连接强度的标量现在是可微分计算图的一部分。因此,它们可以通过梯度下降方法得到有效的优化。我们采用[49]中的一阶近似,并将训练集分为两个不相交的集合trainA和trainB。 优化在以下二者之间交替进行:
- 使用 ∇ w L t r a i n A ( w , α , β ) \nabla_wL_{trainA}(w,\alpha, \beta) ∇wLtrainA(w,α,β)更新网络权重 w w w
- 使用 ∇ α , β L t r a i n B ( w , α , β ) \nabla_{\alpha, \beta}L_{trainB}(w,\alpha, \beta) ∇α,βLtrainB(w,α,β)更新架构标量 α , β \alpha, \beta α,β
其中损失函数 L L L是在语义分割小批量上计算的交叉熵。
4.3解码离散架构
单元架构 与[49]一样,我们首先为每个块保留2个最强的前驱(predecessors)(隐藏状态 j j j到隐藏状态 i i i的强度是 m a x k , O k ≠ z e r o α j → i k max_{k,O^k \neq zero}\alpha^k_{j\to i} maxk,Ok̸=zeroαj→ik,见3.1节“zero”含义是“无连接”),然后通过取argmax来选择最可能的操作(operator)来解码离散单元架构。
强度的定义可见4.1.1节
网络架构 公式7基本上表明图1中每个蓝色节点的“输出概率”总和为1。实际上, β \beta β值可以被解释为跨越不同“时间步长”(层数)的不同“状态”(空间分辨率)之间的“迁移概率”。很直观地说,我们的目标是从头到尾找到“最大概率”的路径。使用经典的Viterbi算法可以有效地解码该路径,如我们的实现一样。
5.实验结果
在这里,我们报告我们的架构搜索实现细节以及搜索结果。然后,我们报告使用我们最好的架构在基准数据集上的语义分割结果。
5.1架构搜索实现细节
我们考虑网络中总共 L = 12 L = 12 L=12层,并且单元中的块个数为 B = 5 B = 5 B=5。网络级搜索空间有 2.9 × 1 0 4 2.9×10^4 2.9×104条不同的路径,单元结构的数量为 5.6 × 1 0 14 5.6×10^{14} 5.6×1014。所以联合分层搜索空间的大小约为 1 0 19 10^{19} 1019。
我们遵循通常的做法,即在将特征张量的高度和宽度减半时将滤波器的数量加倍。图1中每个蓝色节点的下采样率为 s s s,有 B × F × s B×F×s B×F×s个输出滤波器(output filters),其中 F F F是控制模型容量的乘法滤波器( filter multiplier)。在架构搜索中我们设置 F = 8 F=8 F=8。在 s 2 → s \frac{s}{2} \to s 2s→s的连接中设置卷积的步长为2,同时缩小空间分辨率,加倍滤波器数量。对于所有 2 s → s 2s \to s 2s→s的连接,双线性上采样后接 1 × 1 1 ×1 1×1的卷积,同时增大空间分辨率,减半滤波器数量。
[9]中使用的孔洞空间金字塔池化模块有5条分支:一个 1 × 1 1 ×1 1×1的卷积,三个 3 × 3 3 ×3 3×3有不同孔洞率的卷积,和一个池化的图像特征。在搜索过程中,我们使用简化的有3条分支的ASPP,只使用一个孔洞率为 96 s \frac{96}{s} s96的 3 × 3 3 ×3 3×3的卷积。每个ASPP分支滤波器的数量依旧是 B × F × s B×F×s B×F×s。
我们在Cityscapes数据集上进行用于图像语义分割的架构搜索。更具体地说,我们使用train_fine集中一半分辨率(512×1024)的图像进行随机图像裁剪,得到321×321图像。我们随机选择train_fine中一半的图像当做trainA,另一半为trainB(参加4.2节)。
在总数为40的epochs中进行架构搜索优化。由于GPU显存限制,设置batch size为2。当学习网络权重 w w w时,我们使用动量为0.9的随机梯度下降优化,学习率从0.025衰减到0.001,权值衰减率为0.0003。当学习架构编码 α , β \alpha,\beta α,β时,我们使用学习率为0.003,权值衰减率为0.001的Adam优化[36]。我们凭经验发现,如果在 w w w没有经过良好训练的情况下开始优化 α , β \alpha,\beta α,β,那么这种结构往往会陷入糟糕的局部最优。因为我们在经过20 epochs后才开始优化 α , β \alpha,\beta α,β。整个框架搜索优化在单个P100 GPU上需要耗时3天。图4显示在整个过程中验证集精度稳步提高。我们也尝试寻找更长的epochs(60,80,100),但没有观察到好处。
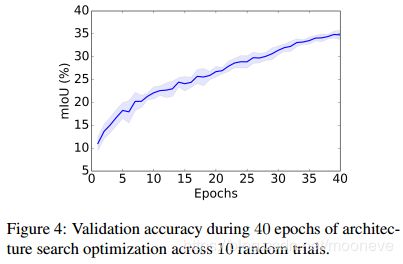
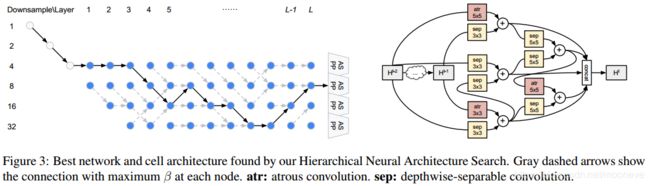
图3显示了找到的最佳架构。就网络级架构而言,在开始(保持以4的下采样时间更长)和结束(以8的下采样结束)时都优选更高的分辨率。我们还使用灰色虚线箭头显示每个节点上最大 β \beta β值的连接。我们观察到在前3/4层中有进行下采样,并在最后的1/4层中进行上采样的一般趋势。在单元级架构方面,经常使用孔洞卷积和深度可分卷积的结合,这表明已经学习了上下文的重要性。注意,很少发现孔洞卷积在用于图像分类的单元中是有用的。(在NASNet- {A,B,C}、PNASNet- {1,2,3,4,5}、AmoebaNet- {A,B,C}、ENAS、DARTS中,孔洞卷积仅在AmoebaNet-B的缩小单元中使用一次)
5.2语义分割结果
我们在Cityscapes[13],PASCAL VOC 2012[15],和ADE20K数据集上评估我们找到的最好的架构的性能。
我们遵循[9,11]中的相同训练协议。简单来说,在训练期间,我们采用初始学习率为0.05的多项式学习率[50],和大的裁剪图像(例如,Cityscapes上的769×769,以及PASCAL VOC 2012上的513×513和ADE20K的resized图像)。在训练阶段微调Batch normalization参数[32]。这些模型从头开始训练,在Cityscapes上进行1.5M迭代,在PASCAL VOC 2012上进行1.5M迭代,在ADE20K上进行4M迭代。
多项式学习率: l r = b a s e _ l r ∗ ( 1 − i t e r m a x i t e r ) p o w e r lr = base\_lr * (1 −\frac{iter }{maxiter }) ^ {power} lr=base_lr∗(1−maxiteriter)power power=0.9
我们采用类似于DeepLabv3 +的简单编码器 - 解码器结构[11]。具体来说,我们的编码器由我们发现的最佳网络架构与ASPP模块[8,9]组成,我们的解码器与DeepLabv3 +中的解码器相同,后者通过利用具有下采样率4的低级特征来恢复边界信息。此外,我们重新设计了具有三个3×3卷积的“枝干”结构(在第一和第三卷积中步长为2)。前两个卷积有64个滤波器,而第三个卷积有128个滤波器。这种“枝干”已在[87,77]中证明对分割有效。
5.2.1Cityscapes
Cityscapes[13]包含5000张高质量像素级标注的1024×2048图片(2975,500,和1525张分别用于训练集,验证集和测试集),以及大约20000张粗略标注的训练图片。遵循[13]中的评估标准,排除考虑空标签,剩下的19个语义标签用来进行评估。
在表2,我们报告了在Cityscapes验证集上的结果。与MobileNets[29,65]类似,我们通过改变filter multiplier F F F来改变模型容量(capacity)。如表中所示,更高的模型容量导致更好的性能,代价是速度更慢(由更大的Multi-Adds表示)。
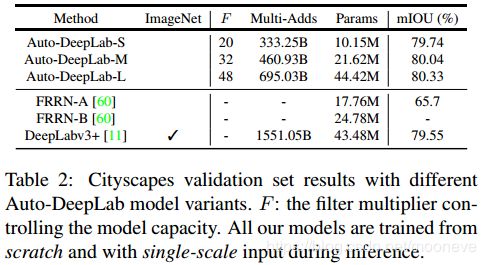
在表3,我们表明,当采用我们的轻量级模型变体Auto-DeepLab-S时,将训练迭代次数从500K增加到1.5M迭代可将性能提高2.8%。此外,采用Scheduled Drop Path[40,92]进一步提高了1.74%的性能,在Cityscapes验证集达到79.74%。

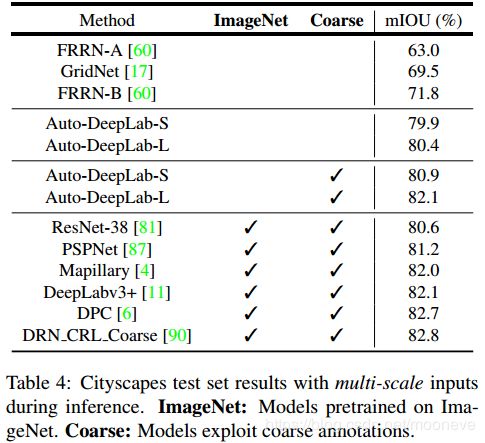
然后我们在表4中报告测试集结果。 在没有任何预训练的情况下,我们的最佳模型(Auto-DeepLab-L)明显优于FRNN-B [60] 8.6%和GridNet [17] 10.9%。使用额外的粗略标注进行训练,没有在ImageNet [64]预先训练的情况下,我们的模型Auto-DeepLab-L实现了82.1%的测试集性能,优于PSPNet [87]和Mapillary [4],并获得与DeepLabv3 + [11]相同的性能,同时比它减少了55.2%的Mutli-Adds计算。值得注意的是,我们的轻量级变体Auto-DeepLab-S在测试集上达到80.9%,与PSPNet相当,而仅使用10.15M参数和333.25B Multi-Adds。
5.2.2 PASCAL VOC 2012
PASCAL VOC 2012 [15]包含20个前景对象类和一个背景类。我们使用[23]提供的额外标注来扩充原始数据集,从而生成10582(train_aug)张训练图像。
在表5,我们报告测试集的结果。我们的最佳模型Auto-DeepLab-L,单尺度推理明显优于[19] 20.36%。此外,对于我们所有的模型变体,采用多尺度推理可将性能提高约1%。在COCO [46]上进一步预训练我们的模型进行4M次迭代可以显着提高性能。

最后,我们在表6中报告模型变体经过COCO预训练后在PASCAL VOC 2012测试集的结果。如表中所示,我们的最佳模型在测试集上的性能达到85.6%,优于RefineNet [44]和PSPNet [87]。我们的模型比表现优异的以Xception-65作为网络骨干的DeepLabv3 + [11]落后2.2%。我们认为PASCAL VOC 2012数据集太小,无法从头开始训练模型,在这种情况下,在ImageNet上进行预训练仍然是有益的。

5.2.3 ADE20K
ADE20K [89]拥有150个语义类别和高质量标注的20000张训练图像和2000张验证图像。在我们的实验中,图像都被调整大小,以便在训练期间长边是513。
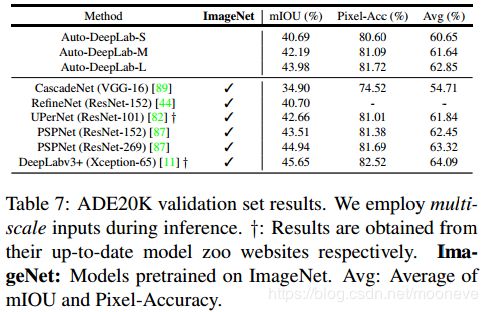
在表7中,我们报告验证集结果。我们的模型优于一些最先进的模型,包括RefineNet [44],UPerNet [82]和PSPNet(ResNet-152)[87]。然而,在没有任何ImageNet [64]预训练的情况下,我们的性能落后于 [11]的最新工作。
6.结论
在本文中,我们首次尝试将神经网络搜索技术从图像分类扩展到密集图像预测问题。我们承认空间分辨率变化的重要性,不固定在单元级上,将网络级整合到搜索空间中来体现架构变化。我们还开发了一种可微分的公式,它允许我们在两级分层搜索空间中实现高效(比DPC [6]快大约1000倍)的架构搜索。搜索的结果Auto-DeepLab是通过从头开始在基准语义数据集进行训练评估得来的。在Cityscapes上,Auto-DeepLab明显优于之前的最新技术8.6%,并且在利用粗略注释时与经过ImageNet预训练的顶级模型相当。在PASCAL VOC 2012和ADE20K上,Auto-DeepLab也优于多个经过ImageNet预训练的最先进模型。
未来的工作有很多可能的方向。在目前的框架内,目标检测等相关应用应该是合理的。我们还可以尝试以很小的计算开销解决不同层的单元架构 α \alpha α(参见[76])。除了当前的框架之外,更加通用和松弛的网络级搜索空间应该是有益的(参见3.2节)。

