高性能Mysql:B-TREE和B+-TREE

一、索引简介

数据库中，索引对于查询来说至关重要。它就像书籍里的目录一样，能在磁盘页面中迅速找到所需要的记录，能够将查询性能提高好几个数量级。所以索引是应对查询性能最有效的手段。下面从原理的角度分析mysql的集中索引类型。

二、B-TREE和B+-TREE的特点

首先明确一点，mysql中的索引是存储引擎实现的，而不是在服务器层实现的，所以每种存储引擎的索引实现方式可能不同，支持的索引类型也有可能不同。在各大数据库实现中，使用最多的就是B-TREE索引或者是B*TREE索引。

三、B-TREE索引

这里的B并不是binary的意思，而是balance（平衡树又称平衡多路查找树）的意思。

m阶的B-tree特性如下：

• 树种每个节点最多m个孩子，
• 除根节点和叶子节点外，至少两个孩子。
• 如果根节点不是叶子节点，则至少两个孩子。
• 所有叶子节点都出现在同一层，叶子节点不包含任何关键字信息
• 每个非终端结点中包含有n个关键字信息： (n，P0，K1，P1，K2，P2，……，Kn，Pn)。其中：
  a) Ki (i=1…n)为关键字，且关键字按顺序排序K(i-1)< Ki。
  b) Pi为指向子树根的接点，且指针P(i-1)指向子树种所有结点的关键字均小于Ki，但都大于K(i-1)。
  c) 关键字的个数n必须满足： ceil(m / 2)-1 <= n <= m-1。

B-tree中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然是不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

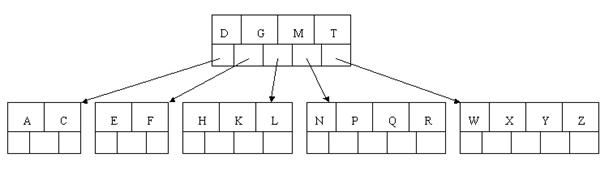
下面以一棵5阶B-tree实例进行讲解(如下图所示)：（重点看以下图）
其满足上述条件：除根结点和叶子结点外，其它每个结点至少有ceil(5/2)=3个孩子（至少2个关键字）；当然最多5个孩子（最多4个关键字）。下图中关键字为大写字母，顺序为字母升序。

插入（insert）操作：插入一个元素时，首先在B-tree中是否存在，如果不存在，即在叶子结点处结束，然后在叶子结点中插入该新的元素，注意：如果叶子结点空间足够，这里需要向右移动该叶子结点中大于新插入关键字的元素，如果空间满了以致没有足够的空间去添加新的元素，则将该结点进行“分裂”，将一半数量的关键字元素分裂到新的其相邻右结点中，中间关键字元素上移到父结点中（当然，如果父结点空间满了，也同样需要“分裂”操作），而且当结点中关键元素向右移动了，相关的指针也需要向右移。如果在根结点插入新元素，空间满了，则进行分裂操作，这样原来的根结点中的中间关键字元素向上移动到新的根结点中，因此导致树的高度增加一层。
咱们通过一个实例来逐步讲解下。插入以下字符字母到空的5阶B-tree中：C N G A H E K Q M F W L T Z D P R X Y S，5序意味着一个结点最多有5个孩子和4个关键字，除根结点外其他结点至少有2个关键字，首先，结点空间足够，4个字母插入相同的结点中，如下图：

当试着插入H时，结点发现空间不够，以致将其分裂成2个结点，移动中间元素G上移到新的根结点中，在实现过程中，咱们把A和C留在当前结点中，而H和N放置新的其右邻居结点中。如下图：

当插入E,K,Q时，则不需要任何分裂操作：

插入M需要一次分裂，注意M恰好是中间关键字元素，以致向上移到父节点中：

插入F,W,L,T不需要任何分裂操作：

插入Z时，最右的叶子结点空间满了，需要进行分裂操作，中间元素T上移到父节点中，注意通过上移中间元素，树最终还是保持平衡，分裂结果的结点存在2个关键字元素。

插入D时，导致最左边的叶子结点被分裂，D恰好也是中间元素，上移到父节点中，然后字母P,R,X,Y陆续插入不需要任何分裂操作。

最后，当插入S时，含有N,P,Q,R的结点需要分裂，把中间元素Q上移到父节点中，但是情况来了，父节点中空间已经满了，所以也要进行分裂，将父节点中的中间元素M上移到新形成的根结点中，注意以前在父节点中的第三个指针在修改后包括D和G节点中。这样具体插入操作的完成，下面介绍删除操作，删除操作相对于插入操作要考虑的情况多点。

删除(delete)操作： 首先查找B-tree中需删除的元素,如果该元素在B-tree中存在，则将该元素在其结点中进行删除，如果删除该元素后，首先判断该元素是否有左右孩子结点，如果有，则上移孩子结点中的某相近元素到父节点中，然后是移动之后的情况；如果没有，直接删除后，移动之后的情况.。

删除元素，移动相应元素之后，如果某结点中元素数目小于ceil(m/2)-1，则需要看其某相邻兄弟结点是否丰满（结点中元素个数大于ceil(m/2)-1），如果丰满，则向父节点借一个元素来满足条件；如果其相邻兄弟都刚脱贫，即借了之后其结点数目小于ceil(m/2)-1，则该结点与其相邻的某一兄弟结点进行“合并”成一个结点，以此来满足条件。那咱们通过下面实例来详细了解吧。

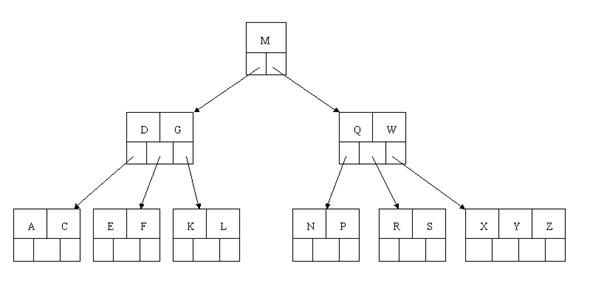
以上述插入操作构造的一棵5阶B-tree为例，依次删除H,T,R,E。

首先删除元素H，当然首先查找H，H在一个叶子结点中，且该叶子结点元素数目3大于最小元素数目ceil(m/2)-1=2，则操作很简单，咱们只需要移动K至原来H的位置，移动L至K的位置（也就是结点中删除元素后面的元素向前移动）

下一步，删除T,因为T没有在叶子结点中，而是在中间结点中找到，咱们发现他的继承者W(字母升序的下个元素)，将W上移到T的位置，然后将原包含W的孩子结点中的W进行删除，这里恰好删除W后，该孩子结点中元素个数大于2，无需进行合并操作。

下一步删除R，R在叶子结点中,但是该结点中元素数目为2，删除导致只有1个元素，已经小于最小元素数目ceil(5/2)-1=2,如果其某个相邻兄弟结点中比较丰满（元素个数大于ceil(5/2)-1=2），则可以向父结点借一个元素，然后将最丰满的相邻兄弟结点中上移最后或最前一个元素到父节点中，在这个实例中，右相邻兄弟结点中比较丰满（3个元素大于2），所以先向父节点借一个元素W下移到该叶子结点中，代替原来S的位置，S前移；然后X在相邻右兄弟结点中上移到父结点中，最后在相邻右兄弟结点中删除X，后面元素前移。

最后一步删除E，删除后会导致很多问题，因为E所在的结点数目刚好达标，刚好满足最小元素个数（ceil(5/2)-1=2）,而相邻的兄弟结点也是同样的情况，删除一个元素都不能满足条件，所以需要该节点与某相邻兄弟结点进行合并操作；首先移动父结点中的元素（该元素在两个需要合并的两个结点元素之间）下移到其子结点中，然后将这两个结点进行合并成一个结点。所以在该实例中，咱们首先将父节点中的元素D下移到已经删除E而只有F的结点中，然后将含有D和F的结点和含有A,C的相邻兄弟结点进行合并成一个结点。

看看上图，对于这种特殊情况，你立即会发现父节点只包含一个元素G，没达标，这是不能够接受的。如果这个问题结点的相邻兄弟比较丰满，则可以向父结点借一个元素。假设这时右兄弟结点（含有Q,X）有一个以上的元素（Q右边还有元素），然后咱们将M下移到元素很少的子结点中，将Q上移到M的位置，这时，Q的左子树将变成M的右子树，也就是含有N，P结点被依附在M的右指针上。所以在这个实例中，咱们没有办法去借一个元素，只能与兄弟结点进行合并成一个结点，而根结点中的唯一元素M下移到子结点，这样，树的高度减少一层。

四、B+ -TREE

B-tree索引存储的是key-data形式，而B+tree存储的key形式，没有data
一般数据库采用的是B+Tree，而且经过了一些优化，比如在叶子节点上增加了顺序访问指针，提高区间查询效率。比如：查询首字母为f~t的所有单词。那么只需查到f开头的第一个单词fabric，然后沿着叶子节点的开始遍历，直到找到最后一个以t开头的单词为止。

B+tree特性：

• 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
• 不可能在非叶子结点命中；（非叶子节点值存储指向数据的指针，而B-tree中非叶子节点也可以存储数据）
• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
• 更适合文件索引系统；

Tips:为什么更多的都是采用B+-tree,效率高在哪里？

1.B+-tree内部节点没有存储具体data，所以比B-tree小。把同一节点的data放在同一盘块中，能降低IO读写次数。

2.B+-tree查询效率更加稳定，由于任何关键字查找必须走从根节点到叶子节点，效率会稳定。

3.B+-tree的叶子节点是链表有序，在做范围查询的时候速度非常快。 例如上图中如果要查询key为从18到49的所有数据记录，当找到18后，只需顺着节点和指针顺序遍历就可以一次性访问到所有数据节点就可以。