深度学习中的优化问题
文章目录
- 一、优化问题简介及挑战
- 1、优化问题简介
- 2、优化问题中的两个挑战
- (a)、局部最小值
- (b)、鞍点
- 二、各种参数优化算法
- 1、Mini-batch SGD + LR Decay
- 2、Adagrad
- 3、Adadelta
- 4、RMSProp
- 5、Momentum(动量法)
- 6、Adam
- 三、优化算法总结
- 四、参考资料
一、优化问题简介及挑战
1、优化问题简介
- 绝大多数深度学习中的目标函数都很复杂。因此,很多优化问题
并不存在解析解,而需要使用基于数值方法的优化算法(eg:SGD)找到近似解。这类优化算法一般通过不断迭代更新解的数值来找到近似解。 - 这里我们简单解释一下:梯度下降算法是如何使损失函数的值一步步降低的?
-
假设 C ( v ) C(v) C(v) 为我们的损失函数,且只有两个变量 v 1 v1 v1 和 v 2 v2 v2,我们想找到 C C C 的全局最小值。当我们在 v 1 v1 v1 和 v 2 v2 v2 方向分别将球体移动一个很小的量,即 Δ v 1 \Delta v1 Δv1 和 Δ v 2 \Delta v2 Δv2 时,球体将会发生什么情况?可微与偏导存在的关系定理 告诉我们 C C C 将会有如下变化:
Δ C ≈ ∂ C ∂ v 1 Δ v 1 + ∂ C ∂ v 2 Δ v 2 \Delta C \approx \frac{\partial C}{\partial v_1} \Delta v_1 + \frac{\partial C}{\partial v_2} \Delta v_2 ΔC≈∂v1∂CΔv1+∂v2∂CΔv2 -
我们要寻找一种选择 Δ v 1 \Delta v_1 Δv1 和 Δ v 2 \Delta v_2 Δv2 的方法
使得Δ C \Delta C ΔC为负,定义 Δ v \Delta v Δv 为 v v v 变化的向量、 ∇ C \nabla C ∇C 来表示梯度向量,如下:
Δ v = ( Δ v 1 , Δ v 2 ) T \Delta v = (\Delta v_1, \Delta v_2)^T Δv=(Δv1,Δv2)T∇ C = ( ∂ C ∂ v 1 , ∂ C ∂ v 2 ) T \nabla C = \left( \frac{\partial C}{\partial v_1}, \frac{\partial C}{\partial v_2} \right)^T ∇C=(∂v1∂C,∂v2∂C)T
-
有了这些定义, Δ C \Delta C ΔC 的表达式可以被重写为:
Δ C ≈ ∇ C ⋅ Δ v \Delta C \approx \nabla C \cdot \Delta v ΔC≈∇C⋅Δv -
假设我们选取 Δ v \Delta v Δv 如下(原则: 使得损失函数总能因为我们的选择而下降,且是我们当前这一点下降最快的方向):
Δ v = − η ∇ C \Delta v = -\eta \nabla C Δv=−η∇C -
那么 Δ C ≈ − η ∇ C ⋅ ∇ C = − η ∥ ∇ C ∥ 2 \Delta C \approx -\eta \nabla C \cdot \nabla C = -\eta\|\nabla C\|^2 ΔC≈−η∇C⋅∇C=−η∥∇C∥2(其中, η \eta η 被称为学习率)。由于 ∥ ∇ C ∥ 2 ≥ 0 \| \nabla C \|^2 \geq 0 ∥∇C∥2≥0,这保证了 Δ C ≤ 0 \Delta C \leq 0 ΔC≤0。如果我们上述方程的规则去改变 v v v,那么 C C C 会一直减小,不会增加(当然,要满足方程的近似约束: Δ v \Delta v Δv 要足够小,这也是学习率和梯度都不能太大的道理 )。于是我们就可以按照如下的规则来更新模型的参数( Δ v \Delta v Δv 表示小球要往什么方向走,走多远):
v ′ = v − η ∇ C v' = v -\eta \nabla C v′=v−η∇C

-
2、优化问题中的两个挑战
- 优化问题中的两个挑战:
局部最小值和鞍点。这两种情况都会造成梯度接近或变成零,从而使得网络很难继续优化。
- 低维空间的非凸优化问题:主要是存在一些
局部最优点。采用梯度下降方法时,不合适的参数初始化会导致陷入局部最优点,因此主要的难点是如何选择初始化参数和逃离局部最优点。- 高维空间中非凸优化的难点:并不在于如何逃离局部最优点,而是
如何逃离鞍点。鞍点(saddle point)是梯度为0,但是在一些维度上是最高点,在另一些维度上是最低点。
(a)、局部最小值
绝大多数深度学习的目标函数有若干局部最优值。当一个优化问题的数值解在局部最优解附近时,由于梯度接近或变成零,最终得到的数值解可能只令目标函数局部最小化而非全局最小化。

(b)、鞍点
梯度接近或变成零可能是由于当前解在局部最优解附近所造成的。事实上,另一种可能性是当前解在鞍点附近。由于大多数深度学习模型参数都是高维的,因此,目标函数的鞍点往往比局部最小值更常见。


二、各种参数优化算法
优化算法的主要区别在于怎么调节学习率和动量(本质上还是调节的梯度-->可正可负)
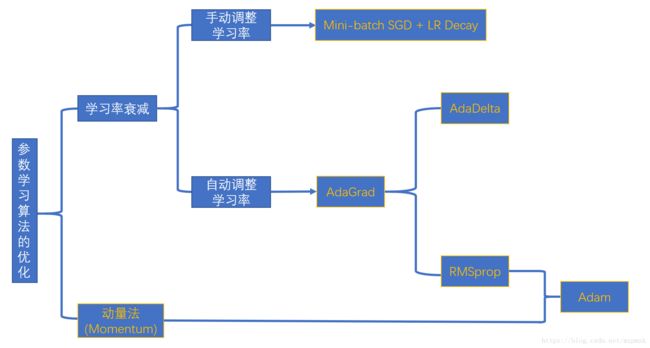
-
学习率衰减(Learning Rate Decay)
- 如下图所示,学习率正好时,参数 x x x 会沿着梯度方向不断更新,直至全局最优;学习率过大可能会造成 x x x 迈过(overshoot)最优解,甚至不断发散而无法收敛。从经验上来看,学习率在训练开始阶段要保持相对大些,从而保证
收敛速度,在训练后期模型收敛到最优点附近时,学习率要设小一些,从而避免来回震荡。所以,实践中我们经常随着训练的不断进行而逐渐减小学习率。 - 这是因为: 我们是对整个训练集进行随机采样 mini-batch,这会在优化时引入一些噪声,而这些噪声并不会在极小值点消失,可能会造成
来回震荡。 - 解决办法: 手动调整学习率(
Mini-batch SGD + LR Decay)或者自动调整学习率(AdaGrad, AdaDelta, RMSprop, Adam)

- 如下图所示,学习率正好时,参数 x x x 会沿着梯度方向不断更新,直至全局最优;学习率过大可能会造成 x x x 迈过(overshoot)最优解,甚至不断发散而无法收敛。从经验上来看,学习率在训练开始阶段要保持相对大些,从而保证
-
动量(Momentum)
- 通常我们会使用小批量随机梯度下降(Mini-Batch SGD)优化算法,但它每次迭代时使用的训练数据都是随机选取的,这样会引入一些噪声,而且其每次参数更新都是沿着梯度下降最快的方向,此方向仅
仅取决于当前的位置,这可能会带来一些问题,比如陷入局部极小值附近,开始来回震荡不能达到最小值。 - 解决办法:
Momentum 优化算法(可以配合手动调整 LR Decay 使用)或者Adam 优化算法
- 通常我们会使用小批量随机梯度下降(Mini-Batch SGD)优化算法,但它每次迭代时使用的训练数据都是随机选取的,这样会引入一些噪声,而且其每次参数更新都是沿着梯度下降最快的方向,此方向仅
1、Mini-batch SGD + LR Decay
TF 中学习率的设置有以下几种函数可以调用,另外我们可以参考下 caffe 中学习率的设置
- tf.train.exponential_decay 、 tf.train.inverse_time_decay、tf.train.natural_exp_decay
- tf.train.piecewise_constant、tf.train.polynomial_decay
2、Adagrad
- 在我们之前的优化算法中,无论是梯度下降、随机梯度下降、小批量随机梯度下降还是使用动量法,模型参数中的每一个元素在相同时刻都使用同一个学习率来自我迭代。Adagrad就是一个在迭代过程中不断自我调整学习率,并让模型参数中
每个元素都使用不同学习率的优化算法。 - 它的缺点是:学习率是不断的单调下降的,当经过一定次数的迭代依然没有找到最优点时,由于此时的
学习率已经非常小了很难继续找到最优点。 - 现在几乎
不再使用此算法,对其改进的优化算法有:Adadelta 和 RMSProp。

3、Adadelta
- Adadelta 优化算法是基于Adagrad 进行改进的,它没有学习率参数,主要是使用了梯度平方(按元素计算)和参数更新差值 g t ′ g_t^{\prime} gt′ 平方的指数衰减滑动平均(由 Adagrad 中的累积变为滑动平均),使得学习率在迭代过程中既可以变小又可以变大,从而自适应的调整学习率(每个元素都使用不同学习率)。而且,此算法
无需手动设置全局的学习率、对含噪声和较大的梯度都具有鲁棒性。其参数更新规则如下所示:
G t = ρ G t − 1 + ( 1 − ρ ) g t ⊙ g t G_t = \rho G_{t-1} + (1 - \rho) g_t \odot g_t Gt=ρGt−1+(1−ρ)gt⊙gt
g t ′ = Δ θ t − 1 ′ + ϵ G t + ϵ ⊙ g t g_t^{\prime} = \frac{\sqrt{\Delta{\theta_{t-1}^\prime} + \epsilon}}{\sqrt{G_t + \epsilon}} \odot {g_t} gt′=Gt+ϵΔθt−1′+ϵ⊙gt
Δ θ t ′ = ρ Δ θ t − 1 ′ + ( 1 − ρ ) g t ′ ⊙ g t ′ \Delta{\theta_t}^\prime = \rho \Delta{\theta_{t-1}^\prime} + (1 - \rho) {g_t}^\prime \odot {g_t}^\prime Δθt′=ρΔθt−1′+(1−ρ)gt′⊙gt′
θ t = θ t − 1 − g t ′ \theta_t = \theta_{t-1} - g_t^{\prime} θt=θt−1−gt′
- 其中, G t G_t Gt 是当前时刻梯度平方(按元素计算)的指数衰减滑动平均, G t − 1 G_{t-1} Gt−1 是上一时刻梯度平方(按元素计算)的指数衰减滑动平均, g t g_t gt 是当前时刻的梯度, ρ \rho ρ 是衰减率,控制着历史梯度信息滑动平均的长度范围; g t ′ g_t^{\prime} gt′ 是当前时刻参数的更新量, Δ θ t − 1 ′ \Delta{\theta_{t-1}^\prime} Δθt−1′ 是上一时刻参数更新量的指数衰减滑动平均, ϵ \epsilon ϵ 是为了保持数值稳定性而引入的一个非常小的常数,一般取 1 0 − 6 10^{-6} 10−6; Δ θ t ′ \Delta{\theta_{t}^\prime} Δθt′ 是当前时刻参数更新量的指数衰减滑动平均,
用于动态的设定全局学习率。
4、RMSProp
- RMSProp 是 Geoff Hinton 提出的一种基于 Adagrad 进行改进的优化算法,它主要是使用了
梯度平方(按元素计算)的指数衰减滑动平均(由 Adagrad 中的累积变为滑动平均),使得学习率在迭代过程中既可以变小又可以变大,从而自适应的调整学习率(每个元素都使用不同学习率)。其参数更新规则如下所示:
G t = γ G t − 1 + ( 1 − γ ) g t ⊙ g t G_t = \gamma G_{t-1} + (1 - \gamma) g_t \odot g_t Gt=γGt−1+(1−γ)gt⊙gt
θ t = θ t − 1 − η G t + ϵ ⊙ g t \theta_t = \theta_{t-1} - \frac{\eta}{\sqrt{G_t + \epsilon}} \odot g_t θt=θt−1−Gt+ϵη⊙gt
- 其中, G t G_t Gt 是当前时刻梯度平方(按元素计算)的指数衰减滑动平均, G t − 1 G_{t-1} Gt−1 是上一时刻梯度平方(按元素计算)的指数衰减滑动平均, g t g_t gt 是当前时刻的梯度, γ \gamma γ 是衰减率,控制着历史梯度信息滑动平均的长度范围,一般取 0.9 0.9 0.9, ϵ \epsilon ϵ 是为了保持数值稳定性而引入的一个非常小的常数,一般取 1 0 − 6 10^{-6} 10−6, η \eta η 是学习率。
5、Momentum(动量法)
- 基于动量(Momentum)的小批量随机梯度下降每次参数的更新
不仅仅取决于当前的梯度,还取决过去各个梯度在各个方向上的值,可以看作是对梯度做指数衰减滑动平均。假如,在某个时间段内一些参数的梯度方向与之前的不一致时,那么真实的参数更新幅度会变小;相反,若在某个时间段内的参数的梯度方向都一致,那么其真实的参数更新幅度会变大,起到加速收敛的作用。在迭代后期,由于随机噪声问题,经常会在收敛值附近震荡,动量法会起到减少震荡(不同方向上的梯度相互抵消),增加稳定性的作用。它基本解决了小批量随机梯度下降优化算法的问题,所以本节将使用基于动量的小批量随机梯度下降对网络进行优化,其参数更新规则如下所示:
v t = γ v t − 1 + g t v_t = \gamma v_{t-1} +g_t vt=γvt−1+gt
θ t = θ t − 1 − η v t \theta_t = \theta_{t-1} - \eta v_t θt=θt−1−ηvt
- 其中, v t v_t vt 是当前时刻梯度的指数衰减滑动平均, v t − 1 v_{t-1} vt−1 是上一时刻梯度的指数衰减滑动平均, g t g_t gt 是当前时刻的梯度, γ \gamma γ 是动量因子,控制着历史梯度信息对当前时刻梯度指数衰减滑动平均影响的大小, η \eta η 是学习率。需要注意的是,这个指数衰减滑动平均实际上是对 g t 1 − γ \frac{g_t}{1-\gamma} 1−γgt 做的,假如 γ = 0.9 \gamma = 0.9 γ=0.9,那么当
达到一定的训练次数后,梯度更新值将会扩大到原来的 1 1 − γ = 10 \frac{1}{1-\gamma} = 10 1−γ1=10 倍,所以如果要增加动量因子 γ \gamma γ 的话,最好是相应地减少学习率 η \eta η 的值。 - 结合论文深入理解:
- Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming
faster and faster on the way (until it reaches its terminal velocity, if there is air resistance) - The same thing happens to our parameter updates: The momentum term increases for dimensions whose gradients point in the same directions and reduces updates for dimensions whose gradients change directions. As a result, we gain faster convergence and reduced oscillation.

- Essentially, when using momentum, we push a ball down a hill. The ball accumulates momentum as it rolls downhill, becoming
6、Adam
- Adam 可以看作是一种
基于动量(Momentum)的梯度下降算法和 RMSprop 算法结合(+bias correction)的优化算法。它分别使用了梯度和梯度平方(按元素计算)的指数衰减滑动平均,使得模型不但可以使用动量作为参数更新的方向,还可以自适应的调整每个参数的学习率。其参数更新规则如下所示:
M t = β 1 M t − 1 + ( 1 − β 1 ) g t M_t = \beta_1 M_{t-1} + (1 - \beta_1) g_t Mt=β1Mt−1+(1−β1)gt
G t = β 2 G t − 1 + ( 1 − β 2 ) g t ⊙ g t G_t = \beta_2 G_{t-1} + (1 - \beta_2) g_t \odot g_t Gt=β2Gt−1+(1−β2)gt⊙gt
M t ^ : = M t 1 − β 1 t \hat{M_t} := \frac{M_t}{1 - \beta_1^t} Mt^:=1−β1tMt
G t ^ : = G t 1 − β 2 t \hat{G_t} := \frac{G_t}{1 - \beta_2^t} Gt^:=1−β2tGt
θ t = θ t − 1 − η M t ^ G t ^ + ϵ \theta_t = \theta_{t-1} - \frac{\eta \hat{M_t}}{\sqrt{\hat{G_t} + \epsilon}} θt=θt−1−Gt^+ϵηMt^
- 其中, M t M_t Mt 和 G t G_t Gt 分别是是当前时刻梯度和梯度平方(按元素计算)的指数衰减滑动平均, M t − 1 M_{t-1} Mt−1 和 G t − 1 G_{t-1} Gt−1 分别是上一时刻梯度和梯度平方(按元素计算)的指数衰减滑动平均, g t g_t gt 是当前时刻的梯度, β 1 \beta1 β1 和 β 2 \beta2 β2 是梯度和梯度平方的滑动平均衰减率,控制着历史梯度信息滑动平均的长度范围; M t ^ \hat{M_t} Mt^ 和 G t ^ \hat{G_t} Gt^ 分别是 M t M_t Mt 和 G t G_t Gt 的偏差修正,这样做是为了减轻 M t M_t Mt 和 G t G_t Gt 初始化为零在迭代初期对它们的指数衰减滑动平均的影响,从公式中可以看到,当 0 ≤ β 1 , β 2 < 1 0 \leq \beta_1, \beta_2 < 1 0≤β1,β2<1 时(算法作者建议将它们分别设为
0.9 和 0.99)且迭代前期 t t t 比较小时,此公式可以起到偏差修正的作用,当迭代后期 t t t 比较大时,偏差修正几乎就不再对其有影响; ϵ \epsilon ϵ 是为了保持数值稳定性而引入的一个非常小的常数,一般取 1 0 − 6 10^{-6} 10−6, η \eta η 是初始学习率。
三、优化算法总结
-
「随机降低方差难」:随机梯度下降难以在迭代过程中不断降低梯度的方差
-
「引入动量别弯慢」:弯是指震荡,慢是指收敛慢。动量法
减少了震荡,加速了收敛。 -
如果数据是稀疏的,优先考虑自适应学习率的算法,即 Adam, Adadelta, RMSprop。
四、参考资料
1、https://zh.gluon.ai/chapter_optimization/index.html
2、TensorFLow 中的参数学习算法

