一笔画完(微信小程序游戏)攻略
这个游戏和我攻略过的另外2个游戏相关性较高:同一个世界、一笔画2 攻略
和一笔画2不一样,一笔画完这个游戏是给出了起点的。
本文介绍了这个游戏的规律和策略,总结成了五个定理和一个三个策略。
首先定义几个名词:
邻居:每个点最多有4个邻居,即上下左右
度:邻居的个数,范围是1-4
格子总数:开局状态所有格子的数量
唯一终点:有的局面有唯一终点,即只有一个格子可以是终点。有的局面有多个格子可以是终点。
路径:由一连串相邻的点构成的有序列表。
然后我们来解决第一个问题,如何寻找终点?
定理一:起点到终点的曼哈顿距离的奇偶性和格子总数的奇偶性不同。
利用这个定理,就可以排除一半的格子了。
定理二:如果有个格子(不是起点)度为1,那么它就是唯一终点。
接着我介绍一个有效的化简局面的方法:
定理三:如果一个格子(不是起点或终点)的度为2,那么它的2个邻居在路径中一定是和它相邻的。
以第50关为例:
首先利用定理二很容易找到格子E就是唯一终点。
接着我们可以找到7个可以应用定理三的格子
于是我们得到:
到这里答案就一目了然了。
顺便解释一下定理一:起点到终点的曼哈顿距离是3+4=7,格子总数是26,奇偶性是不同的。
因为度很重要,所以这里不得不介绍一个重要的思想:
策略一:度的动态算法:
在寻找某条路径的时候,经过推理我们判断出格子A和它的邻居B在这条路径中的排序是不相邻的,那么在计算A的度的时候可以直接不算入B
注1:不一定在所有路径中A和B都不相邻。
注2:如果经过推理我们判断出格子A和它的邻居B在任何路径中的排序都是不相邻的,那么在计算A的度的时候可以直接不算入B,这不影响我们找到任何一条路径。
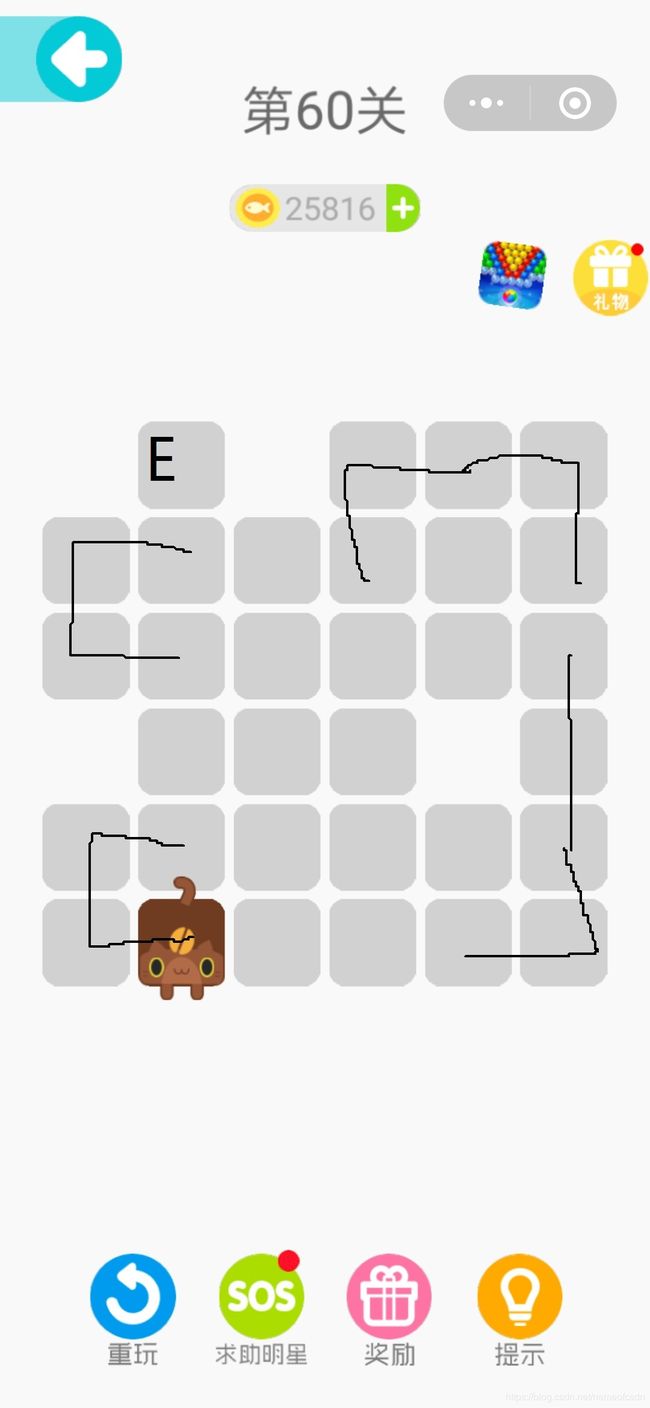
以第60关为例:
用定理二很容易找到格子E就是唯一终点,再用定理三得到:
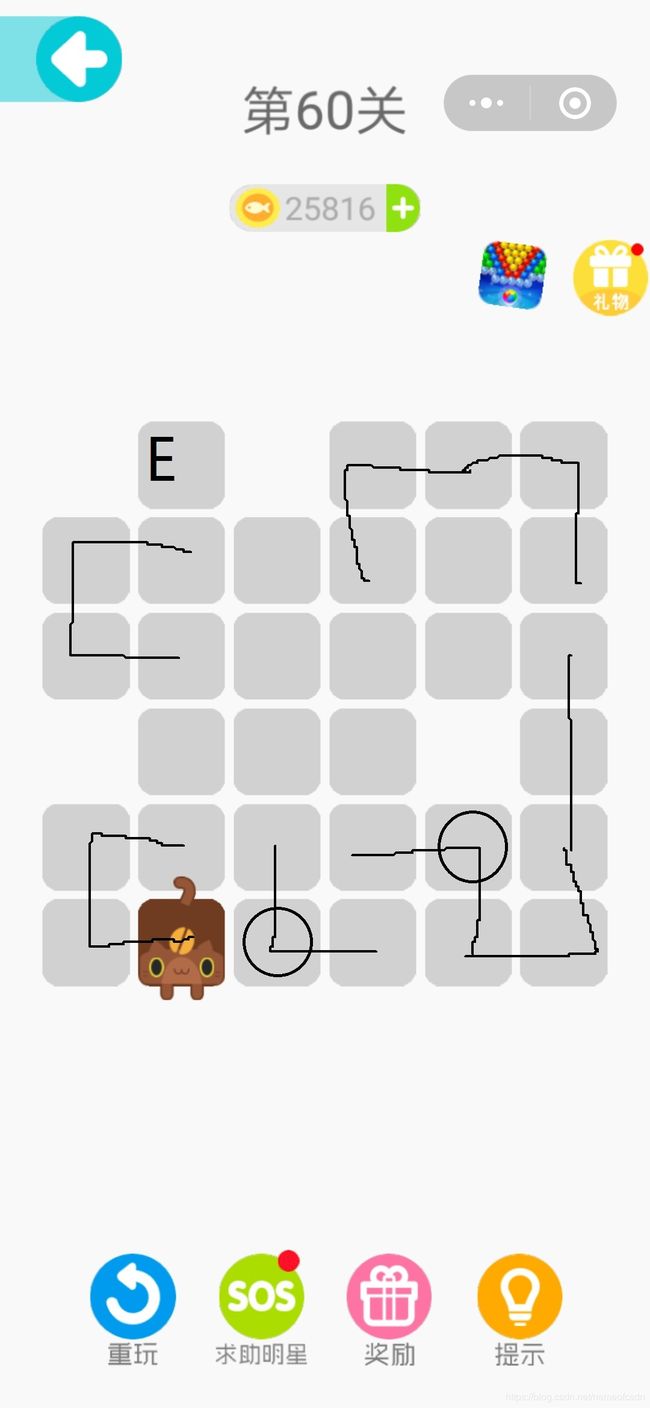
接着我们发现有2个格子(画圆圈的格子)可以利用度的动态算法把度看做2,于是再利用定理三得到:
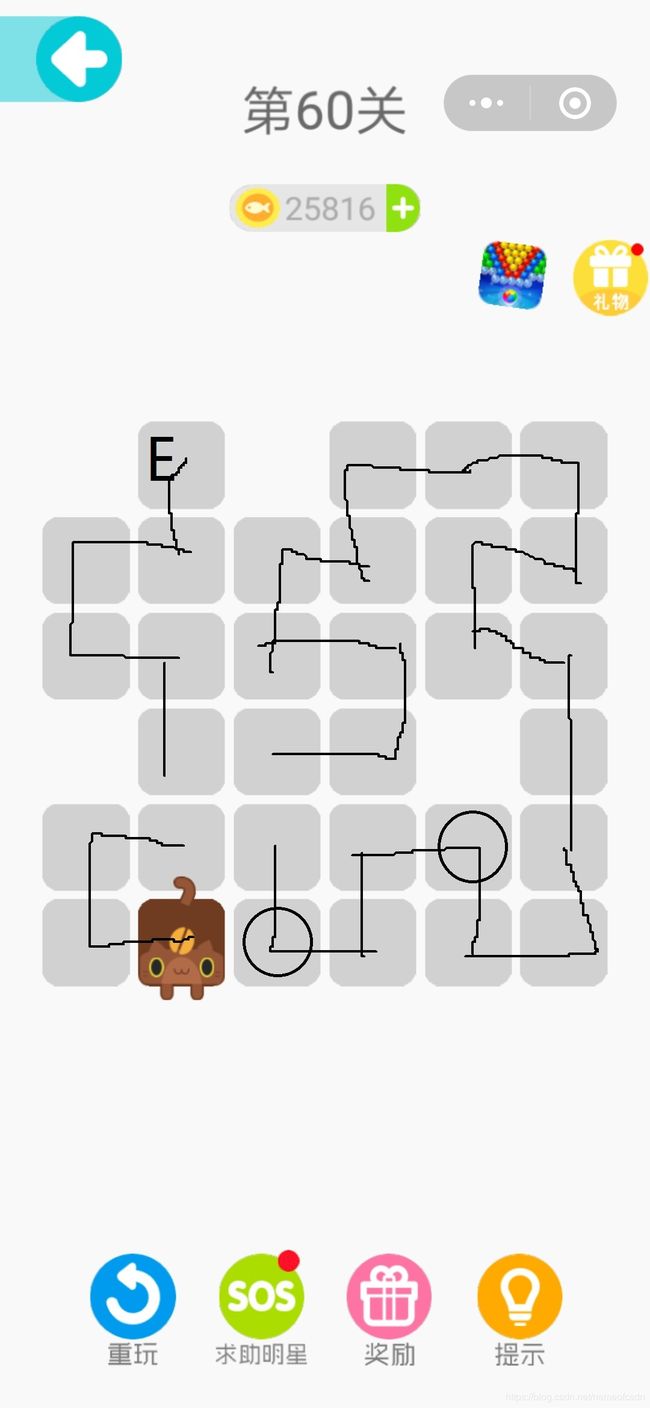
重复这个过程得到:
再重复这个过程得到:
至此,唯一路径就直接得到了。
之所以是唯一路径,参考度的动态算法的注2
接着再介绍一个我发明的非常厉害的分割法:
定理四(分割法一):
如果有一条分割线(不一定是直线)不穿过格子只经过格子之间的缝隙,把整个局面分为A、B两块,
且A块中只有1个格子P1和这条分割线相邻,P1唯一的属于B块的邻居是P2,
那么起点S和终点E不在分割线同一侧,且路径一定跨过这条分割线1次。
而且,AB两块可以分别求子路径,P1和P2分别是新增起点和新增终点,最后把P1和P2相连,2条子路径合并得到的最终路径即为所求。
定理五(分割法二):
如果有一条分割线(不一定是直线)不穿过格子只经过格子之间的缝隙,把整个局面分为A、B两块,
如果AB都有且只有2个格子和这条分割线相邻,此时假设起点S在A块,A块和分割线相邻的格子是P1、P2,B块和分割线相邻的格子是P3、P4,且P1和P3相邻,P2和P4相邻(P1P2不一定相邻,P3P4不一定相邻)
那么根据起点和终点的位置可以分为两种情况:
(1)起点和终点都在A侧,那么路径一定跨过这条分割线2次,
而且AB两块可以分别找到满足下面条件的子路径:A块中P1和P2相连(即使P1P2不是邻居),B块中P3和P4即为起点和终点
于是2条子路径即可merge为最终路径。
(2)起点和终点不在同一侧,那么路径一定跨过这条分割线1次,
于是要么P1和P3最终不相邻,要么P2和P4最终不相邻,于是利用度的动态算法,这种情况即退化为定理四。
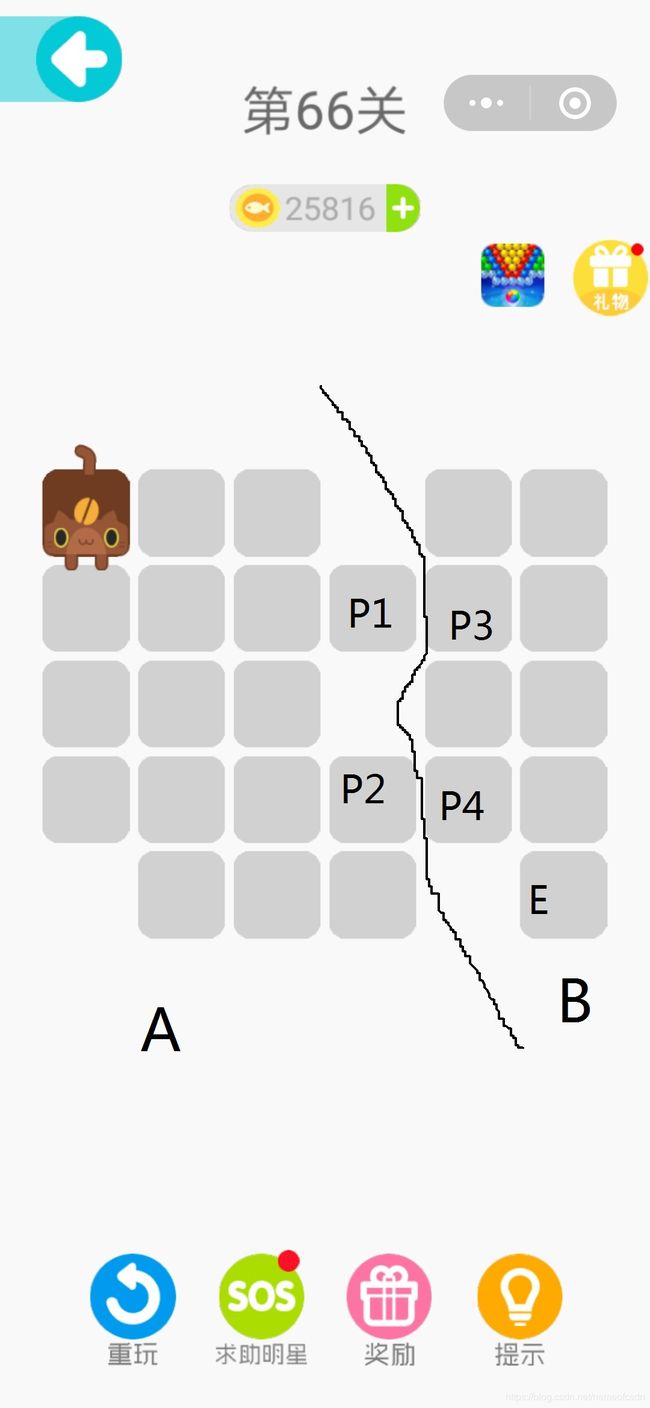
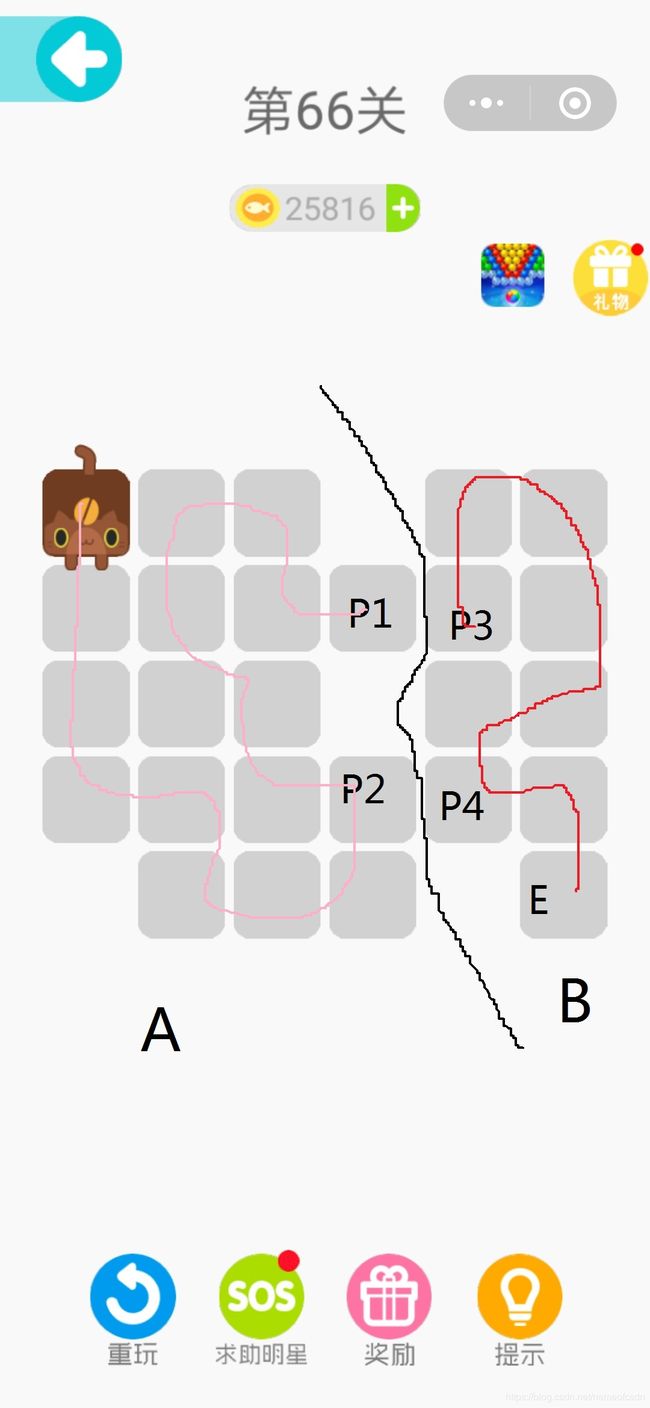
以第66关为例:
画一条非常厉害的分割线:
那么这就是定理五的第(2)种情况
因为根据定理三可知,P1和P3是相邻的,所以P2和P4是不相邻的。
于是退化为定理四,在A块寻找S到P1的路径,在B块寻找P3到E的路径,然后merge得到最终路径。
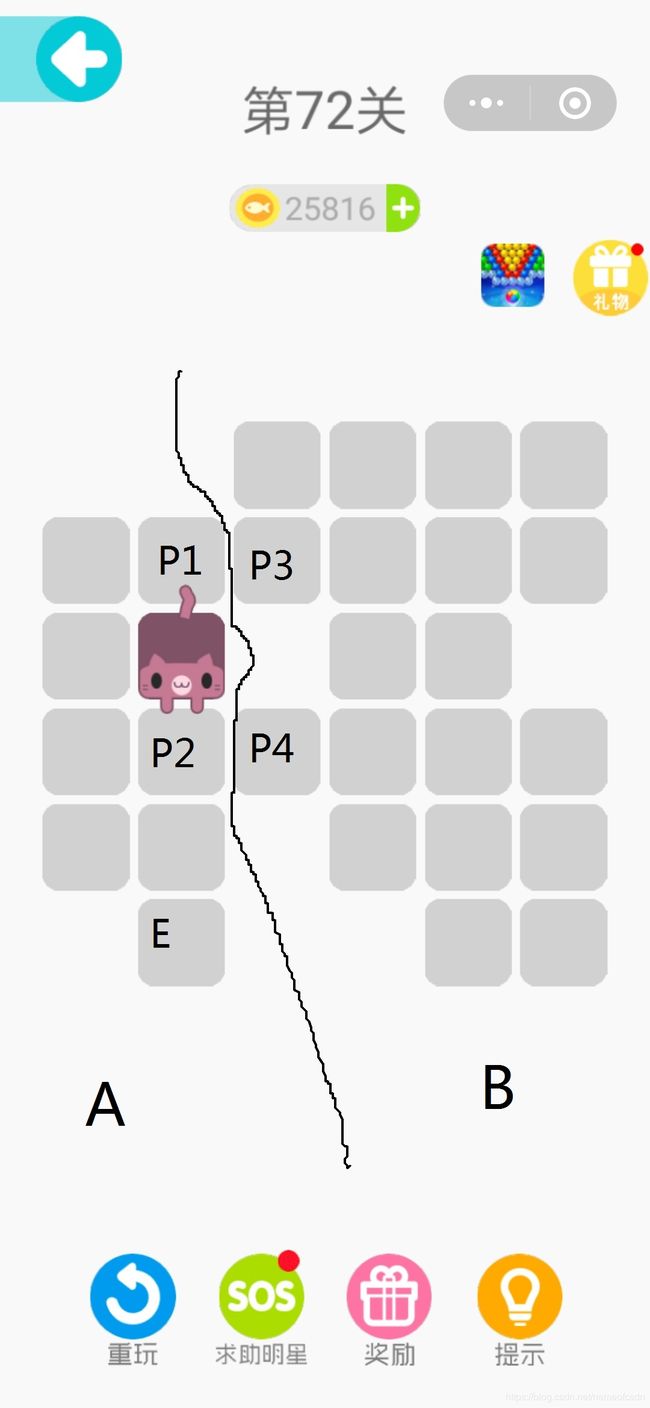
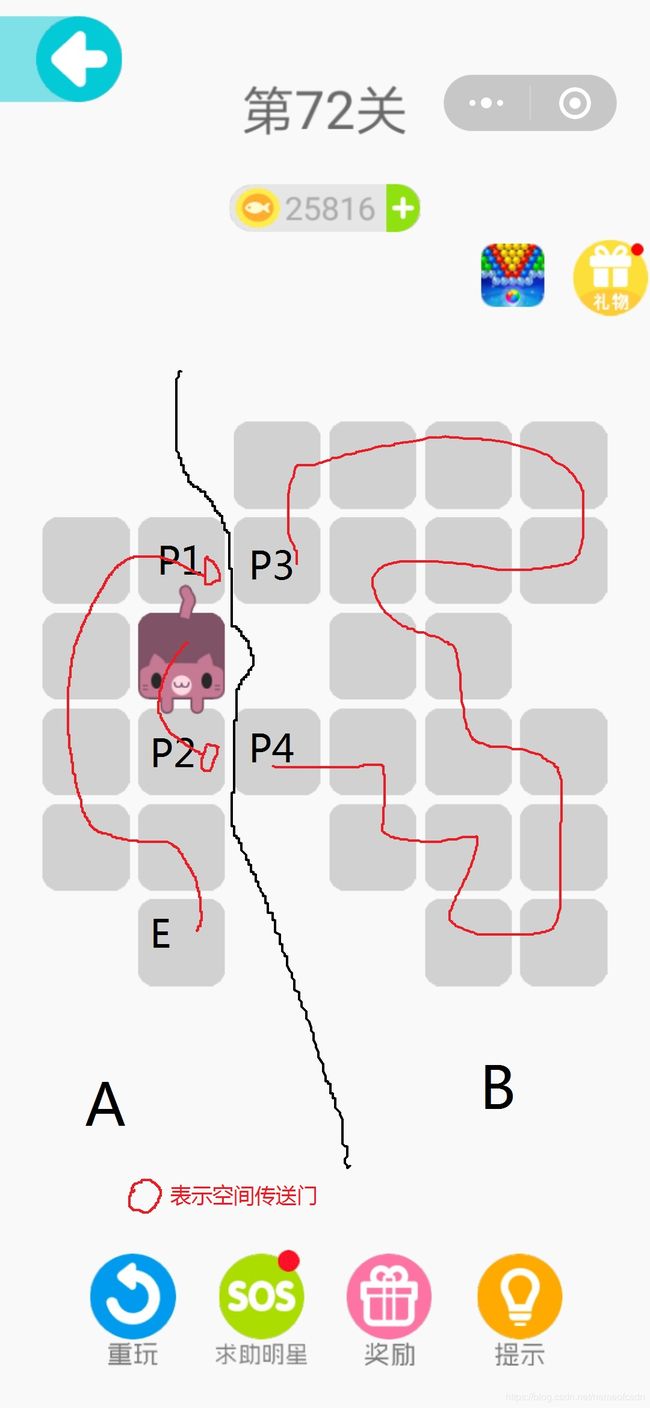
再以图72关为例:
画一条非常厉害的分割线:
那么这就是定理五的第(1)种情况
接着我介绍一个非常常见的场景:
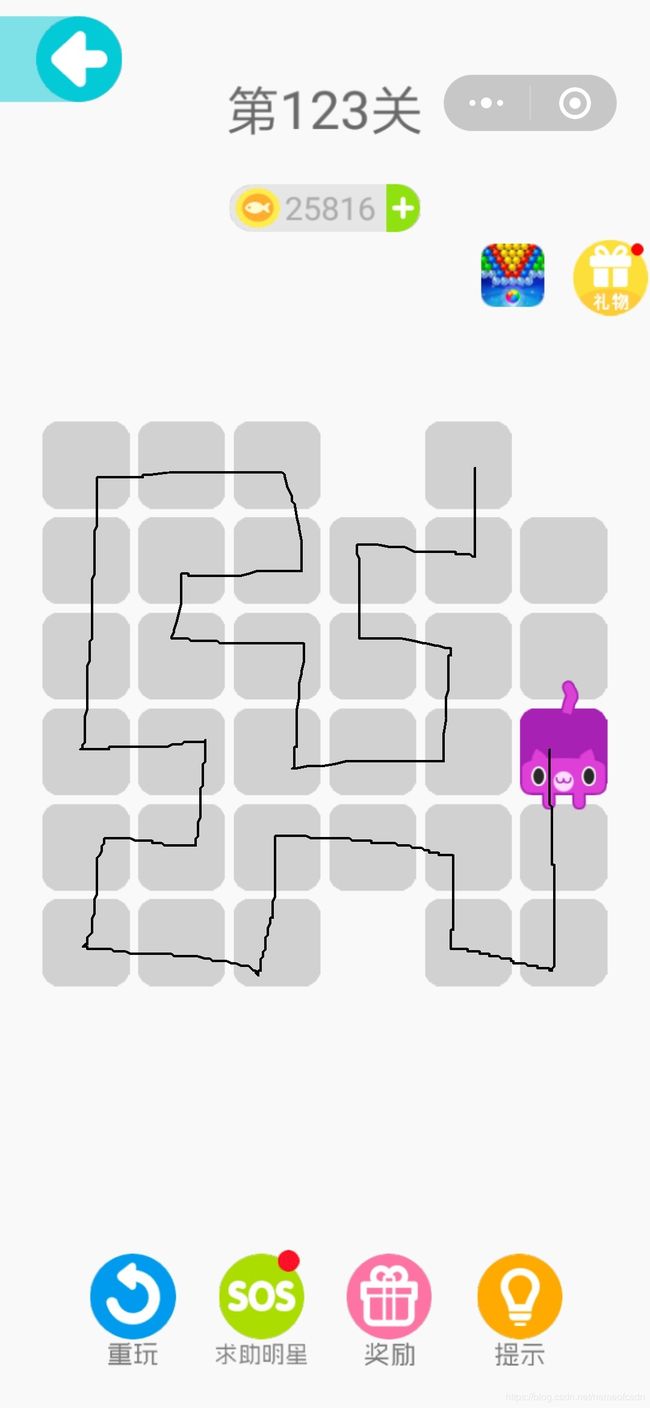
经常遇到,起点走到终点,却缺了2个格子的情况,例如第123关:
这时,我们可以通过策略二——变形,解决这个问题:
策略二比较简单,我就不描述了。
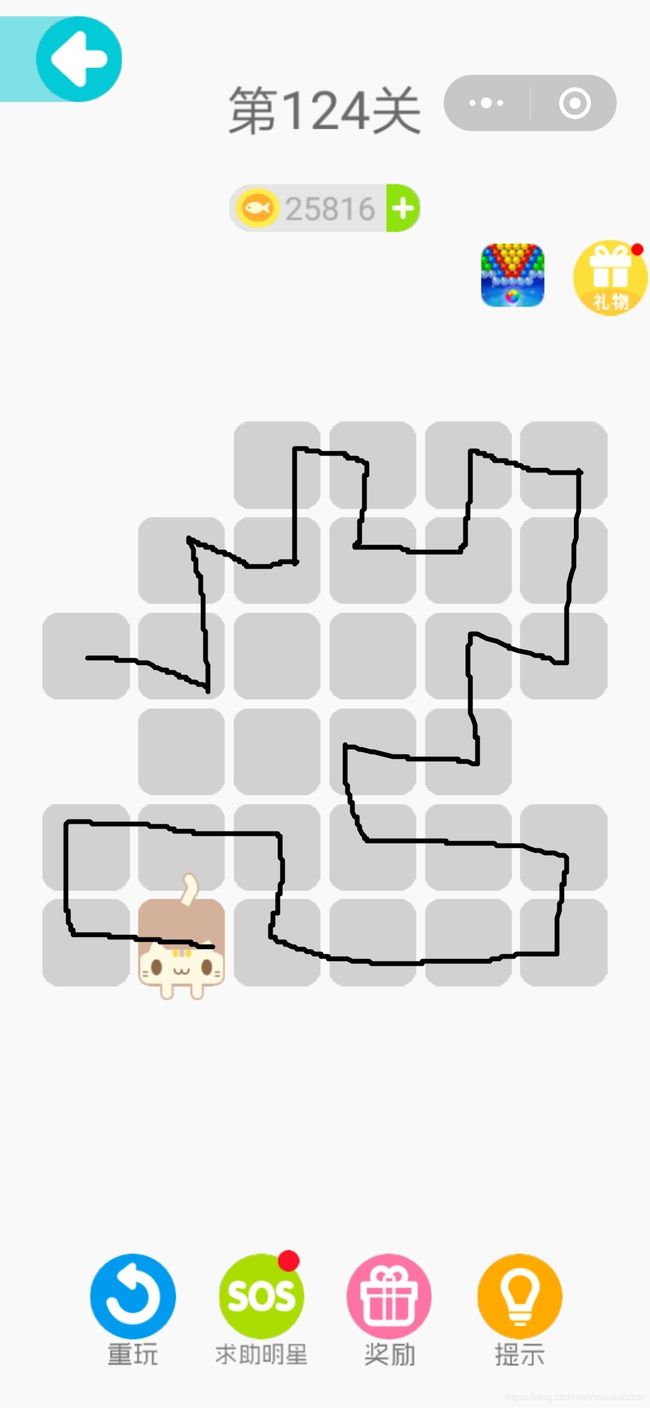
再比如第124关:
变形为:
再来介绍策略三:边界切割:
如果起点或者终点在角落或靠近角落的边界位置,可以把这个格子所在的最旁边两行或者两列切割出来,看看能否通过分块解决这个问题。
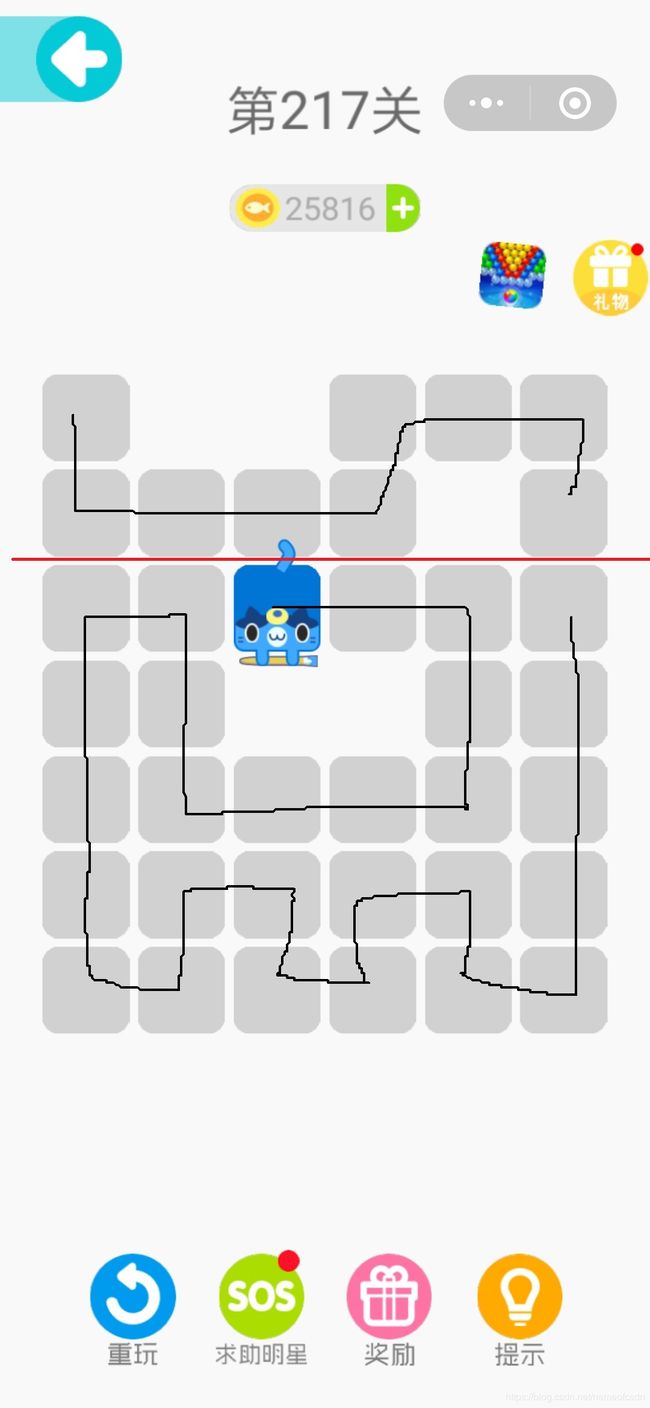
比如第217关:
终点在左上角,如果切除左边2列,很容易得到:
如果切除上面2行,也很容易得到:
实际上,这个规律可以拓展成一般规律:
绝大部分关卡都存在这样的一个解:存在某条平行于坐标轴的直线把路径分为两部分,整条路径只跨越这条直线一次,即这条直线刚好把路径分为左右两块或上下两块。
从217关往后就再也没有什么新发现了,基本上都是一样的,下面列出我玩过的所有关卡极其答案: