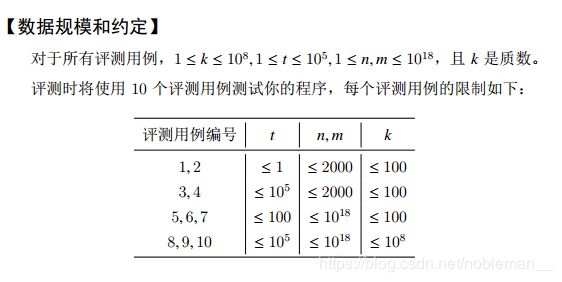
2019 第十届蓝桥杯大赛软件类省赛 C/C++ 大学 A 组 【部分题解】

声明： 这些的答案不是官方答案，都是我自己做的，仅供参考。一起加油

试题 A: 平方和

本题总分：$5^{\prime }$
【问题描述】

小明对数位中含有 $2、0、1、9$ 的数字很感兴趣，在$1$ 到 $40$ 中这样的数包括 $1、2、9、10$ 至 $32、39$ 和$40$，共 $28$ 个，他们的和是 $574$，平方和是 $14362$。注意，平方和是指将每个数分别平方后求和。
请问，在 $1$ 到 $2019$ 中，所有这样的数的平方和是多少？

分析：

无

本题答案：2658417853

参考代码

#include 

using namespace std;
typedef long long ll;

ll sum = 0;

bool f(int x) {
    while (x) {
        int t = x % 10;
        x /= 10;
        if (t == 2 || t == 0 || t == 1 || t == 9) 
        	return true;
    }
    return false;
}

/// 2658417853

int main() {
    for (int i = 1; i <= 2019; i++) {
        if (f(i)) sum += i *  1ll * i;
    }
    cout << sum <<endl;
    return 0;
}

试题 B: 数列求值

本题总分： $5^{\prime }$
【问题描述】
给定数列 $1,1,1,3,5,9,17,\dots$，从第 $4$ 项开始，每项都是前 $3$ 项的和。求第 $20190324$ 项的最后 $4$ 位数字。

分析：

直接递推，不需要那么大的数组，只要求最后四位数，每次同余即可

本题答案：4659

参考代码

#include 

using namespace std;

int a[4] = {1,1,1};

/// 4659

int main() {
    for (int i = 0; i < 20190324 - 3; i++) {
        int s = a[0] + a[1] + a[2];
        s %= 10000;
        a[0] = a[1];
        a[1] = a[2];
        a[2] = s;
    }
    cout << a[2] << endl;
    return 0;
}

试题 C: 最大降雨量

本题总分： $10^{\prime }$

【问题描述】

由于沙之国长年干旱，法师小明准备施展自己的一个神秘法术来求雨。这个法术需要用到他手中的 $49$ 张法术符，上面分别写着 $1$ 至 $49$ 这 $49$ 个数字。法术一共持续 $7$ 周，每天小明都要使用一张法术符，法术符不能重复使
用。每周，小明施展法术产生的能量为这周 $7$ 张法术符上数字的中位数。法术施展完 $7$ 周后，求雨将获得成功，降雨量为 $7$ 周能量的中位数。由于干旱太久，小明希望这次求雨的降雨量尽可能大，请大最大值是多少？

分析：

贪心的来放就行，我们的第一感觉应该就是第一周放$1-7$,第二周放$8-14$，……，第七周放 $43-49$。这样的话我们发现最大值取决于第四周的中位数，和其他周的没关系，又可以发现，第$5，6，7$周只需要保证每周的中位数大于第$4$周的中位数即可，我们可以采用下面的方案。（见下图）

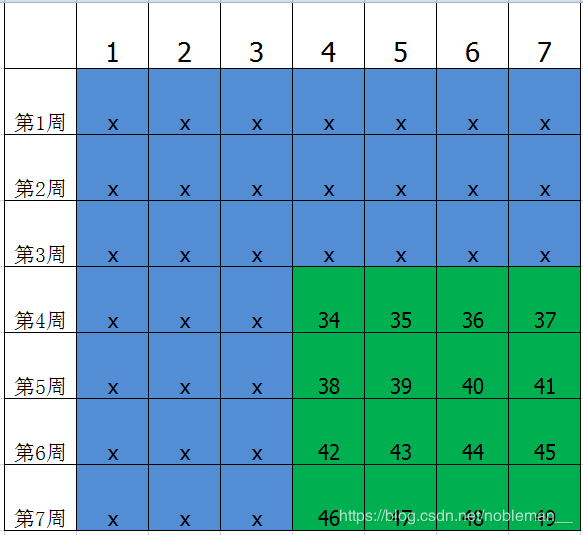
只需要保证绿色部分按照方案中的放，其他的随便放即可，都不会影响答案

所以这题答案为： $34$

试题 D: 迷宫

本题总分： $10^{\prime }$
【问题描述】
下图给出了一个迷宫的平面图，其中标记为 $1$ 的为障碍，标记为 $0$ 的为可以通行的地方。

010000
000100
001001
110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。
对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫，一共 10 步。其中D、 U、 L、 R 分别表示向下、向上、向左、向右走。对于下面这个更复杂的迷宫（30 行 50列），请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。请注意在字典序中D。（如果你把以下文字复制到文本文件中，请务
必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt(如下），内容与下面的文本相同）

01010101001011001001010110010110100100001000101010
00001000100000101010010000100000001001100110100101
01111011010010001000001101001011100011000000010000
01000000001010100011010000101000001010101011001011
00011111000000101000010010100010100000101100000000
11001000110101000010101100011010011010101011110111
00011011010101001001001010000001000101001110000000
10100000101000100110101010111110011000010000111010
00111000001010100001100010000001000101001100001001
11000110100001110010001001010101010101010001101000
00010000100100000101001010101110100010101010000101
11100100101001001000010000010101010100100100010100
00000010000000101011001111010001100000101010100011
10101010011100001000011000010110011110110100001000
10101010100001101010100101000010100000111011101001
10000000101100010000101100101101001011100000000100
10101001000000010100100001000100000100011110101001
00101001010101101001010100011010101101110000110101
11001010000100001100000010100101000001000111000010
00001000110000110101101000000100101001001000011101
10100101000101000000001110110010110101101010100001
00101000010000110101010000100010001001000100010101
10100001000110010001000010101001010101011111010010
00000100101000000110010100101001000001000000000010
11010000001001110111001001000011101001011011101000
00000110100010001000100000001000011101000000110011
10101000101000100010001111100010101001010000001000
10000010100101001010110000000100101010001011101000
00111100001000010000000110111000000001000000001011
10000001100111010111010001000110111010101101111000

分析：

这题没的说，典型的bfs，记录路径，在查找的时候按照题目要求的进行查找（先下，在左…）,还有就是在保存路径的时候还要记录下本次是往那个反向走的，这个参数。还有这个读入文件有点坑，建议采用文件的方式读入读出。

本地答案如下(仅供参考）：DDDDRRURRRRRRDRRRRDDDLDDRDDDDDDDDDDDDRDDRRRURRUURRDDDDRDRRRRRRDRRURRDDDRRRRUURUUUUUUULULLUUUURRRRUULLLUUUULLUUULUURRURRURURRRDDRRRRRDDRRDDLLLDDRRDDRDDLDDDLLDDLLLDLDDDLDDRRRRRRRRRDDDDDDRR

参考代码

#include 

using namespace std;
const int maxn = 1e2 + 10;
typedef long long ll;

#define fi first
#define se second
#define pii pair

char mp[maxn][maxn];
int vis[maxn][maxn];
pair<pii, char> pre[maxn][maxn];

/// D < L < R < U
string ss = "DLRU";
int Move[4][2] = {1,0,  0,-1,  0,1,  -1,0};
int n = 30, m = 50;

void bfs() {
    queue<pii> q;
    q.push(pii(0,0));
    vis[0][0] = 1;
    pre[0][0] = make_pair(pii(-1,-1), ' ');
    while (!q.empty()) {
        pii u = q.front(); q.pop();
        int x = u.fi, y = u.se;
        for (int i = 0; i < 4; i++) {
            int tox = x + Move[i][0];
            int toy = y + Move[i][1];
            if (tox < 0 || tox >= n || toy < 0
                || toy >= m || vis[tox][toy] ||
            mp[tox][toy] == '1') {
                continue;
            }
            vis[tox][toy] = 1;
            pre[tox][toy] = make_pair(u, ss[i]);
            q.push(pii(tox, toy));
        }

    }
}

void print(int x, int y) {
    if (x == -1 && y == -1) {
        return ;
    }
    print(pre[x][y].fi.fi, pre[x][y].fi.se);
    cout << pre[x][y].se;
}

int main() {
    freopen("C:\\Users\\Administrator\\Desktop\\in.txt", "r", stdin);
    freopen("C:\\Users\\Administrator\\Desktop\\out.txt", "w", stdout);
    for (int i = 0; i < n; i++) {
        scanf("%s", mp[i]);
    }
    bfs();
    print(29,49);
    return 0;
}

试题 E: RSA 解密

本题总分： $15^{\prime }$
【问题描述】
RSA 是一种经典的加密算法。它的基本加密过程如下。
首先生成两个质数 $p,q，令n=p\cdot q，设d与(p-1)\cdot (q-1)$ 互质，则可找到 $e$ 使得 $d\cdot e除(p-1)\cdot (q-1)的余数为1$。$n,d,e组成了私钥，n,d$组成了公钥。当使用公钥加密一个整数 $X时（小于n），计算C=X^{d}modn，则C$ 是加密后的密文。当收到密文 C 时，可使用私钥解开，
计算公式为 $X=C^{e}modn。$

例如，当 $p=5,q=11,d=3时，n=55,e=27$。
若加密数字 $24，得243mod55=19$。
解密数字 $19，得1927mod55=24$。

现在你知道公钥中 $n=1001733993063167141,d=212353，同时你截获了别人发送的密文C=20190324$，请问，原文是多少？

分析：

这题算有点坑吧，题意也不难读懂，已知$n,d,C,求X，欲求X，需求e，欲求e，需求两个质数p,q，其实不难求，当时比赛的时候为求稳点，用了Java的大数类，用c++的快速幂也可以，这里Java的仅供参考。我是一开始暴力求的两个质数p,q,p=891234941,q=1123984201;接下来就是很裸的Java大数了。$

PS：这题SB了，犯了超低级的错误，计算x的时候d和e弄混了，少了15分，这下彻底进不了国赛了-_- !

本题答案(仅供参考）：x = 579706994112328949（已更正）

import java.math.BigInteger;

public class Main {
    /**
     * @param args
     */
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        BigInteger p = BigInteger.valueOf(891234941);
        BigInteger q = BigInteger.valueOf(1123984201);
        BigInteger n = q.multiply(p);
        System.out.println(n);
        BigInteger p_1 = p.subtract(BigInteger.ONE);
        BigInteger q_1 = q.subtract(BigInteger.ONE);
        BigInteger w = p_1.multiply(q_1);

        BigInteger c = BigInteger.valueOf(20190324);
        BigInteger d = BigInteger.valueOf(212353);

        for (int i = 2; i < 1000000; i++) {
            BigInteger s = w.multiply(BigInteger.valueOf(i)).add(BigInteger.valueOf(1));
            if (s.mod(d).equals(BigInteger.valueOf(0))) {
                BigInteger e = s.divide(d);
                System.out.println("e = " + e);
                BigInteger x = c.modPow(e, n);
                System.out.println("x = " + x);
                BigInteger isc = x.modPow(d,n);
                System.out.println(isc);
                break;
            }
        }
    }

}

试题 F: 完全二叉树的权值

时间限制: 1.0s 内存限制: 256.0MB

本题总分： $15^{\prime }$

【问题描述】

给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1, A2, · · · AN，如下图所示：

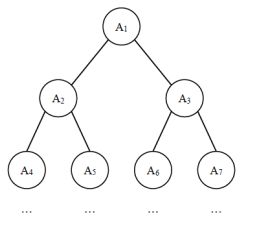
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？如果有多个深度的权值和同为最大，请你输出其中最小的深度。
注：根的深度是 1。

【输入格式】

第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · AN 。

【输出格式】

输出一个整数代表答案。

【样例输入】

7
1 6 5 4 3 2 1

【样例输出】

2

【评测用例规模与约定】

对于所有评测用例， 1 ≤ N ≤ 100000， −100000 ≤ Ai ≤ 100000。

分析 :

最基本的树的题了把，题目上已经给出了是完全二叉树，所以直接用数组来模拟方便些，用两个队列来模拟即可，每次记录下层数，看范围可知，答案会爆int，这里要开longlong。

参考代码

#include 

using namespace std;
typedef long long ll;

ll t[maxn];
queue<int> q1, q2;

int main() {
    int n; cin >> n;
    for (int i = 1; i <= n; i++) cin >> t[i];
    ll res = 1;
    ll ma = t[1];
    q1.push(1);
    int c = 0;
    while (q1.size()) {
        ll s = 0;
        c++;
        while (q1.size()) {
            int now = q1.front(); q1.pop();
            s += t[now];
            if (now * 2 <= n) {
                ll t1 = now * 2, t2 = now * 2 + 1;
                q2.push(t1);
                q2.push(t2);
            }
        }
        if (s > ma) {
            ma = s;
            res = c;
        }
        while (q2.size()) {
            q1.push(q2.front());
            q2.pop();
        }
    }
    cout << res << endl;
    return 0;
}

试题 G: 外卖店优先级

时间限制: 1.0s 内存限制: 256.0MB
本题总分： $20^{\prime }$

【问题描述】

“饱了么”外卖系统中维护着 N 家外卖店，编号 1 ∼ N。每家外卖店都有一个优先级，初始时 (0 时刻) 优先级都为 0。
每经过 1 个时间单位，如果外卖店没有订单，则优先级会减少 1，最低减到 0；而如果外卖店有订单，则优先级不减反加，每有一单优先级加 2。如果某家外卖店某时刻优先级大于 5，则会被系统加入优先缓存中；如果优先级小于等于 3，则会被清除出优先缓存。给定 T 时刻以内的 M 条订单信息，请你计算 T 时刻时有多少外卖店在优先缓存中。

【输入格式】

第一行包含 3 个整数 N、 M 和 T。
以下 M 行每行包含两个整数 ts 和 id，表示 ts 时刻编号 id 的外卖店收到
一个订单。

【输出格式】

输出一个整数代表答案。

【样例输入】

2 6 6
1 1
5 2
3 1
6 2
2 1
6 2

【样例输出】

1

【样例解释】

6 时刻时， 1 号店优先级降到 3，被移除出优先缓存； 2 号店优先级升到 6，加入优先缓存。所以是有 1 家店 (2 号) 在优先缓存中。

【评测用例规模与约定】

对于 80% 的评测用例， 1 ≤ N; M; T ≤ 10000。
对于所有评测用例， 1 ≤ N; M; T ≤ 100000， 1 ≤ ts ≤ T， 1 ≤ id ≤ N。.

分析：

分值都到20了，有点难度了，我们可以暴力的模拟时间轴，每个都更新来做，不过应该最多30分吧。
我的做法是用一个数组d 来记录 当前店的优先级，以及最后修改的时间，然后每次O(1)的修改，也就是说当有一个订单来的时候，我们才对这个这个订单修改相关的信息即可，不过要求所有的订单要根据时间的顺序来请求，每次请求时，判断当前外卖店的优先级，和最后的修改的时间，我们还需要记录优先缓存中的数量，这里注意：要在最后再来扫一遍，来更新所有店的状态。这里具体解释下样例。

首先对样例进行排序后为
$时间店家当前优先级最后修改时间$
$1121$
$2142$
$316（加入缓存区）3$
$5225$
$6246$
$626（加入缓存区）6$

最后扫一遍，发现1店，不满足，移除缓存区，具体看代码

参考代码

#include 

using namespace std;
const int maxn = 1e5 + 10;
typedef long long ll;

#define pii pair

int f[maxn];
int d[maxn][3];
vector<pii> a;
int r; /// 缓冲区的个数

int main() {
    int n, m, k; cin >> n >> m >> k;
    for (int i = 0; i < m; i++) {
        int x, y; cin >> x >> y;
        a.push_back(pii(x, y));
    }
    sort(a.begin(), a.end());
    for (int i = 0; i < m; i++) {
        int now = a[i].fi;
        int w = a[i].se;
        if (now > k) break;
        if (d[w][0] == 0) { /// 特判下之前没有接到过订单
            d[w][0] = 2;
            d[w][1] = now;
        } else {
            /// 注意特判修改时间相同时
            if (d[w][1] != now)   d[w][0] -= (now - d[w][1] - 1);
            if (d[w][0] < 0) d[w][0] = 0;
            d[w][0] += 2;
            d[w][1] = now;
            if (d[w][0] > 5 && !f[w]) {
                r++;
                f[w] = 1;
            }
            if (f[w] && d[w][0] <= 3) {
                f[w] = 0; r--;
            }
        }
    }
    for (int i = 1; i <= n; i++) {
        if (d[i][0]) {
            d[i][0] -= (k - d[i][1]);
            if (d[i][0] < 0) d[i][0] = 0;
            if (d[i][0] > 5 && !f[i]) {
                r++;
                f[i] = 1;
            }
            if (f[i] && d[i][0] <= 3) {
                f[i] = 0; r--;
            }
        }
    }
    cout << r << endl;
    return 0;
}

试题 H: 修改数组

时间限制: 1.0s 内存限制: 256.0MB
本题总分： $20^{\prime }$

【问题描述】

给定一个长度为 N 的数组 A = [A1; A2; · · · AN]，数组中有可能有重复出现的整数。
现在小明要按以下方法将其修改为没有重复整数的数组。
小明会依次修改A2; A3; · · · ; AN。当修改 Ai 时，小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过，则小明会给 Ai 加上 1 ；如果新的 Ai 仍在之前出现过，小明会持续给 Ai 加 1 ，直到 Ai 没有在 A1 ∼ Ai−1 中出现过。当 AN 也经过上述修改之后，显然 A 数组中就没有重复的整数了。
现在给定初始的 A 数组，请你计算出最终的 A 数组。

【输入格式】

第一行包含一个整数 N。
第二行包含 N 个整数 A1; A2; · · · ; AN 。

【输出格式】

输出 N 个整数，依次是最终的 A1; A2; · · · ; AN。

【样例输入】

5
2 1 1 3 4

【样例输出】

2 1 3 4 5

【评测用例规模与约定】
对于 80% 的评测用例， 1 ≤ N ≤ 10000。
对于所有评测用例， 1 ≤ N ≤ 100000， 1 ≤ Ai ≤ 1000000。

分析：

这题一开始看错了，在最后压线交的，不知道对不对，应该不对–

我思路是：因为范围是1e6,直接开个数组x 来表示当前位置的下一个空闲的位置。当一个Ai到来的时候，如果没出现过，既x[Ai]为0时，我们直接把Ai放在该位置，然后求得下一个空闲的位置，由于还要考虑当前位置已经放过的时候，所以我们把获取下一个位置写作一个函数，当Ai位置出现过，我们把Ai放在x[Ai]处，既下一个空闲的位置上，然后更新下放完后Ai位置的下一个空闲的位置。
我们考虑怎么写更新当前位置的下一个空闲位置的函数
假设正在考虑n位置
如果n-1位置访问过，那么我们还要考虑n+1是否访问过，如果都访问过（如下）

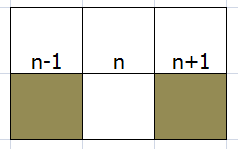
我们要更新n-1以及n的位置，而n+1的位置不用更新

当n-1位置访问过，n+1没有访问过（如下）

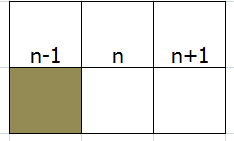
我们同样更新 n -1的位置和n的位置

当n-1位置没有访问过，n+1位置访问过

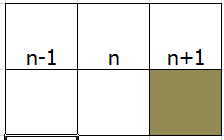
我们只需要更新n位置即可

最后一种情况就是两边都没有访问过。

参考代码

#include 

using namespace std;
const int maxn = 1e6 + 10;

int x[maxn];
vector<int> r;

int f(int n) {
    if (x[n - 1]) {
        if (x[n + 1]) {
            x[n - 1] = x[n] = x[n + 1];
        } else {
            x[n - 1] = x[n] = n + 1;
        }
    } else {
        if (x[n + 1]) {
            x[n] = x[n + 1];
        } else {
            x[n] = n + 1;
        }
    }
    return x[n];
}

int main() {
    int n; cin >>n;
    for (int i = 0; i < n; i++) {
        int s; cin >> s;
        if (x[s]) {
            int to = x[s];
            r.push_back(to);
            x[to] = f(to);
        } else {
            x[s] = f(s);
            r.push_back(s);
        }
    }

    for (int i = 0; i < r.size(); i++) {
        if (i != 0) cout << ' ';
        cout << r[i];
    }
    cout << endl;
    
    return 0;
}

试题 I: 糖果

时间限制: 1.0s 内存限制: 256.0MB
本题总分： $25^{\prime }$

【问题描述】

糖果店的老板一共有 M 种口味的糖果出售。为了方便描述，我们将 M 种口味编号 1 ∼ M。小明希望能品尝到所有口味的糖果。遗憾的是老板并不单独出售糖果，而是 K 颗一包整包出售。
幸好糖果包装上注明了其中 K 颗糖果的口味，所以小明可以在买之前就知道每包内的糖果口味。
给定 N 包糖果，请你计算小明最少买几包，就可以品尝到所有口味的糖果。

【输入格式】

第一行包含三个整数 N、 M 和 K。
接下来 N 行每行 K 这整数 T1; T2; · · · ; TK，代表一包糖果的口味。
【输出格式】
一个整数表示答案。如果小明无法品尝所有口味，输出 −1。

【样例输入】

6 5 3
1 1 2
1 2 3
1 1 3
2 3 5
5 4 2
5 1 2

【样例输出】

2

【评测用例规模与约定】

对于 30% 的评测用例， 1 ≤ N ≤ 20 。
对于所有评测样例， 1 ≤ N ≤ 100， 1 ≤ M ≤ 20， 1 ≤ K ≤ 20， 1 ≤ Ti ≤ M。

分析：

不愧是25分的题，不会做，只会暴力，应该能过30的数据，有大佬会，给小弟留言呗~~xiexie

参考代码

#include 

using namespace std;
const int maxn = 1e2 + 10;

int a[maxn][maxn];

int main() {
    int n,m,k; cin >> n >> m >> k;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < k; j++) {
            cin >> a[i][j];
        }
    }
    int mi = 10000000;
    for (int i = 1; i < (1 << n); i++) {
        int t = 0;
        int cnt = 0;
        for (int j = 0; j < n; j++) {
            if (i & (1 << j)) {
                cnt++;
                for (int x = 0; x < k; x++) {
                    t |= (1 << (a[j][x] - 1));
                }
            }
        }
        if (t == ((1 << m) - 1)) {
            mi = min(mi, cnt);
        }
    }
    if (mi == 10000000) mi = -1;
    cout << mi << endl;
    return 0;
}

试题 J: 组合数问题

时间限制: 1.0s 内存限制: 256.0MB
本题总分： $25^{\prime }$

【问题描述】

给 $n;m;k$，求有多少对 $(i;j)$ 满足 $1\le i\le n;0\le j\le min(i;m)且C_i^j\equiv 0(modk)$， $k是质数。其中C_i^j是组合数，表示从i个不同的数中选出j个组成$一个集合的方案数。

【输入格式】

第一行两个数 t; k，其中 t 代表该测试点包含 t 组询问， k 的意思与上文中相同。接下来 t 行每行两个整数 n; m，表示一组询问。

【输出格式】

输出 t 行，每行一个整数表示对应的答案。由于答案可能很大，请输出答
案除以 109 + 7 的余数。

【样例输入】

1 2
3 3

【样例输出】

1

【样例说明】

在所有可能的情况中，只有 $C_2^1=2是2的倍数$。

【样例输入】

2 5
4 5
6 7

【样例输出】

0
7

【样例输入】

3 23
23333333 23333333
233333333 233333333
2333333333 2333333333

【样例输出】

851883128
959557926
680723120

分析：

不会，本来还想暴力的打个表，混两个点的数据，后来检查了一遍，也没写。真难…

总结：

这是我第二次参加蓝桥杯了，去年参加的B组的c++，最后水个省一，国二，由于去年的下半年一直在准备考研，一直都以为这次的比赛被复试耽误了，最后还是参加上了，总的来说感觉今年的A组的题和去年B组难度差不多，最后两个题是真的难，之前我还是有点依赖板子，比如数论相关的题，都是靠板子来打比赛，也是我好久没敲过代码了，中间挺了快大半年，思路都跟不上，还好出错，一个bug找一个小时，还是太菜了，感觉这次最多也是个省二啦，重在参与，还是得认真codeing~~