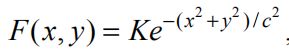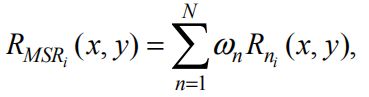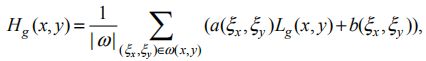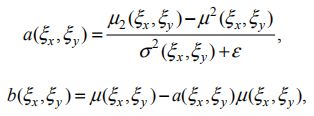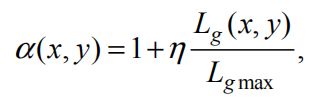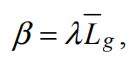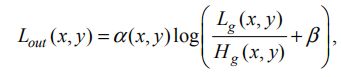一种基于视神经网络的高动态范围（HDR）图像自适应局部色调映射的实现【OpenCV】【CUDA】

 

原理是基于这篇论文——《Adaptive Local Tone Mapping Based on Retinex for High Dynamic Range Images》

论文提出的背景

虽然可以从不同曝光的照片中获得包含真实场景全动态范围的高动态范围 (HDR) 图像，但是普通显示器等低动态范围(LDR)显示设备无法处理场景的全动态范围。LDR 设备只能显示两个数量级的。一旦将 HDR 图像线性映射到显示设备，就会丢失很多信息。因此，在映射到设备之前，必须对 HDR 图像进行压缩。从 HDR 图像到 LDR 显示设备的映射技术称为色调映射或色调再现。

这些色调映射技术可以分为两类：第一类是全局操作符，另一类是局部操作符。

1. 全局色调映射操作符是对所有像素应用一个函数；
2. 局部色调映射算子根据相邻像素对每个像素应用不同的函数。

什么是中心环绕视网膜

retinex 理论最初是由 Land 定义的。说明了人类视觉系统如何提取世界上可靠的颜色信息。Jobson 等人在中心/环绕视网膜的基础上，引入了单尺度视网膜 (SSR) 和多尺度视网膜 (MSR) 。

SSR 的公式 

其中 x,y 为图像像素坐标， 为视网膜输出， 为图像在第 i 个光谱波段的分布，*为卷积运算，F(x,y) 为高斯环绕函数

 其中 c 是高斯环绕空间常数。K 是归一化因子（一个小的空间常数会产生良好的动态范围压缩，但颜色再现却比较糟糕。相反，一个大的常数能产生良好的颜色再现，但动态范围压缩却不太好）。

MSR 的公式

其中 N 是尺度的数量,  表示第 n 个尺度的第 i 个组成部分， 是 MSR 输出的第 i 个光谱分量， 是与第 n  个尺度相关的权重。 

MSR 的目标是减少高对比度边缘周围的晕圈伪影，并与动态范围压缩和颜色再现保持平衡。MSR 产生了良好的动态范围压缩，但仍然遭受光晕伪影的影响。此外，小空间常数的 SSR 使图像中较大的均匀区域变灰变平。

如图所示，

                                                      左图是 MSR 的输出，右图是带小空间常量的 SSR  的输出

作者提出的算法

为了解决以上的缺陷，Hyunchan Ahn 等人提出了一种新的局部色调映射方法，该方法基于中心/环绕视网膜，既能保留细节，又能防止光晕产生。

在算法中，亮度值从输入的 HDR 图像中获得并处理。首先，应用全局色调映射作为预处理。在此基础上，应用了基于视网膜算法的局部色调映射。最后，对处理后的亮度值和输入的色度值进行归一化，得到输出图像。

全局色调映射

原理不复杂，这篇博客已经详细阐述了——https://blog.csdn.net/just_sort/article/details/84030723#commentsedit，我就不再赘述。

根据博主的朴素实现（但是博主只实现了全局自适应部分的代码，局部自适应并没有实现）

我优化的 OpenCV 代码如下：

int HDR(const cv::Mat &input_img, cv::Mat &out_img)
{
    int rows = input_img.rows;
    int cols = input_img.cols;

    cv::Mat src;
    input_img.convertTo(src, CV_32FC3);

    // -----------------------------------------------------------------------
    //Timer t;

    //Lw_max
    float Lw_max = 0.0;

    //Lw
    cv::Mat Lw = cv::Mat(rows, cols, CV_32FC1, cv::Scalar(0));

    for (int i = 0; i < rows; i++)
    {
        cv::Vec3f *ptr_vec3 = src.ptr(i);
        float *ptr = Lw.ptr(i);

        for (int j = 0; j < cols; j++)
        {
            float tmp_0 = 0.299f * ptr_vec3[j][2];
            float tmp_1 = 0.587f * ptr_vec3[j][1];
            float tmp_2 = 0.114f * ptr_vec3[j][0];

            float val = tmp_0 + tmp_1 + tmp_2;

#if 1
            if (fabs(val) < 1e-5)
            {
                ptr[j] = 1;
            }
            else
            {
                ptr[j] = val;
            }
#else
            Lw.ptr(i)[j] = val == 0 ? 1 : val;
#endif

            Lw_max = max(val, Lw_max); // 公式 4 中的 Lw_max
        }
    }
    //std::cout << "Lw_max; " << t.elapsed() << std::endl;

    // -----------------------------------------------------------------------

    //t.restart();
    // Lw_sum
    float Lw_sum = 0;
    for (int i = 0; i < rows; i++)
    {
        float *ptr = Lw.ptr(i);
        for (int j = 0; j < cols; j++)
        {
            // .001f 其作用主要是为了避免对纯黑色像素进行 log 计算时数值溢出
            float val = log(0.001f + ptr[j]);
            Lw_sum += val; // 公式 5 的求和部分
        }
    }

    //std::cout << "sum; " << t.elapsed() << std::endl;

    // -----------------------------------------------------------------------

    //t.restart();
    // Lwaver 公式 5 的倒数
    float inv_Lwaver = 1.f  / exp(Lw_sum / (rows * cols));

    for (int i = 0; i < rows; i++)
    {
        float *ptr = Lw.ptr(i);
        cv::Vec3f *ptr_vec3 = src.ptr(i);

        //#pragma omp parallel for schedule (dynamic)
        for (int j = 0; j < cols; j++)
        {
            float val = ptr[j];
            float top = log(val * inv_Lwaver + 1);
            float bottom = log(Lw_max * inv_Lwaver + 1);
            float Lg = top / bottom;

            // 低照度的亮度部分比高照度的部分要能得到更大程度的提升，所以对于低照度图，该公式能起到很好的增强作用
            // 式中使用了全局的对数平均值，这就有了一定的自适应性。
            float gain = Lg / val;

            ptr_vec3[j][0] *= gain;
            ptr_vec3[j][1] *= gain;
            ptr_vec3[j][2] *= gain;
        }

    }
    //std::cout << "公式 5; " << t.elapsed() << std::endl;

    src.convertTo(out_img, CV_8UC3, 255.f);

    return 0;
}

执行的效果为（图片大小为 894*1080，屏幕大小有限，截图只截取了一部分）：

OpenCV 的版本执行（100次）时间平均为 48.14ms 左右 

经过 CUDA 优化之后的效果基本一致

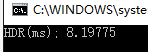
 但是执行时间大大减少，减少为仅需 8.2 ms（执行 100 次，取平均，包括 host 和 device 之间的拷贝时间）

 其他图片（也放缩成高度为 1080，宽度保持纵横比）效果：

7.55 ms

10.80 ms

基于视网膜算法的局部色调映射

基于视网膜理论的局部适应是在全局适应过程之后进行的。作者发现位于亮得多的像素值附近的输入 的输出 会变得非常暗，这将导致光晕伪影，使结果看起来不自然。通过引入边缘保持滤波器，可以减少伪影。因此作者采用导向滤波器代替高斯滤波器。导向滤波器是一种与双边滤波器类似的保边滤波器，其权值不仅取决于欧几里德距离，还取决于亮度差。这些滤波器的性能相似，但导向滤波器在边缘附近有更好的性能。此外，它的计算复杂度是线性时间的，没有近似，与核大小无关。

局部适应方程可表示为

式中， 为局部自适应的输出， 为导向滤波器对 的输出，

邻域像素坐标, 是一个（以像素为 (x, y) 中心，以 r 为半径的）局部方形窗口，|ω| 是在 内像素的数量 ) 和 是一些线性系数。

  和 分别是 在 窗口下的 的均值和方差， 是 在 窗口下的均值，ε 是正则化参数。【因为在作者的算法中传进导向滤波器的导向图像与输入图像是一致的，所以公式看起来和何凯明的原公式有点不太一样，其实是一致的】

应用该滤波器后，光晕伪影明显减少，但由于其全局对比度较低，输出的整体外观仍然令人不够满意。

为了防止滤波产生的平面现象，提高我们的方法的性能，作者引入了两个重要因素。

①、对比度增强因子 α

②、根据场景内容变化的自适应非线性偏移量 β

 其中 η 表示对比控制参数， 是全局自适应输出的最大亮度值。

其中 λ 是非线性控制参数, 是全局自适应输出的亮度对数均值。

最后得到局部自适应的公式为：

最终的效果

 先经过全局自适应，再经过局部自适应后的结果如下所示