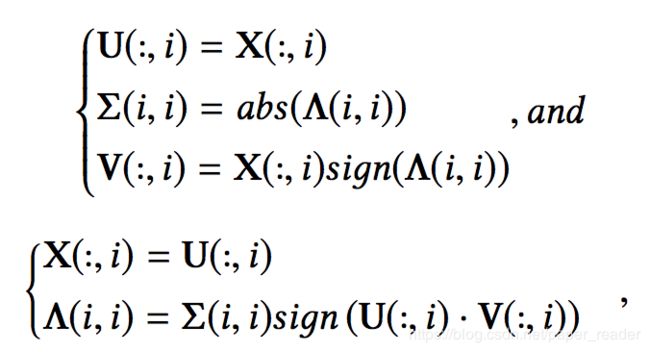KDD18': 捕捉网络中任一阶邻近度的 Network Embedding
KDD18': 捕捉网络中任一阶邻近度的 Network Embedding
给定一个图G=
传统算法是将Network Embedding问题看做矩阵分解或矩阵降维问题，对图的邻接矩阵应用矩阵分解或奇异值分解等方法进行降维，这样做的好处是可以很容易地通过学习出的embedding vector复原出原有的图结构。然而这样做的缺点也很明显，仅仅对邻接矩阵进行降维，就是只考虑直接邻居对当前节点的影响，忽视了图中2度，3度乃至更远的节点对当前节点的影响。
在此之后，随着深度学习的发展，产生了基于随机游走（random walk）算法的深度学习Network Embedding框架：DeepWalk, Line, node2vec。它们的主要原理都很简单：通过随机游走在图中进行采样，再通过采集到的序列数据学习网络中节点的表达。这样的做法最大的好处是能够考虑到较远的节点对当前节点产生的影响。然而随机游走算法有着很大的不确定性，往往要在算法的精度和运行时间之间做牺牲。
KDD18 的这篇文章 Arbitrary-Order Proximity Preserved Network Embedding 拓展了传 统的基于矩阵降维的embedding算法，在保证高精度的同时也能在线性时间下运行，取得了不错的效果。
算法首先定义了高阶邻近度的概念：
S=F(A)=w1A+ w1A2+ w1A3+ w1A4+ w1A5…
其中A是无向图的邻接矩阵。我们知道，如果A是邻接矩阵的话，其中的每个数字都是两个相邻的点之间的权重（如果这两点之间有边连接的话）。进一步地，A2，A3，A4……中的每一个数字代表的就是两个点之间通过2段边，3段边，4段边……互相连接的权重。所以，矩阵S就是包含了多种邻近度的图的加权和，相比较邻接矩阵A而言，更能表达图中的点与点关联的程度。
所以，只要对矩阵S进行分解，分解到的结果U*就是我们所求的Node Embedding向量。
min||S-U* V*T||F2
高秩矩阵的矩阵分解，一般可以由SVD的结果从高处截断得到：
如果S=UΣV（SVD结果），只截取SVD结果中奇异值最高的一部分的话，那么U* =U√Σ,V* =V√Σ。其中U* V*是矩阵分解的结果，UΣV三个矩阵是SVD的结果。
进一步地，SVD的结果又可以通过特征值分解的结果得到（X和Λ分布是特征向量和特征值）：
所以，只要计算出矩阵S的特征值和特征向量，就相当于得到了S的矩阵分解结果，进一步就得到了含有高阶邻近度信息的Node Embedding。文献Richard B Lehoucq and Danny C Sorensen. 1996. De ation techniques for an implicitly restarted Arnoldi iteration. SIAM J. Matrix Anal. Appl. (1996). 给出了计算特征值和特征向量的一种快速算法，计算最大的几个特征值和对应的特征向量只需要O(T(Nl2 + Ml) ,其中N和M分别是节点和边的数量，l是计算前top-l大的特征值和特征向量，T是算法迭代的次数。
然而先通过S=F(A)=w1A+ w1A2+ w1A3+ w1A4+ w1A5…计算S，再通过上述方法计算特征值和特征向量，计算量实在太大。如果先对邻接矩阵A计算特征值和特征向量，再对得到的Node Embedding Vector 上应用函数F呢？文章后文提出两个定理，证明这样操作的正确性和合理性。
定理一：如果λ和x是矩阵A的一组特征值和特征向量，那么F(λ)和x依然是S的一组特征值和特征向量。
这个定理很容易证明，因为求特征值和特征向量是线性代数操作，F是乘法和加法的组合，所以特征值和特征向量与矩阵的对应关系很容易对函数F保持恒定。
定理二：如果λ和x是矩阵A的特征值和特征向量，显然F(λ)和x依然是S的一组特征值和特征向量，而如果F(λ)和x在S上的排名不超过d的话，那么λ和x在矩阵A上的排名不超过l。其中l的取值方法是：在矩阵A上，排名前l的特征值中有超过d个正值。
这样说起来有点拗口，但实验中l往往小于2d。
证明方法如下：假设λi和λj分别是A的两个特征值且|λi|>|λj|, λi>0.
那么
所以，只要A的top-l的特征值中有d个大于0的，那么在计算F(λ)后，就依然会有d个特征值排在前面。
这样看来，只要针对邻接矩阵A计算特征值和特征向量，再针对特征值应用函数F(x)= w1x+ w1x2+ w1x3+ w1x4+ w1x5…,
就能得到embedding vector了。具体算法如下：
算法复杂度是O(T(Nl2 +Ml)+r(l +Nd)) , 其中N和M分别是节点和边的数量，l是计算前top-l大的特征值和特征向量，T是特征值算法迭代的次数。因此该算法针对N和M均为线性的。
该算法在link prediction，reconstruction等任务上均取得了优于baseline（DeepWalk, Line, node2vec）的结果。但是该算法也有它的缺点，比如无法利用side information，只能在无向图上计算等缺点。