LeetCode(4)-链表:快慢指针

文章目录

• • • LeetCode 876.链表的中间节点
    • LeetCode 19. 删除链表的倒数第N个节点
    • LeetCode 141. 环形链表

 

链表中有一个很常用的技巧被称为快慢指针技巧,通常用于找到中间节点和用于解决一些具有环状链表性质的问题

LeetCode 876.链表的中间节点

给定一个带有头结点 head 的非空单链表，返回链表的中间结点。
如果有两个中间结点，则返回第二个中间结点。
示例 1：
输入：[1,2,3,4,5]
输出：此列表中的结点 3 (序列化形式：[3,4,5])
返回的结点值为 3 。 (测评系统对该结点序列化表述是 [3,4,5])。
注意，我们返回了一个 ListNode 类型的对象 ans，这样：
ans.val = 3, ans.next.val = 4, ans.next.next.val = 5, 以及 ans.next.next.next = NULL.
示例 2：
输入：[1,2,3,4,5,6]
输出：此列表中的结点 4 (序列化形式：[4,5,6])
由于该列表有两个中间结点，值分别为 3 和 4，我们返回第二个结点。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/middle-of-the-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

其实这个问题有两种解法,一种是使用快慢指针,另一种比较容易想到的是使用计数法,先说说用计数法如何解决这个问题:

首先遍历一遍链表,确定链表长度len,在下一个循环中定义迭代len / 2 次即可找到中间节点了:

代码实现:

public ListNode middleNode(ListNode head) {
        if (head == null) return null;
        int len = 0;
        ListNode counter = head;
        while (counter != null) {
            len++;
            counter = counter.next;
        }
        System.out.println(len);
        for (int i = 0; i < len / 2; i++) {
            head = head.next;
        }
        return head;
    }

使用计数法需要遍历一次链表,时间复杂度为O(n), 然后还需要再次进行len/2次迭代,时间复杂度为O(n/2),所以总时间复杂度为O(n) + O(n/2) = O(n).下面介绍一下什么是快慢指针.

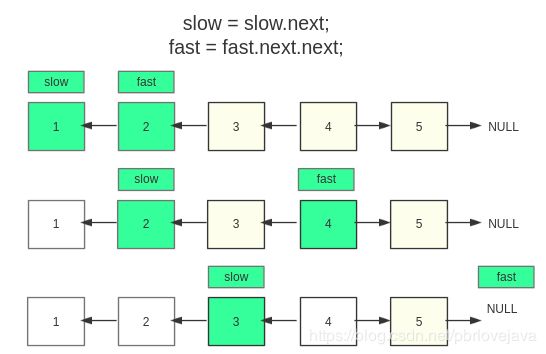
如果用快慢指针解决这个问题的话.在一开始就需要定义两个指针,一个被称为慢指针slow,一个被称为快指针fast;快指针的前进速度是慢指针的前进速度的两倍,那么当快指针到达链表尾部时,慢指针就正好在链表的中间了:

public ListNode middleNode(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

LeetCode 19. 删除链表的倒数第N个节点

给定一个链表，删除链表的倒数第 n 个节点，并且返回链表的头结点。
示例：
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后，链表变为 1->2->3->5.
说明：
给定的 n 保证是有效的。
进阶：
你能尝试使用一趟扫描实现吗？
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

使用快慢指针的思路是这样子的:
1.定义cur指向head,并且定义nFast是cur的后n个节点
2.当nFast不为null时,cur和nFast都向后走一步
3.当nFast为null时,cur即为倒数第n个节点
4.将cur的前一个节点和cur的下一个节点相连,且让cur.next=null即完成了对cur的删除
 

代码实现:

public ListNode removeNthFromEnd(ListNode head, int n) {
        if (head == null) return null;
        ListNode pre = null;
        ListNode cur = head;
        ListNode nFast = cur;
        for (int i = 0; i < n && nFast != null; i++) {
            nFast = nFast.next;
        }
        //找到需要删除的节点
        while (nFast != null) {
            pre = cur;
            cur = cur.next;
            nFast = nFast.next;
        }
        //删除节点
        if (pre != null) {
            pre.next = cur.next;
            cur.next = null;
            return head;
        }
        //被删除的是链头
        return head.next;
    }

LeetCode 141. 环形链表

给定一个链表，判断链表中是否有环。
为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。
示例 1：
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：
输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
进阶：
你能用 O(1)（即，常量）内存解决此问题吗？
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解决思路有很多种,第一种比较好想到的是采用哈希表存储每一个经过的节点地址,当有重复的节点地址时,则说明存在环,但是题目要求使用O(1)的空间复杂度解决问题,那么说明不能使用哈希表存储每个节点;所以可以考虑使用快慢指针法去解决这个问题:

我们可以列举一个生活中的场景,在一个直线型跑道上,博尔特和我一起跑100m,虽然我一定会输给他,但是我一定也可以到达终点(虽然慢了很多);但是如果我们两个人在一个400m的圆形跑道上跑由于博尔特太快了,他一定会在某一圈和我重合在一起,这就是本题能够运用快慢指针的原因:我是那个慢指针,而博尔特是那个快指针:

代码实现:

 public boolean hasCycle(ListNode head) {
        ListNode slow = head;
        ListNode fast = head;
        while (true) {
            slow = (slow == null) ? null : slow.next;
            fast = (fast == null || fast.next == null) ? null : fast.next.next;
            //都到达了终点
            if (slow == null && fast == null) return false;
            //快指针追上慢指针
            if (slow == fast) return true;
        }
    }

不定期更新, 未完持续…