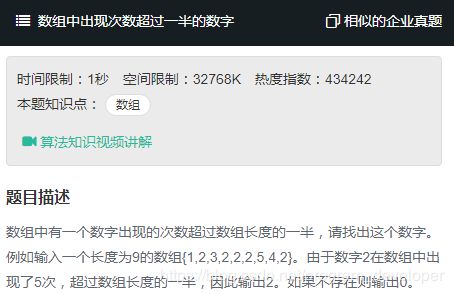
牛客网在线编程专题《剑指offer-面试题29》数组中出现次数超过一半的数字

我的个人微信公众号：Microstrong

微信公众号ID：MicrostrongAI

微信公众号介绍：Microstrong(小强)同学主要研究机器学习、深度学习、计算机视觉、智能对话系统相关内容，分享在学习过程中的读书笔记！期待您的关注，欢迎一起学习交流进步！

知乎主页：https://www.zhihu.com/people/MicrostrongAI/activities

Github：https://github.com/Microstrong0305

个人博客：https://blog.csdn.net/program_developer

 题目链接：

https://www.nowcoder.com/practice/e8a1b01a2df14cb2b228b30ee6a92163?tpId=13&tqId=11181&tPage=2&rp=2&ru=/ta/coding-interviews&qru=/ta/coding-interviews/question-ranking

题目描述：

 解题思路：

（1）方法一：快排+查找（O(nlogn)）

        看到这道题，我首先想到的是对这个数组进行排序。如果是排好序的数组，那么就能很容易统计出每个数字出现的次数。题目给出的数组没有说是排序的，因此需要先给它排序，排序的时间复杂度是 O(nlogn），然后在排完序的数组中统计出现次数超过一半的数字。

已经AC的代码：

# -*- coding:utf-8 -*-
class Solution:
    def MoreThanHalfNum_Solution(self, numbers):
        # write code here
        sortedList = self.QuickSort(numbers, 0, len(numbers) - 1)
        for i in sortedList:
            if sortedList.count(i) > len(sortedList) / 2:
                return i

        return 0

    def QuickSort(self, numList, low, high):
        if low >= high:
            return numList
        index = self.partition(numList, low, high)
        self.QuickSort(numList, low, index - 1)
        self.QuickSort(numList, index + 1, high)

        return numList

    def partition(self, numList, low, high):
        key = numList[low]
        while low < high:
            while low < high and numList[high] >= key:
                high -= 1
            numList[low] = numList[high]

            while low < high and numList[low] <= key:
                low += 1
            numList[high] = numList[low]

        numList[high] = key
        return high

if __name__ == "__main__":
    sol = Solution()
    # list = [1, 2, 3, 2, 2, 2, 5, 4, 2]
    list = [1]
    print(sol.MoreThanHalfNum_Solution(list))

（2）方法二：基于Partition函数的时间复杂度为O(n)算法

        如果我们回到题目本身仔细分析，就会发现前面的思路并没有考虑到数组的特性：数组中有一个数字出现的次数超过了数组长度的一半。如果把这个数组排序，那么排序之后位于数组中间的数字一定就是那个出现次数超过数组长度一半的数字。也就是说，这个数字就是统计学上的中位数，即长度为n的数组中第 n/2 大的数字。我们有成熟的时间复杂度为O（n）的算法得到数组中任意第k大的数字。

        这种算法受快速排序算法的启发。在随机快速排序算法中，我们先在数组中随机选择一个数字，然后调整数组中数字的顺序，使得比选中的数字小的数字都排在它的左边，比选中的数字大的数字都排在它的右边。如果这个选中的数字的下标刚好是 n/2，那么这个数字就是数组的中位数；如果它的下标大于n/2，那么中位数应该位于它的左边，我们可以接着在它的左边部分的数组中查找；如果它的下标小于n/2，那么中位数应该位于它的右边，我们可以接着在它的右边部分的数组中查找。这是一个典型的递归过程。

已经AC的代码：

# -*- coding:utf-8 -*-
class Solution:
    def MoreThanHalfNum_Solution(self, numbers):
        # write code here
        # 空列表
        if numbers == None or len(numbers) == 0:
            return 0

        middle = len(numbers) >> 1
        index = self.partition(numbers, 0, len(numbers) - 1)
        while index != middle:
            if index > middle:
                index = self.partition(numbers, 0, index - 1)
            else:
                index = self.partition(numbers, index + 1, len(numbers) - 1)

        result = numbers[middle]

        if self.CheckMoreThanHalf(numbers, result):
            return result
        else:
            return 0

    def partition(self, numList, low, high):
        key = numList[low]
        while low < high:
            while low < high and numList[high] >= key:
                high -= 1
            numList[low] = numList[high]

            while low < high and numList[low] <= key:
                low += 1
            numList[high] = numList[low]

        numList[high] = key
        return high

    def CheckMoreThanHalf(self, numbers, result):
        count = 0
        for i in numbers:
            if i == result:
                count += 1
        if count * 2 <= len(numbers):
            return False
        else:
            return True

        上述代码中的函数Partition是完成快速排序的基础，这里不再重复。在面试的时候，除了要完成基本功能即找到符合要求的数字， 还要考虑 一些无效的输入，比如输入空的数组等。此外，题目中说数组中有一个数字出现的次数超过数组长度的一半，如果输入的数组中出现频率最高的数字都没有达到这个标准，那该怎么办？这就是我们定义了一个CheckMoreThanHalf函数的原因。面试的时候我们要全面考虑这些情况，才能让面试官完全满意。

（3）解法三：根据数组特点找出O(n)的算法

       接下来我们从另外一个角度来解决这个问题。数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其他所有数字出现次数的和还要多。因此，我们可以考虑在遍历数组的时候保存两个值：一个是数组中的一个数字；另一个是次数。当我们遍历到下一个数字的时候，如果下一个数字和我们之前保存的数字相同，则次数加1；如果下一个数字和我们之前保存的数字不同，则次数减1。如果次数为零，那么我们需要保存下一个数字，并把次数设为1。由于我们要找的数字出现的次数比其他所有数字出现的次数之和还要多，那么要找的数字肯定是最后一次把次数设为1时对应的数字。

已经AC的代码：

class Solution:

    def MoreThanHalfNum_Solution(self, numbers):
        # 空列表
        if numbers == None or len(numbers) == 0:
            return 0

        result = numbers[0]
        count = 1
        for i in range(1, len(numbers) - 1):
            if count == 0:
                result = numbers[i]
                count = 1
            elif numbers[i] == result:
                count += 1
            else:
                count -= 1

        if self.CheckMoreThanHalf(numbers, result):
            return result
        else:
            return 0

    def CheckMoreThanHalf(self, numbers, result):
        count = 0
        for i in numbers:
            if i == result:
                count += 1
        if count * 2 <= len(numbers):
            return False
        else:
            return True

if __name__ == "__main__":
    sol = Solution()
    list = [1, 2, 3, 2, 2, 2, 5, 4, 2]
    list = [1]
    print(sol.MoreThanHalfNum_Solution(list))

解法比较

       上述三种算法中，第1个算法的时间复杂度为O(nlogn)，第2、3算法的时间复杂度都是O(n)。基于Partition函数的算法的时间复杂度的分析不是很直观，本文限于篇幅不作详细讨论，感兴趣的读者可以参考《算法导论》等书籍的相关章节。我们注意到，在第2种解法中，需要交换数组中数字的顺序，这就会修改输入的数组。是不是可以修改输入的数组呢？在面试的时候，我们可以和面试官讨论，让他明确需求。如果面试官说不能修改输入的数组，那就只能采用第3种解法了。

相似的题目

【1】牛客网在线编程专题《剑指offer》（29）最小的K个数，地址：https://blog.csdn.net/program_developer/article/details/82460756

【2】【算法】在N个乱序数字中查找第K大的数字，地址：https://blog.csdn.net/program_developer/article/details/82346599

【3】算法-在有序数组、无序数组中进行折半查找和二分法找无序数组中第k小（大）的数，地址：https://blog.csdn.net/program_developer/article/details/80348077

【4】字节跳动（今日头条）推荐算法实习生面试，地址：https://blog.csdn.net/program_developer/article/details/80340829

Reference

【1】《剑指offer》，何海涛著。