LASSO和L1正则包liblinear,glmnet使用和对比
LASSO算法有很多包,今天我就两个常用包liblinear和glmnet做一下分析,并给出我做分类的例子。
liblinear
LIBLINEAR是一个简单的求解大规模规则化线性分类和回归的软件包。 Liblinear是国立台湾大学的Chih-Jen Lin博士开发的,主要应对large-scale的data classification。liblinear包提供的算法包括:

我们要使用的lasso就是L1正则的logistic regression。
首先,liblinear的官方网站是:
https://www.csie.ntu.edu.tw/~cjlin/liblinear/
里面使用的lasso算法newGLMNET解法涉及到的论文是:
http://www.csie.ntu.edu.tw/~cjlin/papers/l1_glmnet/long-glmnet.pdf.
求解问题
liblinear中的lasso要求解的问题是:
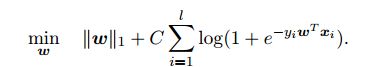
使用的newGLMNET是改进后的坐标下降,
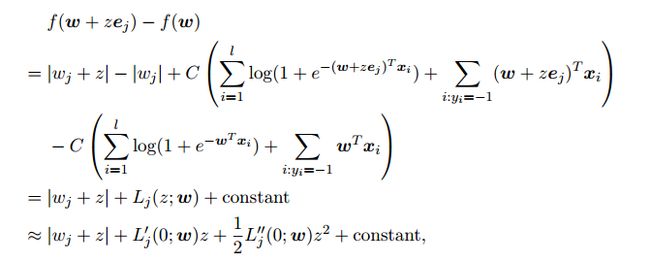
这里做了泰勒展开,因为求解二阶导涉及到hessian矩阵,而H未必满足正定条件,因此,newGLMNET增加了一个微小项:
![]()
并将原来glmnet算法中的log计算进行了近似和简化。
算法使用
主要参数如下:
-c cost : 设置参数 C(默认是1)
-p epsilon : 设置epsilon-SVR的损失函数的参数epsilon(默认是0.1)
-e epsilon : 设置迭代终止条件的容忍度tolerance
-B bias : 如果bias >= 0,那样样本x变为[x; bias],如果小于0,则不增加bias项(默认是-1)
-wi weight: 调整不同类别的参数C的权值(具体见README)
-v n: n-fold交叉检验模式。它随机的将数据划分为n个部分,然后计算它们的交叉检验准确率。
-q : 安静模式(无输出信息)liblinear实现了matlab、Java、R、Python等多种接口,具体代码不再详述。
glmnet
glmnet是一个高效实现的lasso算法求解包
glmnet官方下载地址是:
https://cran.r-project.org/web/packages/glmnet/index.html
所使用的算法细节可以在这篇论文中找到:
http://www.stanford.edu/~hastie/Papers/glmnet.pdf
github上有大神为其写了Python接口,不习惯使用R语言的可以尝试一下。
求解问题
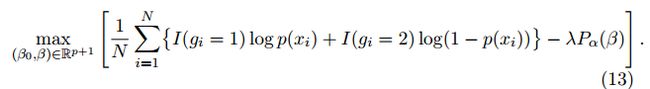
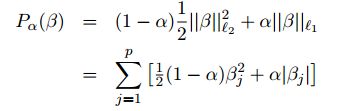
这里的P可以通过控制α参数实现Elastic Net和L2正则的求解
由上述表达式可以看出,相比liblinear,二者的lambda权重一个加在损失函数上,一个加在正则项上,使用前一定要弄清楚这一点。
LASSO回归复杂度调整的程度由参数λ来控制,λ越大对变量较多的线性模型的惩罚力度就越大,从而最终获得一个变量较少的模型。 LASSO回归与Ridge回归同属于一个被称为Elastic Net的广义线性模型家族。 这一家族的模型除了相同作用的参数λ之外,还有另一个参数α来控制应对高相关性(highly correlated)数据时模型的性状。 LASSO回归α=1,Ridge回归α=0,一般Elastic Net模型0<α<1。
算法使用
glmnet主要变量和参数如下:

参数family规定了回归模型的类型:
family="gaussian"适用于一维连续因变量(univariate)
family="mgaussian"适用于多维连续因变量(multivariate)
family="poisson"适用于非负次数因变量(count)
family="binomial"适用于二元离散因变量(binary)
family="multinomial"适用于多元离散因变量(category)这里的type.measure是用来指定交叉验证选取模型时希望最小化的目标参量,对于Logistic回归有以下几种选择:
type.measure=deviance 使用deviance,即-2倍的Log-likelihood
type.measure=mse 使用拟合因变量与实际应变量的mean squred error
type.measure=mae 使用mean absolute error
type.measure=class 使用模型分类的错误率(missclassification error)
type.measure=auc 使用area under the ROC curve,是现在最流行的综合考量模型性能的一种参数预测时的type有以下几种选择:
type=link 给出线性预测值,即进行Logit变换之前的值
type=response 给出概率预测值,即进行Logit变换之后的值
type=class 给出0/1预测值
type=coefficients 罗列出给定λ值时的模型系数
type=coefficients 罗列出给定λ值时,不为零模型系数的下标参数nlambda=50让算法自动挑选50个不同的λ值,拟合出50个系数不同的模型。 alpha=1输入α值,1是它的默认值。 值得注意的是,glmnet只能接受数值矩阵作为模型输入,如果自变量中有离散变量的话,需要把这一列离散变量转化为几列只含有0和1的向量,这个过程叫做One Hot Encoding。
最后附上我使用glmne进行二分类的完整代码,包括数据读入,数据预处理,模型构建,评价和预测:
library(Matrix)
library(glmnet)
library(SDMTools)
data <- read.csv('test.csv',header = FALSE)
index_nominal <- c(2,137,138,139,140,176,177,206)
index_numeric <- setdiff(c(1:206),index_nominal)
#上述两个是对数据中离散值和连续值列下标进行标记
#数据归一化
for (i in index_numeric){
data[,i] <- scale(data[,i],center = TRUE,scale = TRUE)
}
#数据one hot encode
for (i in index_nominal){
data[,i] <- factor(data[,i])
}
#数据采样
set.seed(2)
split <- sample(nrow(data), floor(0.5*nrow(data)))
train <-data[split,]
test <- data[-split,]
#构建测试集和训练集
train_x = train[,1:(ncol(train)-1)]
train_y = train[,ncol(train)]
matrix_train <- data.matrix(train_x)
matrix_train_y <- data.matrix(train_y)
#处理缺失值空值
matrix_train[is.na(matrix_train )] <-0
matrix_train [is.null(matrix_train )] <-0
matrix_train_y[is.na(matrix_train_y )] <-0
matrix_train_y [is.null(matrix_train_y )] <-0
#rapply( matrix_train , f=function(x) ifelse(is.nan(x),0,x), how="replace" )
#rapply( matrix_train , f=function(x) ifelse(is.infinite(x),0,x), how="replace" )
table(matrix_train_y)
#转换成matrix
test_x = test[,1:(ncol(test)-1)]
test_y = test[,ncol(test)]
matrix_test <- data.matrix(test_x)
matrix_test_y <- data.matrix(test_y)
matrix_test[is.na(matrix_test )] <-0
matrix_test [is.null(matrix_test )] <-0
matrix_test_y[is.na(matrix_test_y )] <-0
matrix_test_y [is.null(matrix_test_y )] <-0
table(matrix_test_y)
#训练模型
fit <- glmnet(matrix_train,matrix_train_y,family="binomial")
print(fit)
#交叉验证选最好的参数
cv <- cv.glmnet(matrix_train,matrix_train_y,type.measure='auc', family = "binomial")
best_lambda <- cv.glmmod$lambda.min
print(best_lambda)
#进行预测
pred<- predict(fit,newx=matrix_test,s=best_lambda,type = 'response')
confusion.matrix(matrix_test_y,pred,threshold=0.5)