对抗训练
Adversarial Training for Supervised and Semi-Supervised Learning(对抗训练在监督和半监督学习上的应用)
在对图像算法研究的过程中发现,一些机器学习方法(包括深度学习)对对抗样本非常敏感,这些对抗样本和非对抗样本非常相似,但是模型(已经在非对抗样本中训练好的模型)却会错分这些样本。为了能更好的分类该类样本,提出了对抗训练的概念,非GAN。
目录:
- 什么是对抗样本
- 产生的原因
- 产生的方法
- 抵制对抗样本
- 在文本上的应用
- 在半监督学习上的应用
什么是对抗样本
对抗样本是使得机器学习的算法产生误判的样本,如上图所示,原有的模型以57.7%的置信度判定图片为熊猫,但添加微小的扰动后,模型以99.3%的置信度认为扰动后的图片是长臂猿。
产生的原因
1、线性模型中对抗样本的产生
对于样本(x,y),希望在对x的每个维度添加微小扰动的情况下,模型得到的预测值仍然为y,即
x ^ = x + η \hat x=x+\eta x^=x+η
其中 ∥ η ∥ ∞ < ε \begin{Vmatrix}\eta\end{Vmatrix}_\infty < \varepsilon ∥∥η∥∥∞<ε
扰动的每一维都小于 ε \varepsilon ε。
对于线性模型而言,原有的权重为w,则
w T x ^ = w T x + w T η w^T\hat x = w^Tx+w^T\eta wTx^=wTx+wTη
对抗扰动使得激发增长了 ω T η ω^T\eta ωTη. 显然,我们可以让 η = s i g n ( ω ) \eta=sign(ω) η=sign(ω)来使激发增长最大。如果ω有n个维度,每个维度上平均权重为m,那么output可以增加ϵmn。
虽然 ∥ η ∥ ∞ \begin{Vmatrix}\eta\end{Vmatrix}_\infty ∥∥η∥∥∞没有随着w的维度增大而增大,但是其总的output却会随着维度n的增大而线性增长。对于高维空间而言,可以对输入进行许多无穷小的更改,这些更改加起来就是对输出的一个较大的更改。
这个例子说明,如果维度足够的话,一个简单的线性模型同样存在对抗样本的问题。过去对对抗样本的那些牵扯到神经网络的性质的解释,比如误认他们具有高度的非线性性,可能都不对。 因此,基于线性模型,对抗样本很容易生成。
2、非线性模型中对抗样本的产生
Ian假设神经网络同样是因为太“线性”而不能抵抗对抗样本。LSTMs, ReLUs, 和maxout网络都设计得很“线性”,所以他们很容易被利用。我们可以想象一个具有高度线性的网络训练出来的函数,它的高阶导数近似于0,Taylor展开以后占主导作用的是线性部分,所以可以类比为线性分类器。深度模型对对抗样本的无力最主要的还是由于其线性部分的存在。
对于非线性激活函数,在一段区间内接近为线性。神经网络在高维空间上是分段线性的(指的是输入和输出之间是线性的)。
J ( θ ; x ; y ) J(\theta; x; y) J(θ;x;y)是模型的损失函数,其中,负梯度方向 − ∇ J x ( θ ; x ; y ) -\nabla J_x(\theta; x; y) −∇Jx(θ;x;y)是模型的损失下降最快的方向,为了使 x ^ \hat x x^对模型的output产生最大的改变,正梯度方向为扰动最大的方向,在该方向上进行扰动,可以快速产生对抗样本,该方法称为“fast gradient sign method”。1
实验证明:在MNIST数据集上,使用softmax classifier 训练的模型,在对抗样本上错误率达99.9%,对抗样本上的平均置信度为79.3%;使用maxout network训练的模型,错误率为89.4% ,平均置信度为 97.6%。在CIFAR-10数据集上,maxout network 错误率为87.15% ,平均置信度为96.6%。
以下结果展示了,对抗样本产生和扰动的大小之间呈现线性相关的关系,且对抗样本可以在广泛的区域上产生。
产生的方法
1.Fast Gradient Sign Method(FGSM)
x ^ = x + ϵ s i g n ( ∇ J x ( θ ; x ; y ) ) \hat x=x+ ϵsign(\nabla J_x(\theta; x; y)) x^=x+ϵsign(∇Jx(θ;x;y))
其中梯度的方向为目标函数下降最慢的方向,得到扰动
2.Iterative FGSM(I-FGSM)
FGSM的算法在构造对抗样本的时候都只进行了一部构造,也就是沿着特定的方向在一定阈值的限制下,移动一步。而I-FGSM则通过多步更小的移动,使得能够构造出更加精准的对抗样本,但同时也提升了构造的计算量,减慢了构造的速度。
但Kurakin2 发现multi-step attack的移植性较差,即在其他模型上对抗样本不具有攻击性,因此single-step更适合用于黑盒攻击。
y L L = a r g min y p ( y ∣ X ) y_{LL} = arg\underset{y}{\min}\ p(y|X) yLL=argymin p(y∣X)
生成指定类别的对抗样本示例代码:
https://www.anishathalye.com/2017/07/25/synthesizing-adversarial-examples/?spm=5176.100239.blogcont149583.28.NUZKV8
4.RANDOM-FGSM
该算法在论文Ensemble Adversarial Training Attacks and Defenses中提出,提出的原因主要是认为:在数据点附近的损失函数会有很大的曲率,也就是不够平滑,从而导致生成的对抗样本会对自身的模型有特异性,这也解释了为什么经过对抗训练的模型对于白盒攻击的鲁棒性比黑盒攻击的鲁棒性更好这个奇怪的现象。
抵制对抗样本
显然我们希望模型可以变得更加鲁棒。一个最简单的方法,就是生成这些数据,并且把这些数据加入到训练数据中。这样模型就会正视这些数据,并且尽可能地拟合这些数据,最终完成了模型拟合,这些盲区也就覆盖住了。将对抗样本和原有数据一起进行训练,对抗样本产生的损失作为原损失的一部分,即在不修改原模型结构的情况下增加模型的loss,产生正则化的效果。
![]()
其中 θ ^ \hat \theta θ^代表在产生对抗样本的过程中,梯度不变
![]()
代码示例:
https://github.com/tensorflow/cleverhans
对于keras代码,可以先转化为tf model,使用tf 的形式进行训练,keras转化为tf进行训练的参考网址:
https://blog.keras.io/keras-as-a-simplified-interface-to-tensorflow-tutorial.html
https://towardsdatascience.com/freezing-a-keras-model-c2e26cb84a38
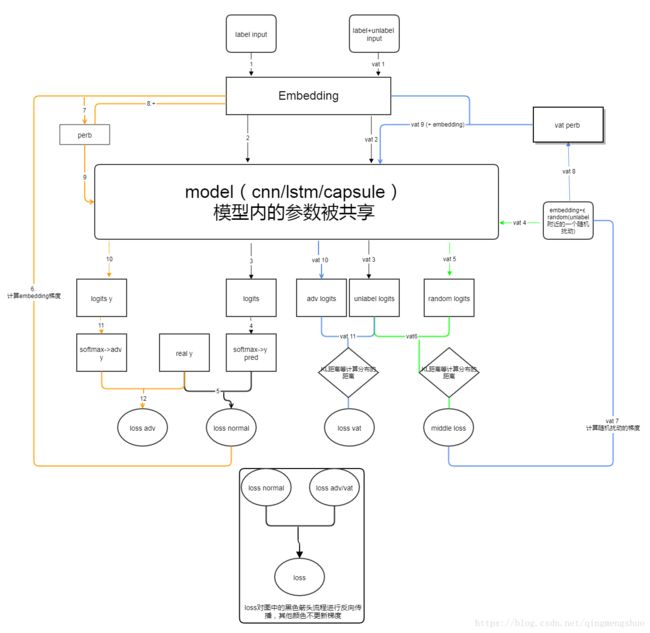
在文本上的应用
由于文本不同于图片,文本一般转化为Index,通过Embedding后输入到network中,无法对input进行直接的求导,Miyato3 等提出将扰动添加到Embedding层,经过扰动后的Embedding对扰动有更好的鲁棒性。其模型结构为
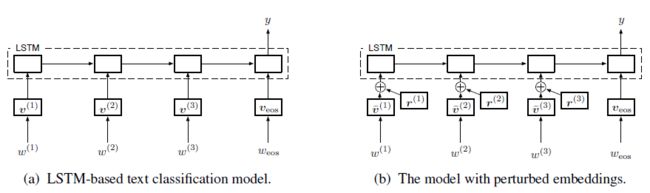
采用预训练的LSTM模型作为分类的结构,在实际应用中,可以替换成其他的网络。
由于Embedding层可以学习比较大范围的变化,使得扰动变的无关紧要,因此可以将embedding层进行归一化,使数值限定在指定的大小区间内。

在半监督学习上的应用
由于存在大量无标签的数据,标签数据的获取代价会比较大,Miyato3提出了在unlabel数据上运用对抗训练的方法。
其中 L a d v ( x l , θ ) L_{adv}(x_l,\theta) Ladv(xl,θ)是衡量真实分布 q ( y ∣ x l ) q(y|x_l) q(y∣xl)和预测分布 p ( y ∣ x l + r a d v , θ ) p(y|x_l+r_{adv},\theta) p(y∣xl+radv,θ)差距的非负函数, x ∗ x_* x∗包含 x l a b e l x_{label} xlabel和 x u n l a b e l x_{unlabel} xunlabel(以下简写为 x l x_l xl, x u l x_{ul} xul)。而 r a d v r_{adv} radv使2者之间的距离最大。
由于 q ( y ∣ x ) q(y|x) q(y∣x)是真实分布,无法预先得到,但是在标记样本足够多的情况下,已经预训练好的模型分布 p ( y ∣ x ) p(y|x) p(y∣x)接近于真实分布 q ( y ∣ x ∗ ) q(y|x_*) q(y∣x∗),因此可以使用 p ( y ∣ x ) p(y|x) p(y∣x)替代 q ( y ∣ x ) q(y|x) q(y∣x)。
对于无标签数据,可以采用上一阶段的对unlabel数据的预测结果(logits)作为无标签数据的(虚拟)标签,在虚拟标签上计算对抗方向。因此对抗样本的目标为:
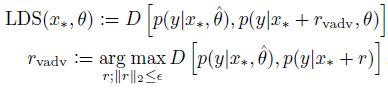
对抗样本产生的误差为:
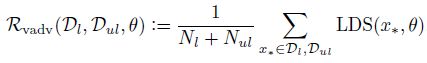
总的损失为:
![]()
其中 L ( D l , θ ) L(D_l,\theta) L(Dl,θ)是 x l x_l xl上的negative log-likelihood。
r a d v r_{adv} radv的求解
求解 r a d v 的 先 验 知 识 : r_{adv}的先验知识: radv的先验知识:power iterator 方法
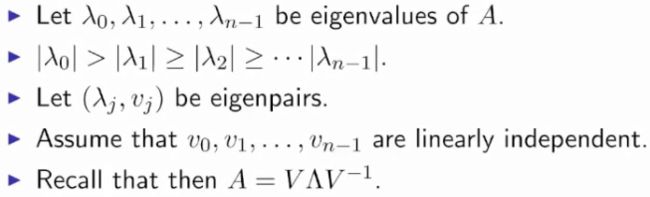
x ( 0 ) x^{(0)} x(0)为随机初始化的向量:

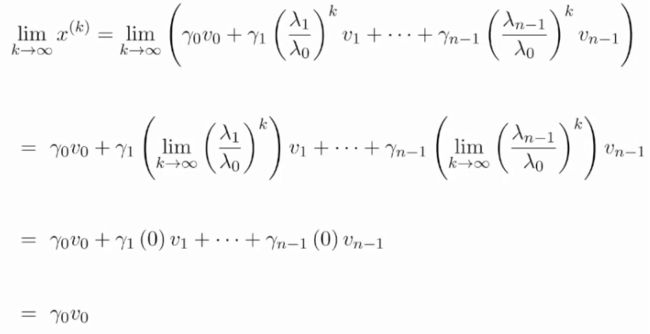
假设所有的 v 0 v_0 v0都是单位向量,可以推断以下結果:
x ( k + 1 ) = γ 0 v 0 ∥ γ 0 v 0 ∥ = v 0 x^{(k+1)}=\frac {\gamma_0 v_0 }{ \begin{Vmatrix}\gamma_0 v_0\end{Vmatrix}} = v_0 x(k+1)=∥∥γ0v0∥∥γ0v0=v0
x ( k + 1 ) x^{(k+1)} x(k+1)收敛于最大的特征向量。
参考视频:https://www.youtube.com/watch?v=OzeDqsVoTFc
参考文档:https://en.wikipedia.org/wiki/Power_iteration
因此特征向量可以通过迭代的方式计算得到:
A x 0 → A x 1 → x k + 1 ≈ v 0 Ax_0 \rightarrow Ax_1 \rightarrow x_{k+1} \approx v_0 Ax0→Ax1→xk+1≈v0
r a d v r_{adv} radv的求解
由于 D ( r ; x ∗ ; θ ) = D [ p ( y ∣ x ∗ , θ ^ ) , p ( y ∣ x ∗ + r , θ ) ] D(r; x_*; \theta)=D[p(y|x_*,\hat \theta ),p(y|x_*+r,\theta )] D(r;x∗;θ)=D[p(y∣x∗,θ^),p(y∣x∗+r,θ)] 是连续函数,在 r = 0 r=0 r=0时,D取得最小值,因此无法求得 r a d v = ϵ s i g n ( ∇ J x ( θ ; x ; y ) ) r_{adv} =ϵsign(\nabla J_x(\theta; x; y)) radv=ϵsign(∇Jx(θ;x;y))。以下介绍一种快速求 r a d v r_{adv} radv的方法:
假设 D ( r ; x ∗ ; θ ) D(r; x_*; \theta) D(r;x∗;θ)在x与 θ ^ \hat \theta θ^处处二阶可微,由于 r = 0 时 , D r = 0 = 0 , ∇ D r = 0 = 0 ; r=0时,D_{r=0}=0 ,\nabla D_{r=0} = 0; r=0时,Dr=0=0,∇Dr=0=0;因此根据泰勒展开式:
D ( r ; x ; θ ^ ) ≈ 1 2 r T H ( x ; θ ^ ) r D(r; x; \hat \theta)\approx\frac 12 r^T H(x;\hat \theta) r D(r;x;θ^)≈21rTH(x;θ^)r
其中 H ( x ; θ ^ ) H(x;\hat \theta) H(x;θ^)为D的hession矩阵
H ( x ; θ ^ ) = ∇ ∇ r D ( r ; x ; θ ^ ) ∣ r = 0 . H(x;\hat \theta)=\nabla \nabla _r D(r; x;\hat \theta )|{r=0}. H(x;θ^)=∇∇rD(r;x;θ^)∣r=0.
而 r a d v r_{adv} radv使 H ( x ; θ ^ ) H(x;\hat \theta) H(x;θ^)取得最大值:
r a d v ≈ a r g min r r T H ( x ; θ ^ ) r ; ∥ r ∥ 2 ≤ ε r_{adv} \approx arg \underset{r}{\min}\ r^T H(x;\hat \theta) r ;\begin{Vmatrix}r\end{Vmatrix}_2 \le \varepsilon radv≈argrmin rTH(x;θ^)r;∥∥r∥∥2≤ε
由于 H ( x ; θ ^ ) H(x;\hat \theta) H(x;θ^)为对称矩阵,对于对称矩阵均可合同于一个对角矩阵,
r T H ( x ; θ ^ ) r = Λ ; r 为 特 征 向 量 r^T H(x;\hat \theta) r = \Lambda;r为特征向量 rTH(x;θ^)r=Λ;r为特征向量
因此可转化为求 H ( x ; θ ^ ) H(x;\hat \theta) H(x;θ^)的特征值和特征向量的问题。power iterator方法可以在H比较难求解的情况下,通过迭代的方式计算特征值和特征向量。
根据power iterator方法可得
r a d v ≈ ε μ ˉ ; μ ˉ 为 单 位 向 量 r_{adv} \approx {\varepsilon \bar\mu};\bar\mu为单位向量 radv≈εμˉ;μˉ为单位向量
μ ˉ ← H x 0 ˉ ( d ← H d ˉ ) , 其 中 x 0 / d 是 随 机 初 始 化 的 一 个 向 量 \bar\mu \leftarrow \bar{Hx_0} (d \leftarrow \bar{Hd} ),其中x_0/d是随机初始化的一个向量 μˉ←Hx0ˉ(d←Hdˉ),其中x0/d是随机初始化的一个向量
H d ˉ \bar{Hd} Hdˉ的求解可以根据差分法可得:
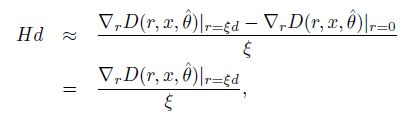
![]()
其中
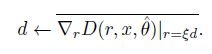
因此最大的扰动方向为,x附近随机扰动点的梯度方向

根据实验可得,在获取 d ← H d ˉ d \leftarrow \bar{Hd} d←Hdˉ的过程中,迭代一次即可获得比较好的效果。
示例代码地址:
https://github.com/tensorflow/models/tree/master/research/adversarial_text
总结
[1]: Ian Goodfellow, Jonathon Shlens, and Christian Szegedy. Explaining and harnessing adversarial examples. In ICLR, 2015.
[2]: Takeru Miyato, Andrew M Dai, Ian Goodfellow. Adversarial training methods for semi-supervised text classification. 2017.
[3]: Takeru Miyato, Shin-ichi Maeda, Masanori Koyama, Ken Nakae, and Shin Ishii. Distributional smoothing with
virtual adversarial training. In ICLR, 2016.
[4]: Alexey Kurakin,Ian J. Goodfellow,Samy Bengio.Adversarial machine learning at scale. ICLR 2017.
[5]:Takeru Miyato, Shin-ichi Maeda, Masanori Koyama, Shin Ishii. Virtual Adversarial Training:A Regularization Method for Supervised and Semi-Supervised Learning. IEEE Transactions on Pattern Analysis and Machine Intelligence,2018.
注脚的解释 ↩︎
注脚的解释
3.Targeted FGSM
与FGSM主要的区别是,FGSM将样本沿着梯度下降的反方向构造样本,而targeted FGSM沿着希望模型误判的class的方向构造 ↩︎注脚的解释 ↩︎ ↩︎