C语言实现二叉堆及应用

前段时间学到二叉堆的应用，现在来总结一下。

目录

二叉堆的概念

二叉堆的存储

二叉堆基本操作

节点插入(上浮调整)

节点删除(下沉调整)

构建二叉堆

二叉堆基本应用

二叉堆应用于堆排序

二叉堆应用于优先队列

---

---

二叉堆的概念

   二叉堆本质是一种完全二叉树，所以完全二叉树的特点和性质可以运用到二叉堆。二叉堆可分为最小堆和最大堆。

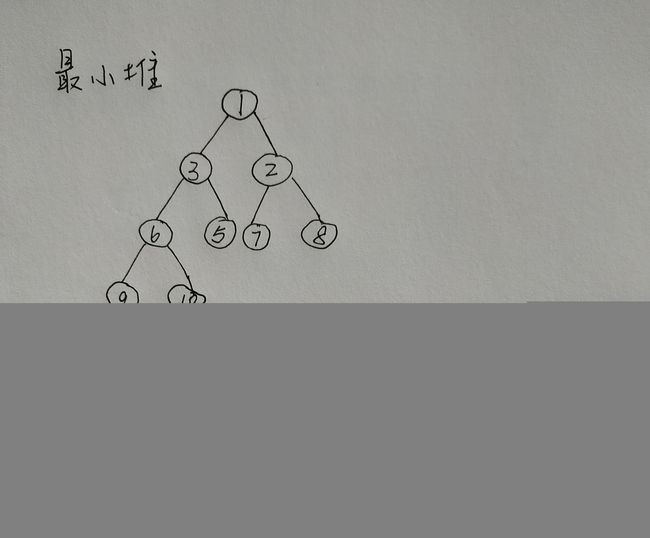
  最小堆定义：最小堆的任何一个父节点的值，都小于等于它左右孩子节点的值。

  最大堆定义：最大堆的任何一个父节点的值，都大于等于它左右孩子节点的值。

  二叉堆用到了递归定义，根据这个特点，我们可以知道最小堆的根节点是所有节点中值最小的，最大堆的根节点是所有节点中值最大的。

二叉堆的存储

   二叉堆的存储方式是顺序存储，即用数组存储。如下图所示：

根据完全二叉树的特点，当存储从下标0开始时，父节点的下标parentIndex和它左右孩子节点的下标满足以下关系：

左孩子节点下标 = 2 * parentIndex + 1；

右孩子节点下标 =  2 * parentIndex + 2；

当孩子节点的下标为childIndex时(左右孩子都适用)，其父节点的下标 = (childIndex - 1) / 2; (注意这边是取整)

 

二叉堆基本操作

节点插入(上浮调整)

   二叉堆节点插入过程:在最后一个节点的下个位置插入新元素，插入新元素后需要重新调整二叉堆。以最小堆举例，如果新元素的值比它的父节点的值小，需要把新元素的值和父节点的值进行交换，接着再重复上面的步骤，知道比较到根节点为止。代码实现如下:

/**
*@desc 上浮调整
*@param arr array 待调整的堆
*@param length 堆的大小
*@ret
*/
void upAdjust(int * arr, int length){
   int childIndex = length - 1;
   int parentIndex = (childIndex - 1)/2;
   int temp = 0;
   while(childIndex > 0 && arr[childIndex] < arr[parentIndex]){//调整的条件:子节点的值小于父节点的值
    temp = arr[childIndex];
    arr[childIndex] = arr[parentIndex];
    arr[parentIndex] = temp;
    childIndex = parentIndex;
    parentIndex = (childIndex - 1)/2;
   }
}

节点删除(下沉调整)

二叉堆节点删除过程:二叉堆一般删除的是根节点，但并不是真正的删除，而是把根节点替换到二叉堆的最后一个节点，把最后一个节点替换到根节点，接着再重新调整二叉堆。以最小堆为例，调整的过程为，比较根节点的值和左右孩子节点的值，如果根节点的值小于左右孩子节点的值，无需交换，否则根节点和左右孩子中最小的一个节点进行交换，重复上面步骤，直到比较到叶子节点为止。比较的过程可用循环进行实现，代码如下：

/**
*@desc 下沉调整
*@param arr array 待调整的堆
*@param parentIndex int 要调整的节点
*@param length 堆的大小
*@ret
*/
void downAdjust(int * arr, int parentIndex, int length){
  int childIndex = 2 * parentIndex + 1;
  int tmp;
  while(childIndex < length){
    if((childIndex + 1) < length && arr[childIndex+1] < arr[childIndex]){//如果存在右孩子而且右孩子比左孩子小,则和父节点比较的索引定位到右孩子
       childIndex++;
   }
   if(arr[childIndex] > arr[parentIndex]){//父节点大于两孩子节点，无需调整，直接跳出
        break;
   }
   tmp = arr[childIndex];
   arr[childIndex] = arr[parentIndex];
   arr[parentIndex] = tmp;
   parentIndex = childIndex;
   childIndex = 2 * parentIndex + 1;
}
}

构建二叉堆

构建二叉堆的过程实质是将所有非叶子节点做下沉调整，从最后一个非叶子节点开始直到根节点。代码实现如下：

/**
*@desc 构建二叉堆
*@param arr array 待调整的完全二叉树
*@param length 堆的大小
*@ret
*/
void buildHeap(int * arr, int length){
 for(int i = (length - 2)/2; i >= 0;i--){//从最后一个非叶子结点开始，依次下沉非叶子结点
    downAdjust(arr, i, length);
 }
}

二叉堆基本应用

二叉堆应用于堆排序

由于二叉堆的特点，堆顶元素是所有节点中值最大或者最小的元素，因此我们只要循环删除堆顶节点，把堆顶元素交换到最后一个元素，直到删除只剩下一个节点，得到的数组就是个有序数组。最大堆实现的是升序排序，最小堆实现的是降序排序。以最小堆为例，下面代码实现了降序排序。

/**
*@desc 实现堆排序
*@param arr array 待排序的数组
*@param length 堆的大小
*@ret
*/
void heapSort(int * arra, int length){
//堆排序过程:
//1.将无序数组调整为二叉堆
//2.循环删除堆顶元素,替换堆的最后一个元素
 int i,tmp;
 buildHeap(arra, length);//调整为二叉堆
 for(i = length - 1; i > 0; i--){
    //交换堆顶元素和最后一个元素
    tmp = arra[0];
    arra[0] = arra[i];
    arra[i] = tmp;
    downAdjust(arra, 0, i);//重新调整二叉堆
 }
}

二叉堆应用于优先队列

   普通队列具有先进先出的特点，这因为，队列是一种受限的线性表，只允许一端插入，一端删除。

   那什么是优先队列呢？优先队列具有普通队列的特点，但一点不同的是，优先队列每次出队的是，队列中最大或者最小的元素。

  根据上面这些，我们很容易想到可以二叉堆来实现优先队列，出队对应二叉堆删除节点操作，入队对应二叉堆插入节点的操作。由于二叉堆的特点，堆顶元素是最大或者最小元素，对应出队时最大或者最小的元素。

   以上就是对二叉堆的总结。