Java版数据结构和算法学习笔记之树结构篇
Java版数据结构和算法学习笔记之树结构篇
- 1. 树结构概述
- 1.1 什么是树结构
- 1.2 为什么使用树结构
- 1.3 树的基本概念
- 2. 二叉树
- 2.1 什么是二叉树
- 2.2 链式存储的二叉树
- 2.2.1 二叉树代码实现
- 2.2.2 二叉树的遍历
- 2.2.3 二叉树的查找
- 2.2.4 删除二叉树的子树
- 2.2.5 部分代码改进
- 2.3 顺序存储的二叉树
- 2.3.1 基本概念
- 2.3.2 顺序二叉树的遍历
- 3. 线索二叉树
- 3.1 基本概念
- 3.2 线索二叉树的实现
- 3.3 二叉树的遍历
- 4. 赫夫曼树
- 4.1 什么是赫夫曼树
- 4.2 赫夫曼树的创建
- 4.3 赫夫曼编码
- 4.4 赫夫曼译码
- 5. 二叉排序树(二叉查找树)
- 5.1 概述
- 5.2 代码实现
- 6. AVL树---平衡二叉树
- 6.1 为什么要用平衡二叉树
- 6.2 平衡二叉树定义
- 6.3 平衡二叉树关键问题
- 6.3.1 如何求树的高度
- 6.3.2 关于树的旋转
- 6.3.3 小结
- 6.4 平衡二叉树实现代码
- 7. 多路查找树
- 7.1 计算机存储方式
- 7.1.1硬盘
- 7.1.2 内存
- 7.2 2-3树---B树的一种特例
- 7.3 2-3-4树
- 7.4 B树
1. 树结构概述
1.1 什么是树结构
1.2 为什么使用树结构
查找和插入操作均比线性结构好。
1.3 树的基本概念
-
根节点是数据结构中,用来描述“树”型结构的名词。
这种结构像一根倒着的树,每片树叶都长在一个结点上,这个结点就叫做这个叶子的父结点,这个叶子叫做你结点的子结点,没有子结点的结点叫叶子结点,没有父结点的结点叫根结点。
-
双亲节点实际上就是父节点。
-
节点的度: 一个结点的子结点数。
-
节点的权:节点中存的数字。
-
子树
-
层
-
树的高度:最大的层数。
-
森林:森林(forest)是m(m≥0)棵互不相交的树的集合。任何一棵树,删除了根结点就变成了森林。
2. 二叉树
2.1 什么是二叉树
任何一个结点的子结点数量均不超过2。
二叉树的子结点分为左结点和右结点,且左结点与右结点不能随意颠倒位置。
满二叉树:
所以叶子节点都在最后一层,且结点总数为2n-1,n为树的高度/层数。
完全二叉树
所有叶子节点都在最后一层或倒数第二层,且最后一层的叶子结点在左边连续,倒数第二次的叶子结点在右边连续。
注意:满二叉树实际上就是完全二叉树。没有任何结点的树是空树。
2.2 链式存储的二叉树
2.2.1 二叉树代码实现
package Tree;
public class TreeNode {
//节点的权
int value;
//左结点
TreeNode leftNode;
//右结点
TreeNode rightNode;
public TreeNode(int value){
this.value=value;
}
//设置左结点
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右结点
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public TreeNode getLeftNode() {
return leftNode;
}
public TreeNode getRightNode() {
return rightNode;
}
}
package Tree;
public class BinaryTree {
TreeNode root;
//设置根结点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根结点
public TreeNode getRoot() {
return root;
}
}
package Tree;
public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree=new BinaryTree();
//创建一个根结点
TreeNode root=new TreeNode(1);
//把根节点赋给tree
binaryTree.setRoot(root);
//创建root的左结点
TreeNode rootL=new TreeNode(2);
root.setLeftNode(rootL);
//创建root的右结点
TreeNode rootR=new TreeNode(3);
root.setRightNode(rootR);
//输出根结点的值
System.out.println(binaryTree.getRoot().getValue());
//输出左结点的值
System.out.println(root.getLeftNode().getValue());
//输出左结点的值
System.out.println(root.getRightNode().getValue());
}
}
2.2.2 二叉树的遍历
-
前序遍历
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。
-
中序遍历
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
-
后序遍历
首先遍历左子树,然后遍历右子树,最后访问根结点。
-
例如:
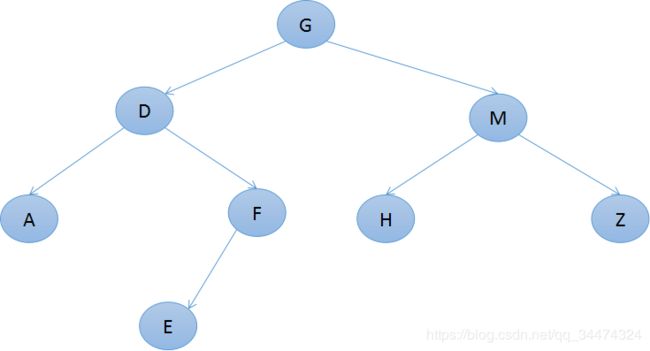
前序遍历:GDAFEMHZ
中序遍历:ADEFGHMZ
后续遍历:AEFDHZMG
- 又如:
- 代码实现:主要是利用递归的思想
package Tree;
public class BinaryTree {
TreeNode root;
//设置根结点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根结点
public TreeNode getRoot() {
return root;
}
public void frontShow(){
root.frontShow();
}
public void mediumShow(){
root.mediumShow();
}
public void afterShow(){
root.afterShow();
}
}
package Tree;
public class TreeNode {
//节点的权
int value;
//左结点
TreeNode leftNode;
//右结点
TreeNode rightNode;
public TreeNode(int value){
this.value=value;
}
//设置左结点
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右结点
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public TreeNode getLeftNode() {
return leftNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void frontShow(){
System.out.print(this.value+" ");
if(leftNode!=null) {
leftNode.frontShow();
}
if(rightNode!=null) {
rightNode.frontShow();
}
}
public void mediumShow(){
if(leftNode!=null) {
leftNode.mediumShow();
}
System.out.print(this.value+" ");
if(rightNode!=null) {
rightNode.mediumShow();
}
}
public void afterShow(){
if(leftNode!=null) {
leftNode.afterShow();
}
if(rightNode!=null) {
rightNode.afterShow();
}
System.out.print(this.value+" ");
}
}
package Tree;
public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree=new BinaryTree();
//创建一个根结点
TreeNode root=new TreeNode(1);
//把根节点赋给tree
binaryTree.setRoot(root);
//创建root的左结点
TreeNode rootL=new TreeNode(2);
root.setLeftNode(rootL);
//创建root的右结点
TreeNode rootR=new TreeNode(3);
root.setRightNode(rootR);
//为第二层的左结点创建两个子结点
rootL.setLeftNode(new TreeNode(4));
rootL.setRightNode(new TreeNode(5));
//为第二层的右结点创建两个子结点
rootR.setLeftNode(new TreeNode(6));
rootR.setRightNode(new TreeNode(7));
//树遍历
System.out.print("前序遍历: ");
binaryTree.frontShow();
System.out.print("\n"+"中序遍历: ");
binaryTree.mediumShow();
System.out.print("\n"+"后序遍历: ");
binaryTree.afterShow();
}
}
2.2.3 二叉树的查找
以前序查找为例。
package Tree;
public class BinaryTree {
TreeNode root;
//设置根结点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根结点
public TreeNode getRoot() {
return root;
}
public void frontShow(){
root.frontShow();
}
public void mediumShow(){
root.mediumShow();
}
public void afterShow(){
root.afterShow();
}
public TreeNode frontSearch(int i){
return root.frontSearch(i);
}
}
package Tree;
public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree=new BinaryTree();
//创建一个根结点
TreeNode root=new TreeNode(1);
//把根节点赋给tree
binaryTree.setRoot(root);
//创建root的左结点
TreeNode rootL=new TreeNode(2);
root.setLeftNode(rootL);
//创建root的右结点
TreeNode rootR=new TreeNode(3);
root.setRightNode(rootR);
//为第二层的左结点创建两个子结点
rootL.setLeftNode(new TreeNode(4));
rootL.setRightNode(new TreeNode(5));
//为第二层的右结点创建两个子结点
rootR.setLeftNode(new TreeNode(6));
rootR.setRightNode(new TreeNode(7));
//树遍历
System.out.print("前序遍历: ");
binaryTree.frontShow();
System.out.print("\n"+"中序遍历: ");
binaryTree.mediumShow();
System.out.print("\n"+"后序遍历: ");
binaryTree.afterShow();
//前序查找
TreeNode t=binaryTree.frontSearch(9);
System.out.println(t);
}
}
package Tree;
public class TreeNode {
//节点的权
int value;
//左结点
TreeNode leftNode;
//右结点
TreeNode rightNode;
public TreeNode(int value) {
this.value = value;
}
//设置左结点
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右结点
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public TreeNode getLeftNode() {
return leftNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void frontShow() {
System.out.print(this.value + " ");
if (leftNode != null) {
leftNode.frontShow();
}
if (rightNode != null) {
rightNode.frontShow();
}
}
public void mediumShow() {
if (leftNode != null) {
leftNode.mediumShow();
}
System.out.print(this.value + " ");
if (rightNode != null) {
rightNode.mediumShow();
}
}
public void afterShow() {
if (leftNode != null) {
leftNode.afterShow();
}
if (rightNode != null) {
rightNode.afterShow();
}
System.out.print(this.value + " ");
}
public TreeNode frontSearch(int i) {
TreeNode target=null;
if (this.value == i) {
return this;
} else {
if (target==null&leftNode != null) {
target=leftNode.frontSearch(i);
}
if (target==null&rightNode != null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
}
2.2.4 删除二叉树的子树
package Tree;
public class BinaryTree {
TreeNode root;
//设置根结点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根结点
public TreeNode getRoot() {
return root;
}
public void frontShow(){
root.frontShow();
}
public void mediumShow(){
root.mediumShow();
}
public void afterShow(){
root.afterShow();
}
public TreeNode frontSearch(int i){
return root.frontSearch(i);
}
public void delete(int i){
if(root.value==i){
root=null;
}else{
root.delete(i);
}
}
}
package Tree;
public class TestBinaryTree {
public static void main(String[] args) {
//创建一棵树
BinaryTree binaryTree=new BinaryTree();
//创建一个根结点
TreeNode root=new TreeNode(1);
//把根节点赋给tree
binaryTree.setRoot(root);
//创建root的左结点
TreeNode rootL=new TreeNode(2);
root.setLeftNode(rootL);
//创建root的右结点
TreeNode rootR=new TreeNode(3);
root.setRightNode(rootR);
//为第二层的左结点创建两个子结点
rootL.setLeftNode(new TreeNode(4));
rootL.setRightNode(new TreeNode(5));
//为第二层的右结点创建两个子结点
rootR.setLeftNode(new TreeNode(6));
rootR.setRightNode(new TreeNode(7));
//树遍历
System.out.print("前序遍历: ");
binaryTree.frontShow();
System.out.print("\n"+"中序遍历: ");
binaryTree.mediumShow();
System.out.print("\n"+"后序遍历: ");
binaryTree.afterShow();
//前序查找
TreeNode t=binaryTree.frontSearch(3);
System.out.println(t);
//删除子树
binaryTree.delete(5);
binaryTree.frontShow();
//前序查找
TreeNode t1=binaryTree.frontSearch(3);
System.out.println(t1);
}
}
package Tree;
public class TreeNode {
//节点的权
int value;
//左结点
TreeNode leftNode;
//右结点
TreeNode rightNode;
public TreeNode(int value) {
this.value = value;
}
//设置左结点
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右结点
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public TreeNode getLeftNode() {
return leftNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void frontShow() {
System.out.print(this.value + " ");
if (leftNode != null) {
leftNode.frontShow();
}
if (rightNode != null) {
rightNode.frontShow();
}
}
public void mediumShow() {
if (leftNode != null) {
leftNode.mediumShow();
}
System.out.print(this.value + " ");
if (rightNode != null) {
rightNode.mediumShow();
}
}
public void afterShow() {
if (leftNode != null) {
leftNode.afterShow();
}
if (rightNode != null) {
rightNode.afterShow();
}
System.out.print(this.value + " ");
}
public TreeNode frontSearch(int i) {
TreeNode target=null;
if (this.value == i) {
return this;
} else {
if (target==null&leftNode != null) {
target=leftNode.frontSearch(i);
}
if (target==null&rightNode != null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
public void delete(int i){
TreeNode parent=this;
if(parent.leftNode!=null&&parent.leftNode.value==i){
this.leftNode=null;
return;
}
if(parent.rightNode!=null&&parent.rightNode.value==i){
this.rightNode=null;
return;
}
parent=leftNode;
if(parent!=null){
parent.delete(i);
}
parent=rightNode;
if (parent!=null){
parent.delete(i);
}
}
}
2.2.5 部分代码改进
package Tree;
public class BinaryTree {
TreeNode root;
//设置根结点
public void setRoot(TreeNode root) {
this.root = root;
}
//获取根结点
public TreeNode getRoot() {
return root;
}
public void frontShow(){
if(root!=null){
root.frontShow();
}
}
public void mediumShow() {
if (root != null) {
root.mediumShow();
}
}
public void afterShow() {
if (root != null) {
root.afterShow();
}
}
public TreeNode frontSearch(int i){
return root.frontSearch(i);
}
public void delete(int i){
if(root.value==i){
root=null;
}else{
root.delete(i);
}
}
}
优秀博客1
优秀博客2
2.3 顺序存储的二叉树
2.3.1 基本概念
顺序存储的二叉树通常情况只考虑完全二叉树。
- 第n个结点的左子结点是2*n+1
- 第n个结点的右子结点是2*n+2
- 第n个结点的父结点是(n-1)/2
2.3.2 顺序二叉树的遍历
package ArrayTree;
public class ArrayBinaryTree {
int[] data;
public ArrayBinaryTree(int[] data){
this.data=data;
}
public void frontShow(int start){
if(this.data==null||data.length==0){
return;
}
//先遍历当前内容
System.out.print(data[start]+" ");
//再遍历左结点
if(2*start+1package ArrayTree;
public class TestAraayBinaryTree {
public static void main(String[] args) {
int[] data={1,2,3,4,5,6,7};
ArrayBinaryTree tree=new ArrayBinaryTree(data);
tree.frontShow(0);
}
}
3. 线索二叉树
3.1 基本概念
百度百科之线索二叉树
- 线索化二叉树时,一个结点的前一个结点叫前驱结点。
- 线索化二叉树时,一个结点的后一个结点叫后继结点。
3.2 线索二叉树的实现
package ThreadedTree;
public class TestThreadedBinaryTree {
public static void main(String[] args) {
//创建一棵树
ThreadedBinaryTree binaryTree=new ThreadedBinaryTree();
//创建一个根结点
ThreadedtreeNode root=new ThreadedtreeNode(1);
//把根节点赋给tree
binaryTree.setRoot(root);
//创建root的左结点
ThreadedtreeNode rootL=new ThreadedtreeNode(2);
root.setLeftNode(rootL);
//创建root的右结点
ThreadedtreeNode rootR=new ThreadedtreeNode(3);
root.setRightNode(rootR);
//为第二层的左结点创建两个子结点
rootL.setLeftNode(new ThreadedtreeNode(4));
ThreadedtreeNode fiveNode=new ThreadedtreeNode(5);
rootL.setRightNode(fiveNode);
//为第二层的右结点创建两个子结点
rootR.setLeftNode(new ThreadedtreeNode(6));
rootR.setRightNode(new ThreadedtreeNode(7));
//树遍历
System.out.print("前序遍历: ");
binaryTree.frontShow();
System.out.print("\n"+"中序遍历: ");
binaryTree.mediumShow();
System.out.print("\n"+"后序遍历: ");
binaryTree.afterShow();
//中序线索化二叉树
binaryTree.threadedNodes();
System.out.println("验证中序线索二叉树功能:");
System.out.println(fiveNode.leftNode.value);
System.out.println(fiveNode.leftNode.leftType);
}
}
package ThreadedTree;
public class ThreadedBinaryTree {
ThreadedtreeNode root;
//前驱结点
ThreadedtreeNode pre;
//设置根结点
public void setRoot(ThreadedtreeNode root) {
this.root = root;
}
public void threadedNodes(){
threadedNodes(root);
}
//中序线索化二叉树
public void threadedNodes(ThreadedtreeNode node){
if(node==null){
return;
}
//处理左子树
threadedNodes(node.leftNode);
//处理前驱结点
if(node.leftNode==null){
node.leftNode=pre;
node.leftType=1;
}
if(pre!=null&&pre.rightNode==null){
pre.rightNode=node;
pre.rightType=1;
}
pre=node;
//处理右子树
threadedNodes(node.rightNode);
}
//获取根结点
public ThreadedtreeNode getRoot() {
return root;
}
public void frontShow(){
if(root!=null){
root.frontShow();
}
}
public void mediumShow() {
if (root != null) {
root.mediumShow();
}
}
public void afterShow() {
if (root != null) {
root.afterShow();
}
}
public ThreadedtreeNode frontSearch(int i){
return root.frontSearch(i);
}
public void delete(int i){
if(root.value==i){
root=null;
}else{
root.delete(i);
}
}
}
package ThreadedTree;
public class ThreadedtreeNode {
//节点的权
int value;
//左指针
ThreadedtreeNode leftNode;
//右指针
ThreadedtreeNode rightNode;
//标识指针类型
int leftType;
int rightType;
public ThreadedtreeNode(int value) {
this.value = value;
}
//设置左结点
public void setLeftNode(ThreadedtreeNode leftNode) {
this.leftNode = leftNode;
}
//设置右结点
public void setRightNode(ThreadedtreeNode rightNode) {
this.rightNode = rightNode;
}
public int getValue() {
return value;
}
public ThreadedtreeNode getLeftNode() {
return leftNode;
}
public ThreadedtreeNode getRightNode() {
return rightNode;
}
public void frontShow() {
System.out.print(this.value + " ");
if (leftNode != null) {
leftNode.frontShow();
}
if (rightNode != null) {
rightNode.frontShow();
}
}
public void mediumShow() {
if (leftNode != null) {
leftNode.mediumShow();
}
System.out.print(this.value + " ");
if (rightNode != null) {
rightNode.mediumShow();
}
}
public void afterShow() {
if (leftNode != null) {
leftNode.afterShow();
}
if (rightNode != null) {
rightNode.afterShow();
}
System.out.print(this.value + " ");
}
public ThreadedtreeNode frontSearch(int i) {
ThreadedtreeNode target=null;
if (this.value == i) {
return this;
} else {
if (target==null&leftNode != null) {
target=leftNode.frontSearch(i);
}
if (target==null&rightNode != null) {
target=rightNode.frontSearch(i);
}
}
return target;
}
public void delete(int i){
ThreadedtreeNode parent=this;
if(parent.leftNode!=null&&parent.leftNode.value==i){
this.leftNode=null;
return;
}
if(parent.rightNode!=null&&parent.rightNode.value==i){
this.rightNode=null;
return;
}
parent=leftNode;
if(parent!=null){
parent.delete(i);
}
parent=rightNode;
if (parent!=null){
parent.delete(i);
}
}
}
3.3 二叉树的遍历
public void threadedIterate(){
ThreadedtreeNode node=root;
while (node!=null){
while (node.leftType==0){
node=node.leftNode;
}
System.out.println(node.value);
while (node.rightType==1) {
node=node.rightNode;
System.out.println(node.value);
}
node = node.rightNode;
}
}
4. 赫夫曼树
4.1 什么是赫夫曼树
-
最优二叉树
它是n个带权叶子结点构成的所有二叉树中,带权路径长度最小的二叉树。
-
叶结点的带权路径
从根节点到叶结点经过的结点数x叶子结点的权重
-
树的带权路径长度
所有叶子结点的带权路径和
优秀博客
4.2 赫夫曼树的创建
package hefuman;
public class Node implements Comparable {
int value;
Node left;
Node right;
public Node(int value){
this.value=value;
}
@Override
public int compareTo(Node o) {
return this.value-o.value;
}
}
package hefuman;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.List;
public class Test {
public static void main(String[] args) {
int[] arr = {3, 7, 8, 29, 5, 11, 23, 14};
Node node = creatHefumanTree(arr);
}
public static Node creatHefumanTree(int[] arr) {
//先使用数组中所有的元素创建若干个二叉树(只有一个结点)
List nodes = new ArrayList<>();
for (int value : arr) {
nodes.add(new Node(value));
}
//循环处理
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取出权值最小的两个二叉树
Node left = nodes.get(0);
Node right = nodes.get(1);
//创建新的二叉树
Node parent = new Node(left.value + right.value);
parent.left=left;
parent.right=right;
//把取出的二叉树移除
nodes.remove(left);
nodes.remove(right);
//放入原来的二叉树集合中
nodes.add(parent);
}
System.out.println(nodes);
return null;
}
}
4.3 赫夫曼编码
package hufumanCode;
public class Node implements Comparable {
Byte data;
int weight;
Node left;
Node right;
public Node(Byte data,int weight){
this.data=data;
this.weight=weight;
}
@Override
public int compareTo(Node o) {
return this.weight-o.weight;
}
}
package· hufumanCode;
import java.util.*;
public class TestHufumanCode {
public static void main(String[] args) {
String msg = "can you can a can as a can canner can a can.";
byte[] bytes = msg.getBytes();
//进行赫夫曼编码
hufumanZip(bytes);
}
private static byte[] hufumanZip(byte[] bytes) {
//统计每一个byte出现的次数
List nodes = getNodes(bytes);
//创建一棵赫夫曼树
Node tree = createHufumanTree(nodes);
//System.out.println(tree.weight);
//创建一个赫夫曼编码表
Map huffCodes = getCodes(tree);
//编码
//System.out.println(huffCodes);
//进行赫夫曼编码压缩
byte[] b=zip(bytes,huffCodes);
System.out.println(bytes.length);
System.out.println(b.length);
return null;
}
/**
* 把byte数组转为node集合
*
* @param bytes
* @return
*/
private static List getNodes(byte[] bytes) {
List nodes = new ArrayList<>();
Map counts = new HashMap<>();
//统计每一个byte出现的次数
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
for (Map.Entry entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
/**
* 创建赫夫曼树
*/
private static Node createHufumanTree(List nodes) {
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取出权值最小的两棵树
Node left = nodes.get(0);
Node right = nodes.get(1);
//创建新的树
Node parent = new Node(null, left.weight + right.weight);
parent.left=left;
parent.right=right;
//移除两颗权值最小的树
nodes.remove(left);
nodes.remove(right);
//增加新的树
nodes.add(parent);
}
return nodes.get(0);
}
static StringBuilder sb = new StringBuilder();
static Map huffCodes = new HashMap<>();
private static Map getCodes(Node tree) {
if (tree == null) {
return null;
}
getCodes(tree.left, "0", sb);
getCodes(tree.right, "1", sb);
return huffCodes;
}
private static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
//不是叶结点
if (node.data == null) {
getCodes(node.left, "0", sb2);
getCodes(node.right, "1", sb2);
} else {//如果是叶结点
huffCodes.put(node.data, sb2.toString());
}
}
/**
* 进行赫夫曼编码压缩
* @param bytes
* @param huffCodes
* @return
*/
private static byte[] zip(byte[] bytes,Map huffCodes){
StringBuilder sb=new StringBuilder();
for (byte b:bytes){
sb.append(huffCodes.get(b));
}
System.out.println(sb.toString());
//定义长度
int len;
if(sb.length()%8==0){
len=sb.length()/8;
}else{
len=sb.length()/8+1;
}
byte[] by=new byte[len];
int index=0;
for(int i=0;i 4.4 赫夫曼译码
package hufumanCode;
import java.util.*;
public class TestHufumanCode {
public static void main(String[] args) {
String msg = "yang ting ting is testing her javacode of hufuman.";
byte[] bytes = msg.getBytes();
//进行赫夫曼编码压缩
byte[] b=hufumanZip(bytes);
//使用赫夫曼编码进行解码
byte[] newBytes=decode(huffCodes,b);
//验证
System.out.println(Arrays.toString(bytes));
System.out.println(Arrays.toString(newBytes));
//
System.out.println(new String(newBytes));
}
private static byte[] hufumanZip(byte[] bytes) {
//统计每一个byte出现的次数
List nodes = getNodes(bytes);
//创建一棵赫夫曼树
Node tree = createHufumanTree(nodes);
//System.out.println(tree.weight);
//创建一个赫夫曼编码表
Map huffCodes = getCodes(tree);
//编码
//System.out.println(huffCodes);
//进行赫夫曼编码压缩
byte[] bb=zip(bytes,huffCodes);
return bb;
}
/**
* 把byte数组转为node集合
*
* @param bytes
* @return
*/
private static List getNodes(byte[] bytes) {
List nodes = new ArrayList<>();
Map counts = new HashMap<>();
//统计每一个byte出现的次数
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
for (Map.Entry entry : counts.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
/**
* 创建赫夫曼树
*/
private static Node createHufumanTree(List nodes) {
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取出权值最小的两棵树
Node left = nodes.get(0);
Node right = nodes.get(1);
//创建新的树
Node parent = new Node(null, left.weight + right.weight);
parent.left=left;
parent.right=right;
//移除两颗权值最小的树
nodes.remove(left);
nodes.remove(right);
//增加新的树
nodes.add(parent);
}
return nodes.get(0);
}
static StringBuilder sb = new StringBuilder();
static Map huffCodes = new HashMap<>();
private static Map getCodes(Node tree) {
if (tree == null) {
return null;
}
getCodes(tree.left, "0", sb);
getCodes(tree.right, "1", sb);
return huffCodes;
}
private static void getCodes(Node node, String code, StringBuilder sb) {
StringBuilder sb2 = new StringBuilder(sb);
sb2.append(code);
//不是叶结点
if (node.data == null) {
getCodes(node.left, "0", sb2);
getCodes(node.right, "1", sb2);
} else {//如果是叶结点
huffCodes.put(node.data, sb2.toString());
}
}
/**
* 进行赫夫曼编码压缩
* @param bytes
* @param huffCodes
* @return
*/
private static byte[] zip(byte[] bytes,Map huffCodes){
StringBuilder sb=new StringBuilder();
for (byte b:bytes){
sb.append(huffCodes.get(b));
}
// System.out.println(sb.toString());
//定义长度
int len;
if(sb.length()%8==0){
len=sb.length()/8;
}else{
len=sb.length()/8+1;
}
byte[] by=new byte[len];
int index=0;
for(int i=0;i huffCodes,byte[] bytes){
StringBuilder sb=new StringBuilder();
//把byte数组转化为二进制的字符串
for (int i=0;i map=new HashMap<>();
for (Map.Entry entry:huffCodes.entrySet()){
map.put(entry.getValue(),entry.getKey());
}
List list=new ArrayList<>();
//处理字符串
for (int i=0;i package hufumanCode;
public class Node implements Comparable {
Byte data;
int weight;
Node left;
Node right;
public Node(Byte data,int weight){
this.data=data;
this.weight=weight;
}
@Override
public int compareTo(Node o) {
return this.weight-o.weight;
}
}
5. 二叉排序树(二叉查找树)
5.1 概述
对于二叉树中的任何一个非叶子结点,都要求左子结点比当前节点值小,而右子结点比当前结点值大。
注意:如果是一棵空树,我们也可以认为它是二叉排序树。
5.2 代码实现
- 树的创建
- 树的中序遍历
- 指定值查找元素
- 删除结点
package BinarySortTree;
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
public void add(Node node) {
if (node == null) {
return;
}
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
}
public void mediumShow() {
if (this.left != null) {
this.left.mediumShow();
}
System.out.print(this.value + " ");
if (this.right != null) {
this.right.mediumShow();
}
}
public Node search(int value) {
if (this.value == value) {
return this;
}
if (this.right!= null && this.value < value) {
return this.right.search(value);
}
if (this.left != null && this.value > value) {
return this.left.search(value);
}
return null;
}
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
if (this.value > value && this.left != null) {
return this.left.searchParent(value);
}
if (this.value < value && this.right != null) {
return this.right.searchParent(value);
}
}
return null;
}
}
package BinarySortTree;
public class BinarySortTree {
Node root;
public void add(Node node){
if(root==null){
root=node;
}else{
root.add(node);
}
}
public void mediumShow(){
if(root==null){
return;
}else{
root.mediumShow();
}
}
public Node search(int value){
if(root==null){
return null;
}else{
return root.search(value);
}
}
public void delete(int value){
if(root==null){
return;
}else{
Node target=search(value);
if(target==null){
return;
}
//找到他的父结点
Node parent=searchParent(value);
//删除的结点是叶子结点
if(target.left==null&&target.right==null){
if(target.valuepackage BinarySortTree;
public class Test {
public static void main(String[] args) {
int[] arr={7,3,10,1,12,5,9};
BinarySortTree tree=new BinarySortTree();
//创建一颗二叉树
for(int i=0;i6. AVL树—平衡二叉树
6.1 为什么要用平衡二叉树
二叉搜索树有一个缺点,在插入数据是有序的序列(包括升序和降序),会导致二叉树退化成链表,从而导致在查找,删除,添加时的性能均从O(logN)降低为O(N),这是不能接受的。
比如:

究其原因,是因为二叉搜索树退化成链表的时候,树的高度与节点的个数相等,也就是成正比,所以为了优化这种情况,就出现了具有平衡能力的二叉搜索树,其中AVL树是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1, 因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logN)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。
6.2 平衡二叉树定义
- 对于任何一个结点而言,左子树和右子树的高度差的绝对值不大于1。
- 左子树和右子树也是平衡二叉树。
B树、红黑树都是平衡二叉树。
6.3 平衡二叉树关键问题
6.3.1 如何求树的高度
代码实现
public int height(){
return Math.max(left==null?0:left.height(),right==null?0:right.height())+1;
}
6.3.2 关于树的旋转
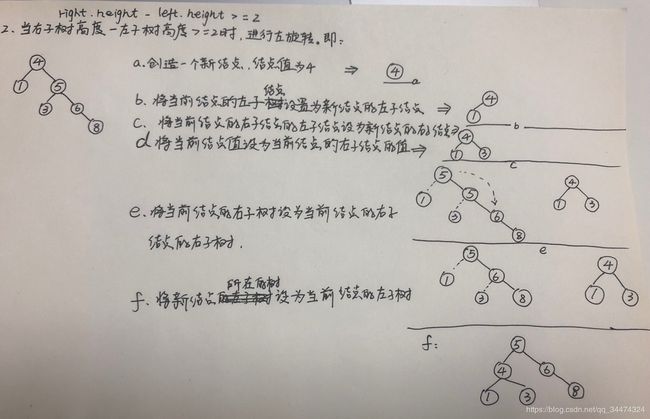
右旋转:
右旋转代码实现:
- 创建一个新结点,结点值为当前结点的值
- 把新结点的右子树设置为当前结点的右子树
- 把新结点的左子树设置为当前结点的左子树的右子树
- 将当前结点的值变为左子结点的值
- 把当前结点的左子树设置为左子结点的左子树
- 将新结点作为当前结点的右子树
if (left!=null&&right!=null&&left.height()-right.height()>=2){
//进行右旋转
rightRotate();
}
//右旋转
public void rightRotate(){
//创建一个新结点,结点值为当前结点的值
Node newNode=new Node(value);
//把新结点的右子树设置为当前结点的右子树
newNode.right=right;
//把新结点的左子树设置为当前结点的左子树的右子树
newNode.left=left.right;
//将当前结点的值变为左子结点的值
value=left.value;
//把当前结点的左子树设置为左子结点的左子树
left=left.left;
//将新结点作为当前结点的右子树
right=newNode;
}
- 创造一个新结点,结点值为当前结点值
- 将当前结点的左子树设为新结点的左子树
- 将当前结点的右子结点的左子树设置为新结点的右子树
- 将当前结点值设置为当前结点的右子结点的值
- 将当前结点的右子树设置为当前结点的右子结点的右子树
- 将新结点所在的树设置为当前结点的左子树
if (left != null && right != null && right.height() - left.height() >= 2) {
//进行左旋转
leftRotate();
}
//左旋转
public void leftRotate(){
//创造一个新结点,结点值为当前结点值
Node newNode=new Node(value);
//将当前结点的左子树设为新结点的左子树
newNode.left=left;
//将当前结点的右子结点的左子树设置为新结点的右子树
newNode.right=right.left;
//将当前结点值设置为当前结点的右子结点的值
value=right.value;
//将当前结点的右子树设置为当前结点的右子结点的右子树
right=right.right;
//将新结点所在的树设置为当前结点的左子树
left=newNode;
}
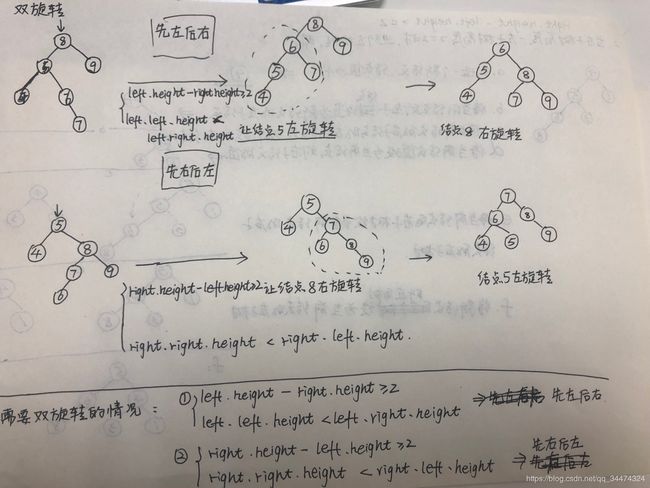
双旋转
6.3.3 小结
6.4 平衡二叉树实现代码
package AvlTree;
public class AvlTree {
Node root;
public void add(Node node){
if(root==null){
root=node;
}else{
root.add(node);
}
}
public void mediumShow(){
if(root==null){
return;
}else{
root.mediumShow();
}
}
public Node search(int value){
if(root==null){
return null;
}else{
return root.search(value);
}
}
/**
* 查找父结点,根结点的父结点不处理
* @param value
* @return
*/
public Node searchParent(int value){
if( root==null){
return null;
}
return root.searchParent(value);
}
}
package AvlTree;
public class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
public void add(Node node) {
if (node == null) {
return;
}
if (node.value < this.value) {
if (this.left == null) {
this.left = node;
} else {
this.left.add(node);
}
} else {
if (this.right == null) {
this.right = node;
} else {
this.right.add(node);
}
}
//查询是否平衡
if (left != null && right != null && left.height() - right.height() >= 2) {
//进行右旋转
//先左旋后右旋
if(left.left!=null&left.right!=null&&left.left.height()= 2) {
//进行左旋转
//先右后左
if(right.left!=null&right.right!=null&&right.right.height() value) {
return this.left.search(value);
}
return null;
}
public Node searchParent(int value) {
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
if (this.value > value && this.left != null) {
return this.left.searchParent(value);
}
if (this.value < value && this.right != null) {
return this.right.searchParent(value);
}
}
return null;
}
//求树的高度
public int height(){
return Math.max(left==null?0:left.height(),right==null?0:right.height())+1;
}
//右旋转
public void rightRotate(){
//创建一个新结点,结点值为当前结点的值
Node newNode=new Node(value);
//把新结点的右子树设置为当前结点的右子树
newNode.right=right;
//把新结点的左子树设置为当前结点的左子树的右子树
newNode.left=left.right;
//将当前结点的值变为左子结点的值
value=left.value;
//把当前结点的左子树设置为左子结点的左子树
left=left.left;
//将新结点作为当前结点的右子树
right=newNode;
}
//左旋转
public void leftRotate(){
//创造一个新结点,结点值为当前结点值
Node newNode=new Node(value);
//将当前结点的左子树设为新结点的左子树
newNode.left=left;
//将当前结点的右子结点的左子树设置为新结点的右子树
newNode.right=right.left;
//将当前结点值设置为当前结点的右子结点的值
value=right.value;
//将当前结点的右子树设置为当前结点的右子结点的右子树
right=right.right;
//将新结点所在的树设置为当前结点的左子树
left=newNode;
}
}
package AvlTree;
public class Test {
public static void main(String[] args) {
int[] arr={5,4,8,7,9,6};
AvlTree tree=new AvlTree();
//创建一颗二叉树
for(int i=0;i7. 多路查找树
增加每个结点存放元素的个数,以减少树的高度,提高计算机访问硬盘速度。
7.1 计算机存储方式
7.1.1硬盘
固态硬盘跟机械硬盘都是怎么储存数据的
揭开固态硬盘的神秘面纱,一张图看懂机械硬盘和固态硬盘的区别!
硬盘结构(机械硬盘和固态硬盘)详解
7.1.2 内存
优点: 使用电信号来保存信息,不存在机器操作,所以访问速度非常快。
缺点: 造价高,断电后数据容易丢失,一般作为CPU的高速缓存。
7.2 2-3树—B树的一种特例
- B树中所有的叶子结点都在同一层。
- 有两个子结点的结点叫二结点,有三个子结点的结点叫三结点。
- 二结点要么有两个子结点,要么没有子结点;三结点要么有三个子结点,要么没有子结点。
7.3 2-3-4树
- B树中所有的叶子结点都在同一层。
- 有两个子结点的结点叫二结点,有三个子结点的结点叫三结点,有四个子结点的结点叫四结点。
- 二结点要么有两个子结点,要么没有子结点;三结点要么有三个子结点,要么没有子结点;四结点要么有四个子结点,要么没有子结点。
7.4 B树
- B树的阶
- B+树:非叶子结点只存储索引信息,不存储数据;叶子结点最右边的指针指向下一个相邻的叶结点。
- 所有的叶结点组成了一个有序链表。