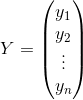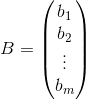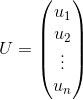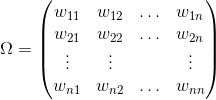广义最小二乘法的证明

需用到的知识：

1）正交矩阵：

     如果（为单位矩阵，表示“矩阵A的转置矩阵”）或，则n阶实矩阵称为正交矩阵。

    根据这个定义，很容易得到的是，也就是说正交矩阵的逆很容易求，直接对原矩阵转置就是原矩阵的逆。

    显然非常容易推出下面的一个定理：

    A是n阶实正交矩阵，B也是n阶实正交矩阵，那么AB仍然是n阶实正交矩阵。

    证明：

   根据正交矩阵的定义，如果证明，那就证明了也是正交矩阵。

    因为A是正交矩阵，所以，

    因为B是正交矩阵，所以.

   所以，。

   证明毕。

2）实对称矩阵：

   因为是对称矩阵，所以如果A是实对称矩阵，那么肯定满足：

    实对称矩阵的定理1：实对称矩阵的特征值必为实数。

    实对称矩阵的定理2：实对称矩阵的不同特征值所对应的特征向量正交。

    实对称矩阵的定理3:  设为n阶实对称矩阵，则必有正交矩阵, 使得，其中是以的n个特征值为对角元素的对角矩阵。

   这里证明定理3，其他两个定理网上比较容易找到证明，并且他们的证明也比较容易理解。

   定理3的证明来自：https://wenku.baidu.com/view/713224a1f021dd36a32d7375a417866fb84ac064.html?from=search

   证明如下（采用数学归纳法）：

    当时，定理显然成立。

    然后，根据归纳法原理，现在假设n-1阶实对称矩阵来说定理是成立的，那么只要证明在此基础上，n阶实对称矩阵也成立，那么整个定理就得到证明。

    假设是n阶对称矩阵A的一个特征值（这里的假设是合理的，因为实对称矩阵的定理1），是属于特征值的特征向量，显然很容易就可以把进行单位化，单位化后的向量，显然，向量仍然是特征值的特征向量。为形成正交化矩阵，我们可以直接假设向量是单位化之后的向量。我们记是以为第一列任意正交矩阵。把分块为，其中为矩阵。

则

注意到

   

 

以及，与的各列向量都正交，所以

其中为阶实对称矩阵。

根据归纳法假设，n-1阶实对称矩阵是存在一个n-1阶正交矩阵使得：

令, ，

则，均为n阶正交矩阵（理论依据参考本文1)部分内容），并且

这表明为对角矩阵。根据数学归纳法原理，对任意n阶实对称矩阵定理3结论成立。

3）实对称矩阵的一个推论

根据上面实对称矩阵的定理3，我们可以有这么一个推论，就是：

任何n阶实对称矩阵A，都可以分解为某个n阶方阵P乘以P的转置，即。这里的P是复数域的。

证明：

由实对称矩阵的定理3可知，始终存在一个正交矩阵Q使得A可以对角化，即：

因此有:

如果令

(注意，如果是负数，那么就是虚数，因此允许是复数域的，另外比较明显的是这个P在复数域是可逆的，很容易可以得出)

所以，。

证明毕。

3）广义最小二乘法

这部分来自：https://wenku.baidu.com/view/9ede2058876fb84ae45c3b3567ec102de2bddfaa.html

普通最小二乘法、加权最小二乘法是广义最小二乘法的特例。

存在序列相关性最常用的方法是广义最小二乘法

             

假设

 ，

因此， 

   可以是异方差的(也就是对角线上至少存在一对和是不相等的)。

设,(这个假设是合理的，因为是一个实对称矩阵，上面已经有推论，在复数域上是可以分解为的)。

用左乘两边

即

     (这一步的理由: )

再用普通最小二乘法得：

这就是广义最小二乘法估计模型的参数估计量。

矩阵的估计为