Manacher’s Algorithm超详细！！！

0x00 问题描述

给定一个字符串，找到最长的回文子串。

• 如果给定的字符串是“forgeeksskeegfor”，则输出应为“geeksskeeg”
• 如果给定的字符串是“abaaba”，则输出应为“abaaba”
• 如果给定的字符串是“abababa”，则输出应为“abababa”
• 如果给定的字符串是“abcbabcbabcba”，则输出应为“abcbabcba”

0x01 常见解法

寻找回文的一种方法是从字符串的中心开始，逐个比较左右两个方向上的字符。如果两侧（中心的左侧和右侧）的相应字符匹配，那么它们将成为回文。举个例子，对于字符串“abababa”。

这里字符串的中心是第4个字符（索引3）b。如果我们匹配中心左右两侧的字符，则所有字符都匹配，因此字符串“abababa”是回文。

这里的中心位置不仅是实际的字符串字符位置，而且也可以是两个字符之间的位置。考虑偶数长度的字符串“abaaba”。 该字符串中心在第3和第4个字符a和a之间。

要找到长度为$N$的字符串的最长回文子串，一种方法是取每个可能的$2N+1$个中心（$N$个字符位置，两个字符之间的$N-1$个位置和左右两个边界位置），对于每个中心，分别从左右方向上匹配字符并跟踪LPS。 这种方法时间复杂度是$O(N^2)$。

0x02 Manacher 算法

让我们考虑两个字符串“abababa”和“abaaba”

在这两个字符串中，中心位置（第一字符串中的位置7和第二字符串中的位置6）的左侧和右侧是对称的。为什么？因为整个字符串是围绕中心位置的回文串。

如果我们需要从左到右计算每个$2N+1$个位置的最长回文子串，那么回文的对称性可以帮助避免一些不必要的计算（即字符比较）。如果在任何位置$P$都有一些长度为$L$的回文，那么我们可能不需要在位置$P+1$处比较左侧和右侧的所有字符。我们已经在$P$之前的位置计算了LPS，它们可以帮助避免位置$P$之后的一些比较。

我们来看看字符串“abababa”，它有15个中心位置。我们需要计算每个位置的最长回文串的长度。

• 在位置0处，根本没有LPS（左侧没有要比较的字符），因此LPS的长度将为0。

• 在位置1处，LPS是a，因此LPS的长度将为1。

• 在位置2处，根本没有LPS（左和右字符a和b不匹配），因此LPS的长度将为0。

• 在位置3处，LPS是aba，因此LPS的长度将是3。

• 在位置4处，根本没有LPS（左和右字符b和a不匹配），因此LPS的长度将为0。

• 在位置5处，LPS是ababa，因此LPS的长度为5。

  … 等等。

我们将所有这些回文长度存储在一个数组中，比如说$L$。然后字符串S和LPS长度$L$如下所示：

同样，字符串“abaaba”的LPS长度$L$将如下所示：

在LPS阵列中：

• 奇数位置（实际字符位置）的LPS长度值将为奇数且大于或等于1（如果在其左侧和右侧没有其他匹配项，则1将来自中心字符本身）
• 偶数位置的LPS长度值（两个字符之间的位置，最左侧和右侧位置）将是偶数且大于或等于$0$（当左侧和右侧没有匹配时将出现$0$）

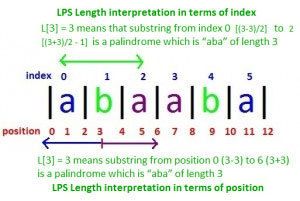
字符串的位置和索引是两个不同的东西。对于长度为$N$的给定字符串$S$，索引将是从$0$到$N-1$（总$N$个索引），并且位置将是从$0$到$2N$（总共$2N+1$个位置）。

LPS长度值可以用两种方式解释，一种是索引，另一种是位置。位置$I$处的LPS值$d$（$L[i]=d$）表示：

• 从位置$i-d$到$i+d$的子串是长度为$d$的回文（就位置而言）
• 从索引$(i-d)/2$到$[(i+d)/2-1]$的子串是长度为d的回文（就索引而言）

例如在字符串“abaaba”中，$L[3]=3$表示从位置$0$（$3-3$）到$6$（$3+3$）长度为$3$的回文子字符串“aba”，它也可以表示为索引$0$$[(3-3)/2]$至$2[(3+3)/2-1]$长度为$3$的的回文子字符串“aba”。现在主要任务是怎么有效地计算LPS数组。 一旦计算出该数组，字符串$S$的LPS将是以LPS数组中最大LPS长度值的位置为中心。

0x0201 计算LPS数组

为了有效地计算LPS数组，我们需要解决的问题就是后面需要计算LPS长度的位置如何与先前已经计算LPS长度的位置相关联。

对于字符串“abaaba”：

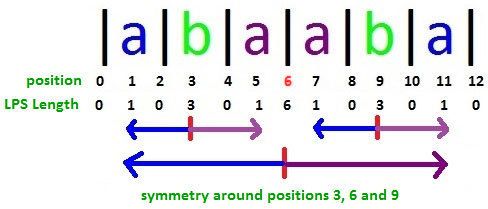
当我们计算到第$3$个位置：

• 位置$2$和位置$4$处的LPS长度值相同
• 位置$1$和位置$5$处的LPS长度值相同

我们从位置$0$开始从左到右计算LPS长度值，因此我们已经知道位置$1$，$2$和$3$处的LPS长度值，那么我们就不需要计算位置$4$和$5$处的LPS长度，因为它们是等于位置3左侧相应位置的LPS长度值。

当我们计算到第$6$个位置：

• 位置$5$和位置$7$处的LPS长度值相同

• 位置$4$和位置$8$处的LPS长度值相同

  …等等。

如果我们已经知道位置$1,2,3,4,5$和$6$处的LPS长度值，那么我们就不需要计算位置$7,8,9,10$和$11$处的LPS长度，因为它们等于位置$6$左侧相应位置的LPS长度值。

接着考虑字符串“abababa”：

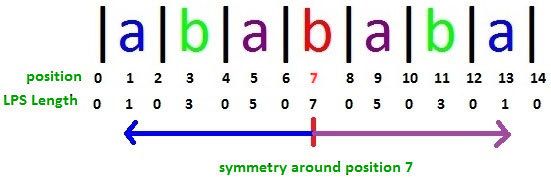
如果我们已经知道位置$1,2,3,4,5,6$和$7$处的LPS长度值，那么我们就不需要计算位置$8,9,10,11,12$和$13$处的LPS长度，因为它们等于位置$7$左侧相应位置的LPS长度值。

你能看出为什么在字符串“abaaba”中的位置$3,6,9$周围的LPS长度值是对称的吗？那是因为这些位置周围有一个回文子串。对于字符串“abababa”在$7$这个中心位置也是如此。

在回文串中心位置附近的LPS长度值是否总是对称的（相同）？答案是否定的。

我们看字符串“abababa”中的位置$3$和$11$，两个位置都具有LPS长度$3$。但是位置$1$和$5$（位置$3$两侧）不对称。类似地，位置$9$和$13$（位置$11$两侧）不对称。

此时，我们可以看到，在以某个位置为中心的回文串左右，围绕中心位置的LPS长度值可能对称也可能不对称。如果我们能够知道什么时候左右位置的LPS长度是对称，我们就可以不用计算右侧位置的LPS长度，因为它将与已知的左侧相应位置的LPS值完全相同。

0x0202 参数

让我们先介绍一些术语：

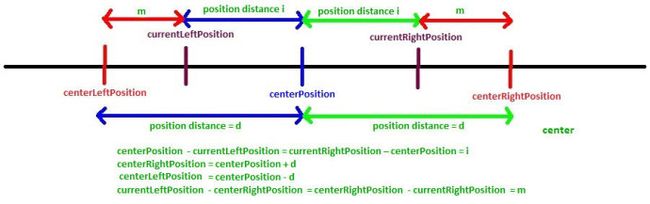
• centerPosition - 这是计算LPS长度的起始位置，假设centerPosition的LPS长度为d（即L [centerPosition] = d）

• centerRightPosition - 距离centerPosition右侧长度d（即centerRightPosition = centerPosition + d）

• centerLeftPosition - 距离centerPosition的左侧长度d（即centerLeftPosition = centerPosition - d）

• currentRightPosition - 这是centerPosition右侧的位置，LPS长度未知

• currentLeftPosition - 这是centerPosition左侧的位置，对应于currentRightPosition

  centerPosition - currentLeftPosition = currentRightPosition - centerPosition

  currentLeftPosition = 2*centerPosition - currentRightPosition

• i-left palindrome - 位于centerPosition的左侧，以currentLeftPosition为中心的回文串

• i-right palindrome - 位于centerPosition的右边，以currentRightPosition为中心的回文串

• center palindrome - 以centerPosition为中心的回文串

假设我们处于已知LPS长度的centerPosition，并且同时我们知道所有小于centerPosition位置的LPS长度。假设此时centerPosition的LPS长度为$d$，即L[centerPosition] = d，这意味着位置centerPosition-d到centerPosition+d之间的子串是一个回文串。现在我们继续计算大于centerPosition位置的LPS长度。假设我们在currentRightPosition（> centerPosition），我们需要知道此处的LPS长度。为此，我们查看已计算的currentLeftPosition的LPS长度。如果currentLeftPosition的LPS长度小于centerRightPosition - currentRightPosition，则currentRightPosition的LPS长度将等于currentLeftPosition的LPS长度。这是第一种情况。

让我们考虑字符串“abababa”d：

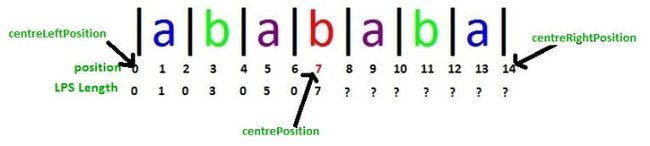
当我们计算到位置7的LPS长度时，其中L[7]=7，如果我们将位置7视为centerPosition，则centerLeftPosition将为0并且centerRightPosition将为14。现在我们需要计算centerPosition右侧其它位置的LPS长度。对于currentRightPosition=8，currentLeftPosition为6并且L[currentLeftPosition]=0，centerRightPosition - currentRightPosition = 14 - 8 = 6，恰好是第一种情况，因此L[currentRightPosition] = L[8] = 0。对于第10和第12位同样适用，因此，L[10] = L[4] = 0、L[12] = L[2] = 0。如果我们看第9位，那么currentRightPosition=9，centerRightPosition - currentRightPosition = 14 - 9 = 5，这里L[currentLeftPosition] = centerRightPosition - currentRightPosition，所以第一种情况不适用于此处。另外要注意的是，centerRightPosition是输入字符串的结束位置，这意味着中心回文串是输入字符串的后缀。在这种情况下，L[currentRightPosition] = L[currentLeftPosition]。这就是第二种情况。

第$9,11,13$和$14$号位置适用于第二种情况，因此：L[9] = L[5] = 5、L[11] = L[3] = 3、L[13] = L[1] = 1、L[14] = L[0] = 0

第一种和第二种情况本质的不同是什么？当一个较大长度的回文串结构包含一个位于其自身中心左侧的较小长度回文串时，那么基于对称性质，将会有另一个相同的较小长度的回文串位于较大长度的回文串的右侧。如果左侧的较小回文串不是较大回文串的前缀，则是第一种情况，如果它是前缀并且较大回文串是输入字符串本身的后缀，则是第二种情况。

如果当前的中心回文串（center palindrome）完全包含左侧回文串并且左侧回文串不是中心回文串的前缀（第一种情况）或（如果我左回文是中心回文的前缀）如果中心回文串是整个字符串的后缀（第二种情况），那么在当前中心右侧（i-right palindrome）的最长回文串与当前中心（i-left palindrome）左侧的最长回文串一样长。为什么呢？

左侧回文串不能比相应的右侧回文串更长，这个很好理解，因为右边是从左边得到的。那么为什么右侧回文串不能比左侧回文串更长呢？

我们举个例子

当centerPosition=11，那么centerLeftPosition=11 - 9 = 2，centerRightPosition=11 + 9=20，如果我们此时currentRightPosition=15，那么它的currentLeftPosition=7。恰好是第一种情况，因此L[15]=3。以位置7为中心的左侧回文串是“bab”，它完全包含在以位置11为中心的中心回文串中（“dbabcbabd”）。我们可以看到右侧回文串不可能比左侧回文串更长，因为如果右边扩张了，由于中心回文串的对称性，左边势必会扩张，最后的结果就是左边回文串成为了中心回文串的前缀（这与前提不符）。所以由于对称性，左侧回文串将与右侧回文串完全相同，这使得第一种情况下L[currentRightPosition] = L[currentLeftPosition]。

现在，如果我们考虑centerPosition=19，那么centerLeftPosition=12和centerRightPosition=26。如果此时currentRightPosition=23，那么currentLeftPosition=15。恰好是第二种情况，因此L[23] = 3。以位置15为中心的左侧回文串是“bab”，它完全包含在以位置19为中心的中心回文串中（“babdbab”）。在第二种情况中，左侧回文串是中心回文串的前缀，右侧回文串的长度不可能超过左侧回文串，因为中心回文串是输入字符串的后缀，因此没有更多的字符可供比较和扩展。这使得第二种情况下L[currentRightPosition] = L[currentLeftPosition]。

0x0203 不同情况分类

情况1：L[currentRightPosition] = L[currentLeftPosition] 适用条件：

• 左侧回文串完全包含在中心回文中

• 左侧回文串不是中心回文串的前缀

当L[currentLeftPosition] < centerRightPosition - currentRightPosition时，上面两个条件成立。

情况2：L[currentRightPosition] = L[currentLeftPosition]适用条件：

• 左侧回文串是中心回文串的前缀（也意味着完全包含）
• 中心回文串是输入字符串的后缀

L[currentLeftPosition] = centerRightPosition - currentRightPosition（对应第一个条件）并且centerRightPosition = 2*N，其中N是输入字符串长度（对应第二个条件）。

情况3：L[currentRightPosition] >= L[currentLeftPosition]适用条件：

• 左侧回文串是中心回文串的前缀（也意味着完全包含）
• 中心回文串不是输入字符串的后缀

L[currentLeftPosition] = centerRightPosition - currentRightPosition（对应第一个条件）并且
centerRightPosition < 2*N，其中N是输入字符串长度N（对应第二个条件）。在这种情况下，有可能出现右侧回文扩张，因此右侧回文串的长度至少与左侧回文串的长度一样长。

情况4：L[currentRightPosition]> centerRightPosition - currentRightPosition适用条件：

• 左侧回文串并非完全包含在中心回文中

当L[currentLeftPosition] >= centerRightPosition - currentRightPosition时，上述条件成立。在这种情况下，左侧回文串的长度至少与（centerRightPosition-currentRightPosition）一样长，并且有可能出现右侧回文回文扩展。

在下图中，

如果我们取centerPosition=7，则情况3适用于currentRightPosition=11时，因为currentLeftPosition=3处的左侧回文串是中心回文串的前缀而右侧回文串不是输入字符串的后缀，所以这里L[11] = 9，大于左侧回文串的长度L[3] = 3。在这种情况下，保证L[11]至少为3，所以在实现中，我们首先设置L[11] = 3，然后我们尝试比较以位置11中心距离为4的左侧和右侧的字符来扩展它。

如果我们取centerPosition=11，则情况4适用于currentRightPosition=15时，因为L[currentLeftPosition] = L[7] = 7 > centerRightPosition - currentRightPosition = 20 - 15 = 5。在这种情况下，保证L[15]将至少为5，所以在实现中，我们首先设置L[15] = 5，然后我们尝试比较以位置15为中心距离为5的左侧和右侧的字符来扩展它。

如果以currentRightPosition为中心的回文扩展超出centerRightPosition，我们将centerPosition更改为currentRightPosition。现在剩下要讨论的一点是，当我们在一个中心位置计算完不同rightPositions的LPS长度时，如何知道下一个中心位置是什么？

0x03 示例

我们已经知道在第一种情况和第二种情况中不需要新的字符比较。在第三种情况和第四种情况中，需要进行必要的比较。

在下图中，

如果我们需要比较，我们只会比较实际字符（也就是|不比较），它们处于“奇数”位置，如$1,3,5,7$等。如果不同奇数位置的两个字符匹配，则它们将LPS长度增加2。

如果采用偶数和奇数位置的处理方式，有很多方法可以实现这一点。一种方法是创建一个新的字符串，我们在所有偶数位置插入一些独特的字符（比如＃，$ 等），然后在其上运行算法（以避免偶数和奇数位置处理的不同方式）。

在这里，我们以给定的字符串为例。当需要进行字符比较时，我们将逐个扩展左右两个位置。当找到奇数位置时，将进行比较并且LPS长度将增加1。当找到偶数位置时，不进行比较并且LPS长度将增加1（因此总体而言，左侧和右侧的一个奇数位置和一个偶数位置将使LPS长度增加两倍）。

我们再次回顾前面说的四种情况，所有四种情况都取决于currentLeftPosition（L[iMirror]）的LPS长度值和（centerRightPosition - currentRightPosition）的值，即（R-i）。 越早知道这两个信息就越有助于我们重用以前的可用信息，这样就可以避免不必要的字符比较。

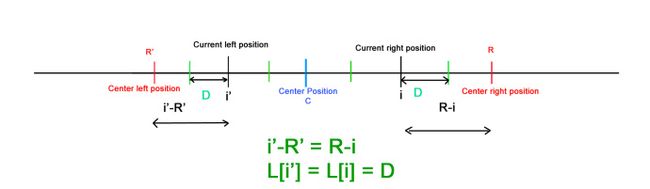
对于所有的四种情况，我们都可以将L[iMirror]和R-i的最小值设置为L[i]，然后我们尝试在任何可扩展的情况下扩展回文。

def findLongestPalindromicString(text): 
    N = len(text) 
    if N == 0: 
        return
    N = 2*N+1    # Position count 
    L = [0] * N 
    L[0] = 0
    L[1] = 1
    C = 1     # centerPosition 
    R = 2     # centerRightPosition 
    i = 0    # currentRightPosition 
    iMirror = 0     # currentLeftPosition 
    maxLPSLength = 0
    maxLPSCenterPosition = 0
    start = -1
    end = -1
    diff = -1
   
    # Uncomment it to print LPS Length array 
    # printf("%d %d ", L[0], L[1]); 
    for i in range(2,N): 
       
        # get currentLeftPosition iMirror for currentRightPosition i 
        iMirror = 2*C-i 
        L[i] = 0
        diff = R - i 
        # If currentRightPosition i is within centerRightPosition R 
        if diff > 0: 
            L[i] = min(L[iMirror], diff) 
   
        # Attempt to expand palindrome centered at currentRightPosition i 
        # Here for odd positions, we compare characters and 
        # if match then increment LPS Length by ONE 
        # If even position, we just increment LPS by ONE without 
        # any character comparison 
        try: 
            while ((i + L[i]) < N and (i - L[i]) > 0) and \ 
                    (((i + L[i] + 1) % 2 == 0) or \ 
                    (text[(i + L[i] + 1) // 2] == text[(i - L[i] - 1) // 2])): 
                L[i]+=1
        except Exception as e: 
            pass
   
        if L[i] > maxLPSLength:        # Track maxLPSLength 
            maxLPSLength = L[i] 
            maxLPSCenterPosition = i 
   
        # If palindrome centered at currentRightPosition i 
        # expand beyond centerRightPosition R, 
        # adjust centerPosition C based on expanded palindrome. 
        if i + L[i] > R: 
            C = i 
            R = i + L[i] 
   
    # Uncomment it to print LPS Length array 
    # printf("%d ", L[i]); 
    start = (maxLPSCenterPosition - maxLPSLength) // 2
    end = start + maxLPSLength - 1
    print("LPS of string is " + text + " : " + text[start:end+1])

如有问题，希望大家指出！！！

reference:

https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-1/

https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-2/

https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-3-2/

https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-4/