b树索引及其变种
b树索引及其变种
1. b-tree
在计算机科学中,B树(英语:B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。B树,概括来说是一个一般化的二叉查找树(binary search tree),可以拥有多于2个子节点。与自平衡二叉查找树不同,B树为系统大块数据的读写操作做了优化。B树减少定位记录时所经历的中间过程,从而加快存取速度。B树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
其主要特点在于可以拥有多于2个子节点。
其定义如下:
- 根结点的儿子数为[2, M];
- 除根结点以外的非叶子结点的儿子数为[M/2, M];(M>2)
- 每个结点存放至少M/2-1(取上整)和至多M-1个关键字(时间为键值对);
- 非叶子结点的关键字个数=指向儿子的指针个数-1;
- 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
- 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
- 所有叶子结点位于同一层;
2. b+tree
B+树是B-树的变体,也是一种多路搜索树,其定义基本与B-树同,除了:
- 非叶子结点的子树指针与关键字个数相同;非叶节点关键字,只作为索引
- 非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树(B-树是开区间);
- 为所有叶子结点增加一个链指针;
- 所有关键字都在叶子结点出现。
3. b*tree
是B+树的变体。
- 在B+树的非根和非叶子结点再增加指向兄弟的指针;
- B*树定义了非叶子结点关键字个数至少为(2/3)xM,即块的最低使用率为2/3(代替B+树的1/2);
4. b-link tree(Lehman/Yao)
- take a B±tree (they call it a B*-tree)
- add “high keys” to each page
- add right-links to each page (Idea: think of two nodes with a right-link as one big node)
- ensure that people search top-down, left-to-right
- ensure that people insert bottom-up
- Requires NO locking for read (!!)
- “Lock coupling” for writes is rare (question: why is lock coupling so bad?)
作为b*树的变种,其在每个page上添加了high key用来标识此页上的最大值。同时每个page添加了指向其兄弟节点的链接。
Compared to a classic B-tree, L&Y adds a right-link pointer to each page,
to the page’s right sibling. It also adds a “high key” to each page, which
is an upper bound on the keys that are allowed on that page. These two
additions make it possible detect a concurrent page split, which allows the
tree to be searched without holding any read locks (except to keep a single
page from being modified while reading it).When a search follows a downlink to a child page, it compares the page’s
high key with the search key. If the search key is greater than the high
key, the page must’ve been split concurrently, and you must follow the
right-link to find the new page containing the key range you’re looking
for. This might need to be repeated, if the page has been split more than
once.
其主要思想是只对需操作节点加锁,操作完(读或写)解锁,减少加锁,那么必然会存在一个事务读取了页节点指针后解锁,另一事务在split页节点后,导致数据在其右节点。因此通过添加指向右兄弟节点的指针来找到正确数据位置。
Lehman/Yao的b-link tree 不会删除非页节点上数据,当树上数据太少通过reorganization.
A simple way of handling deletions is to allow fewer than K entries in a leaf node. This is unnecessary for nonleaf nodes, since deletion only removes keys from a leaf node; a key in a nonleaf node only serves as an upper bound for its associated pointer; it is not removed during deletion.
It uses very little extra storage under the as- sumption that insertions take place more often than deletions. In situations where excessive deletions cause the storage utilization of tree nodes to be unacceptably low, a batch reorganization or an underflow operation which locks the entire tree can be performed.
4.1 search
查找时不加锁,读操作为原子操作。
/*from disk*/
current = root; //获取root指针,从root开始 top-down
page = get(current); //获取当前页(从磁盘读)
//找到leaf
while (current is not a leaf) {
current = scannode(value, page); //在当前页查找记录v,非页节点获得下一page地址
page = get(current);
}
//在leaf节点查找value,若获得兄弟节点指针,则再次获得兄弟节点page
while ((t = scannode(value,page)) == link pointer of A) {
current = t;
page = get(current);
}
//在page查找value,找到,成功,没找到,则无此数据
if (v is in page)
return(success);
else return(failure);
/*from memory 与disk区别,不需从disk读page到内存*/
current = root; //获取root指针
//找到leaf
while (current is not a leaf) {
current = scannode(value, current); //在当前页查找记录v,非页节点获得下一page地址
}
//在leaf节点查找value,若获得兄弟节点指针,则再次获得兄弟节点page
while ((t = scannode(value,current)) == link pointer of A) {
current = t;
}
//在page查找value,找到,成功,没找到,则无此数据
if (v is in current)
return(success);
else return(failure);
4.2 insert
/* disk */
if pageA is safe {
insert new key/ptr pair on page;
put(page, current);
unlock(current);
}
else { // gonna have to split
u = allocate(1 new page for pageB);
redistribute pageA over pageA and pageB;
y = max value on pageA now;
make high key of pageB equal old high key of pageA;
make right-link of pageB equal old right-link of pageA;
make high key of pageA equal y;
make right-link of pageA point to pageB;
put (pageB, u);
put (pageA, current);
oldnode = current;
new key/ptr pair = (y, u); // high key of new page, new page
current = pop(stack); // get parent
lock(current); //lock parent
pageA = get(current);
move_right(); // at this point we may have 3 locks: oldnode, and two at the parent level while moving right **在加right锁后,释放current**
unlock(oldnode); //unlock current
goto Doinsertion; //在parent插入
}
4.3 delete
Just remove from the leaf. They put on underflow – just let leaves get empty, never delete them (hence never do deletion from internal nodes.) If you think your tree is too empty, then reorganize it offline. In practice, people don’t deal with underflow in real systems, but do reclaim empty pages periodically.
在Efficient Locking for Concurrent Operations on B-Trees一文中,描述了一种简单的删除方法,即并不对树进行合并,在删除时只是简单的删除leaf中数据,直到为空,同时也不会去删除非页节点数据;通过offline的reorganize处理empty,或者定时清理。
live lock
在某些特殊情况下,查找会一直查找右节点。
5. b-link tree(Vladimir Lanin and Dennis Shasha)
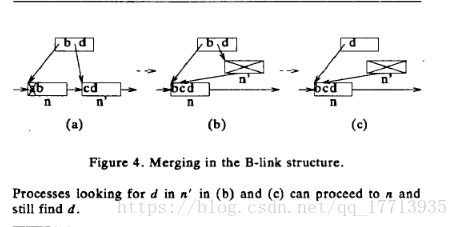
V. Lanin and D. Shasha 的b-link tree 在 Lehman/Yao 的基础上修改了delete操作,实现了在delete时merge page。**其他也有一些修改比如读加锁,读完一个节点解锁等。**下面主要介绍其delete(merge)操作。
delete(merge)
添加outlink指向左节点。
A,B merge(c为B的right link),对A,B加锁,把B数据移到A中,B的outlink指向A,A的right link指向C,释放B,释放A,删除父节点中的指向B的down link和A的high key (加锁操作)。
- 对父节点进行删除操作为异步操作。
- 同时最多对两节点加锁。
- 如果merge的两个节点其父节点不为同一个先对其进行merge(在论文中介绍的一种方法)
4.4 pgsql 实现
代码位置src/backend/access/nbtree
其中README介绍了其为了适配pgsql对b-link tree(Lehman/Yao)的修改。
search
以下是postgresql中b-link three的部分search实现
_bt_search:
/* 获取root page,Get the root page to start with */
*bufP = _bt_getroot(rel, access);
......
for(;;)
/* 看是否需获取兄弟节点,并做些处理 要获取兄弟节点,释放本节点锁,获取下一节点锁*/
*bufP = _bt_moveright
/* if this is a leaf page, we're done */
page = BufferGetPage(*bufP); //获取page
opaque = (BTPageOpaque) PageGetSpecialPointer(page);
if (P_ISLEAF(opaque)) // 如果是叶子节点查找结束
break;
/*
* Find the appropriate item on the internal page, and get the child
* page that it points to.
*/
offnum = _bt_binsrch(rel, *bufP, keysz, scankey, nextkey); // 二分查找非叶节点中指向下一节点的对应项
// 父节点入栈
/* save stack */
new_stack = (BTStack) palloc(sizeof(BTStackData));
new_stack->bts_blkno = par_blkno;
new_stack->bts_offset = offnum;
memcpy(&new_stack->bts_btentry, itup, sizeof(IndexTupleData));
new_stack->bts_parent = stack_in;
/* drop the read lock on the parent page, acquire one on the child */
*bufP = _bt_relandgetbuf(rel, *bufP, blkno, BT_READ);
/* 开始下一层 */
_bt_moveright:
insert
postgresql insert:
_bt_doinsert:
/* find the first page containing this key */
stack = _bt_search(rel, natts, itup_scankey, false, &buf, BT_WRITE, NULL);
/* trade in our read lock for a write lock 读锁转写锁*/
LockBuffer(buf, BUFFER_LOCK_UNLOCK);
LockBuffer(buf, BT_WRITE);
buf = _bt_moveright(rel, buf, natts, itup_scankey, false,true, stack, BT_WRITE, NULL);//由于上面放过锁,可能节点已分裂,moveright
//是否检测建冲突
if (checkUnique != UNIQUE_CHECK_NO)
// 检测键冲突
offset = _bt_binsrch(rel, buf, natts, itup_scankey, false);
xwait = _bt_check_unique(rel, itup, heapRel, buf, offset, itup_scankey,checkUnique, &is_unique, &speculativeToken);
// 是否只需检测键冲突,不插数据
if (checkUnique != UNIQUE_CHECK_EXISTING)
// 插入
/* do the insertion */
_bt_findinsertloc(rel, &buf, &offset, natts, itup_scankey, itup, stack, heapRel);// 找到要插入的位置,如果page满,且插入值==high key,往右查找free page,查找有限次
_bt_insertonpg(rel, buf, InvalidBuffer, stack, itup, offset, false);
/*
* bt_findinsertloc() -- Finds an insert location for a tuple
*
* If the new key is equal to one or more existing keys, we can
* legitimately place it anywhere in the series of equal keys --- in fact,
* if the new key is equal to the page's "high key" we can place it on
* the next page. If it is equal to the high key, and there's not room
* to insert the new tuple on the current page without splitting, then
* we can move right hoping to find more free space and avoid a split.
* (We should not move right indefinitely, however, since that leads to
* O(N^2) insertion behavior in the presence of many equal keys.)
* Once we have chosen the page to put the key on, we'll insert it before
* any existing equal keys because of the way _bt_binsrch() works.
*
* If there's not enough room in the space, we try to make room by
* removing any LP_DEAD tuples.
*
* On entry, *bufptr and *offsetptr point to the first legal position
* where the new tuple could be inserted. The caller should hold an
* exclusive lock on *bufptr. *offsetptr can also be set to
* InvalidOffsetNumber, in which case the function will search for the
* right location within the page if needed. On exit, they point to the
* chosen insert location. If _bt_findinsertloc decides to move right,
* the lock and pin on the original page will be released and the new
* page returned to the caller is exclusively locked instead.
*
* newtup is the new tuple we're inserting, and scankey is an insertion
* type scan key for it.
*/
_bt_insertonpg:
// 是否需split ,在bt_findinsertloc已查找过尽量不需split的叶
if (PageGetFreeSpace(page) < itemsz)
/* 查找split点 Choose the split point */
firstright = _bt_findsplitloc(rel, page, newitemoff, itemsz,&newitemonleft);
/* 分裂页 split the buffer into left and right halves */
rbuf = _bt_split(rel, buf, cbuf, firstright,newitemoff, itemsz, itup, newitemonleft);
PredicateLockPageSplit(rel,BufferGetBlockNumber(buf),BufferGetBlockNumber(rbuf));
/*----------
* By here,
*
* + our target page has been split;
* + the original tuple has been inserted;
* + we have write locks on both the old (left half)
* and new (right half) buffers, after the split; and
* + we know the key we want to insert into the parent
* (it's the "high key" on the left child page).
*
* We're ready to do the parent insertion. We need to hold onto the
* locks for the child pages until we locate the parent, but we can
* release them before doing the actual insertion (see Lehman and Yao
* for the reasoning).
*----------
*/
// 在父节点插入新节点B链接和新A的high key
_bt_insert_parent(rel, buf, rbuf, stack, is_root, is_only);
else
/* Do the update. No ereport(ERROR) until changes are logged */
START_CRIT_SECTION();
if (!_bt_pgaddtup(page, itemsz, itup, newitemoff))
elog(PANIC, "failed to add new item to block %u in index \"%s\"",
itup_blkno, RelationGetRelationName(rel));
MarkBufferDirty(buf);
delete
We consider deleting an entire page from the btree only when it’s become
completely empty of items. (Merging partly-full pages would allow better
space reuse, but it seems impractical to move existing data items left or
right to make this happen — a scan moving in the opposite direction
might miss the items if so.) Also, we never delete the rightmost page
on a tree level (this restriction simplifies the traversal algorithms, as
explained below). Page deletion always begins from an empty leaf page. An
internal page can only be deleted as part of a branch leading to a leaf
page, where each internal page has only one child and that child is also to
be deleted.
删除与查找类似,在找到要删除数据后,在leaf 中删除那条数据,不删除internal node上数据
参考
- http://db.cs.berkeley.edu/jmh/cs262b/treeCCR.html
- Efficient Locking for Concurrent Operations on B-Trees
- https://blog.csdn.net/popvip44/article/details/57468202
- A Symmetric Concurrent B-Tree Algorithm