BP神经网络用于波士顿房屋数据集上预测
一、BP神经网络的matlab工具箱
1.1、 BP神经网络创建函数
自R2010b版本以后,matlab神经网络工具箱对BP网络的创建函数进行了更新,更新后的函数如下:
net = feedforwardnet(hiddenSizes,trainFcn)
参数说明:
hiddenSizes:为一个行向量,表征一个或多个隐藏层所包含的神经元个数(默认为10,即仅有一个包含10个神经元的隐含层);
trainFcn:网络训练函数(默认为trainlm);
net:创建的网络。
1.2、BP神经网络训练函数
[net,tr] = train(net,P,T,Pi,Ai,EW)
参数说明:
net:训练前及训练后的网络;
P:为网络的输出向量;
T:为网络的输出向量;
Pi:初始的输入层延迟条件(默认为0);
Ai:初始的输出层延迟条件(默认为0);
EW:通过设置该参数可调整输出目标向量中各个元素的重要程度;
Tr:训练记录(包括步数和性能)。
注意:P和T的列数一定要相等。假设P为n1xm的矩阵,则m表示样本的个数,n1表示每个样本的特征维数。相应的T为n2xm的矩阵,n2为输出向量的维数,m同样表示样本的个数。
1.3、BP网络预测函数
函数sim用于利用训练好的BP网络进行仿真预测,其调用格式为:
[Y,Pf,Af,E,perf] = sim(net,P,Pi,Ai,T)
参数说明:
net:训练好的网络;
P:网络的输出向量;
Pi:初始的输入层延迟条件(默认为0);
Ai:初始的输出层延迟条件(默认为0);
T:网络目标向量(默认为0);
Y:网络输出向量;
Pf:最终的输出层延迟条件;
Af:最终的隐含层延迟条件;
E:网络误差向量;
perf:网络的性能
二、BP神经网络实例
2.1、利用神经网络进行数据分析一般步骤如下:
(1)、产生训练集和测试集
(2)、数据归一化(可选操作)
输出属性的取值不同属于同一个数量级,输入变量差异较大,因此在建立模型之前,先对数据进行归一化处理。
然而,需要说明的是,归一化并非一个不可或缺的处理步骤,针对具体问题应进行具体分析,从而决定是否进行归一化;
(3)、创建和训练模型
调用feedforwardnet()函数和train()函数。
(4)、仿真测试
调用sim函数。
(5)、反归一化(可选操作)
如果进行了步骤2,则需要对仿真测试结果数据按照之前归一化的规则进行反归一化操作,得到最后的真实数据
(6)、性能分析
2.2、使用波士顿房屋数据集进行神经网络测试
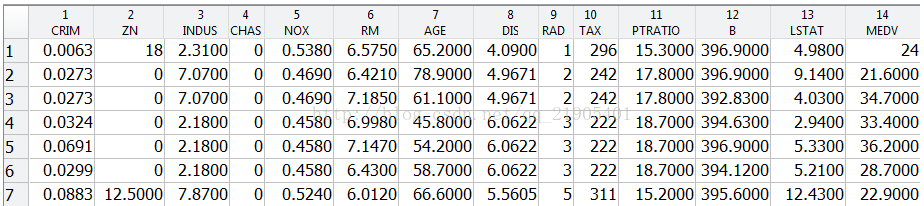
波士顿房屋数据集于1978年开始统计,共506个数据点,涵盖了麻省波士顿不同郊区房屋14种特征的信息。该数据集可以通过以下代码进行下载:
%%Download Housing Prices
filename = 'housing.txt';
urlwrite('http://archive.ics.uci.edu/ml/machine-learning-databases/housing/housing.data',filename);
inputNames = {'CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT'};
outputNames = {'MEDV'};
housingAttributes = [inputNames,outputNames];%%Import Data
formatSpec = '%8f%7f%8f%3f%8f%8f%7f%8f%4f%7f%7f%7f%7f%f%[^\n\r]';
fileID = fopen(filename,'r');
dataArray = textscan(fileID, formatSpec, 'Delimiter', '', 'WhiteSpace', '', 'ReturnOnError', false);
fclose(fileID);
housing = table(dataArray{1:end-1}, 'VariableNames', {'VarName1','VarName2','VarName3','VarName4','VarName5','VarName6','VarName7','VarName8','VarName9',...
'VarName10','VarName11','VarName12','VarName13','VarName14'});
%Delete the file and clear temporary variables
clearvars filename formatSpec fileID dataArray ans;
%%delete housing.txt
%%Read into a Table
housing.Properties.VariableNames = housingAttributes;
X = housing{:,inputNames};
y = housing{:,outputNames}; 具体的,各数据特征含义可参考下图:
2.3、实现代码
X为506x13矩阵(506为房屋数,13为特征维数),指特征向量;y为1x506矩阵,指对应的房价。使用13个房屋属性预测对应的房屋价值,即神经网络的输入向量为X',输出向量为Y'。根据2.1中的步骤,编写代码如下:
X = features;Y = prices;len = length(prices);
index = randperm(len);%生成1~len 的随机数
%%产生训练集和数据集
%训练集——前70%
p_train = features(index(1:round(len*0.7)),:);%训练样本输入
t_train = prices(index(1:round(len*0.7)),:);%训练样本输出
%测试集——后30%
p_test = features(index(round(len*0.7)+1:end),:);%测试样本输入
t_test = prices(index(round(len*0.7)+1:end),:);%测试样本输出
%%数据归一化
%输入样本归一化
[pn_train,ps1] = mapminmax(p_train');
pn_test = mapminmax('apply',p_test',ps1);
%输出样本归一化
[tn_train,ps2] = mapminmax(t_train');
%tn_test = mapminmax('apply',t_test',ps2);
%%神经网络
%创建和训练
net = feedforwardnet(5,'trainlm');%创建网络
net.trainParam.epochs = 5000;%设置训练次数
net.trainParam.goal=0.0000001;%设置收敛误差
[net,tr]=train(net,pn_train,tn_train);%训练网络
%网络仿真
b=sim(net,pn_test);%放入到网络输出数据
%%结果反归一化
predict_prices = mapminmax('reverse',b,ps2);
%%结果分析
t_test = t_test';
err_prices = t_test-predict_prices;
[mean(err_prices) std(err_prices)]
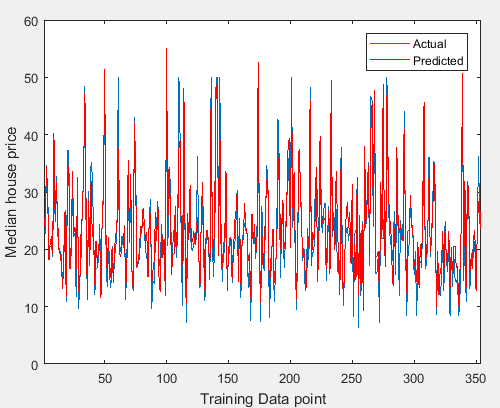
figure(1);
plot(t_test);
hold on;
plot(predict_prices,'r');
xlim([1 length(t_test)]);
hold off;
legend({'Actual','Predicted'})
xlabel('Training Data point');
ylabel('Median house price');