SVM入门实例可运行python代码完整版(简单可视化)

运行环境 anaconda 

python 版本 2.7.13

包含详细数据集和数据的使用，可视化结果，很快入门，代码如下

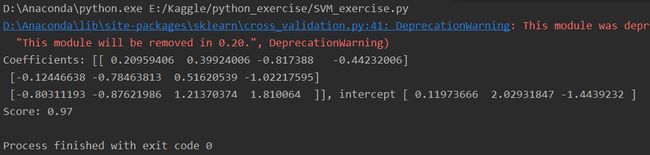
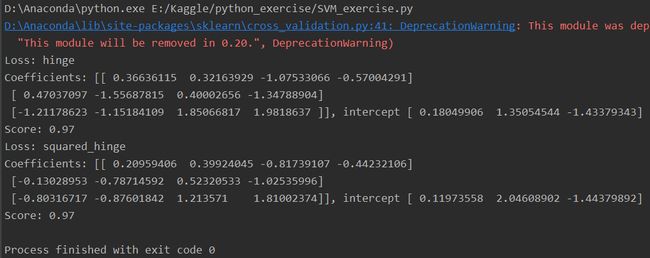
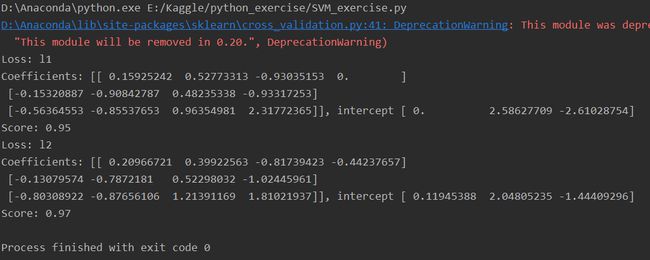
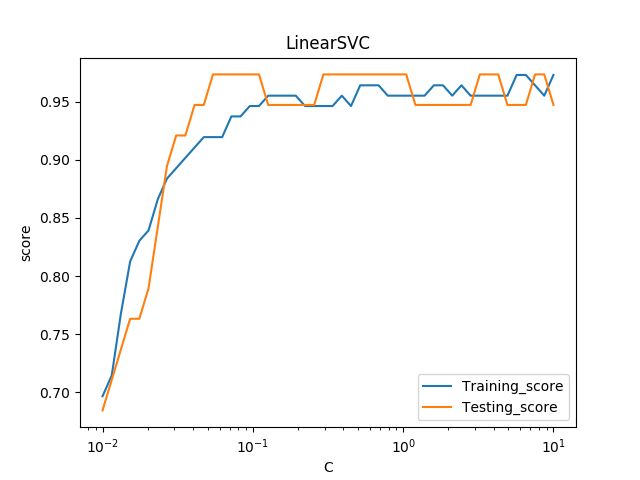
# -*- coding: utf-8 -*-
__author__ = 'LinearSVC线性分类支持向量机：包含惩罚项的'

# 导包
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, cross_validation, svm


# 数据集：鸢尾花数据集
'''
数据数 150
数据类别 3 (setosa, versicolor, virginica)
每个数据包含4个属性：sepal萼片长度、萼片宽度、petal花瓣长度、花瓣宽度
'''
def load_data_classfication():
    iris = datasets.load_iris()
    X_train = iris.data
    y_train = iris.target
    return cross_validation.train_test_split(X_train, y_train, test_size=0.25, random_state=0, stratify=y_train)


# 求得分类函数参数w, b
# 得出预测准确度
'''
调用默认线性分类函数，默认参数定义如下：
penalty = 'l2' 惩罚项
loss = 'squared_hinge' 合页损失函数的平方
dual = True 解决对偶问题
tol = 0.0001 终止迭代的阈值
C = 1.0 惩罚参数
multi_class = 'ovr' 多分类问题的策略：采用 one-vs-rest策略
fit_intercept = True 计算截距，即决策函数中的常数项
intercept-scaling = 1 实例X变成向量[X, intercept-scaling]，此时相当于添加了一个人工特征，该特征对所有实例都是常数值。
class-weight = None 认为类权重是1
verbose = 0 表示不开启verbose输出
random_state = None 使用默认的随机数生成器
max_iter = 1000 指定最大的迭代次数
'''

def test_LinearSVC(*data):
    X_train, X_test, y_train, y_test = data
    cls = svm.LinearSVC()
    cls.fit(X_train, y_train)
    print('Coefficients: %s, intercept %s' % (cls.coef_, cls.intercept_))
    print('Score: %.2f' % cls.score(X_test, y_test))

# 考察损失函数的影响
def test_LinearSVC_loss(*data):
    X_train, X_test, y_train, y_test = data
    losses = ['hinge', 'squared_hinge']
    for loss in losses:
        cls = svm.LinearSVC(loss=loss)
        cls.fit(X_train, y_train)
        print('Loss: %s' % loss)
        print('Coefficients: %s, intercept %s' % (cls.coef_, cls.intercept_))
        print('Score: %.2f' % cls.score(X_test, y_test))

# 考察惩罚项参数影响 dual=True, penalty='l2'不支持
def test_LinearSVC_L12(*data):
    X_train, X_test, y_train, y_test = data
    L12 = ['l1', 'l2']
    for p in L12:
        cls = svm.LinearSVC(penalty=p, dual=False)
        cls.fit(X_train, y_train)
        print('Loss: %s' % p)
        print('Coefficients: %s, intercept %s' % (cls.coef_, cls.intercept_))
        print('Score: %.2f' % cls.score(X_test, y_test))

# 考察惩罚项
def test_LinearSVC_C(*data):
    X_train, X_test, y_train, y_test = data
    Cs = np.logspace(-2, 1)
    train_scores = []
    test_scores = []
    for C in Cs:
        cls = svm.LinearSVC(C=C)
        cls.fit(X_train, y_train)
        train_scores.append(cls.score(X_train, y_train))
        test_scores.append(cls.score(X_test, y_test))

    # 绘图
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.plot(Cs, train_scores, label='Training_score')
    ax.plot(Cs, test_scores, label='Testing_score')
    ax.set_xlabel(r'C')
    ax.set_ylabel(r'score')
    ax.set_xscale('log')
    ax.set_title('LinearSVC')
    ax.legend(loc='best')
    #plt.show()
    plt.savefig('C_LinearSVC.png')
# 调用test_LinearSVC函数
if __name__ == '__main__':

    X_train, X_test, y_train, y_test = load_data_classfication() #结果1
    #test_LinearSVC(X_train, X_test, y_train, y_test) #结果2
    #test_LinearSVC_loss(X_train, X_test, y_train, y_test)  #结果3
    #test_LinearSVC_L12(X_train, X_test, y_train, y_test) #结果4
    test_LinearSVC_C(X_train, X_test, y_train, y_test) #结果5
'''结果1
Coefficients: [[ 0.20959406  0.39924006 -0.817388   -0.44232006]
 [-0.12446638 -0.78463813  0.51620539 -1.02217595]
 [-0.80311193 -0.87621986  1.21370374  1.810064  ]], intercept [ 0.11973666  2.02931847 -1.4439232 ]
Score: 0.97
'''

# 结果2

# 结果3

# 结果4

# 结果5