coursera 机器学习第六周

本周的内容主要分为两部分，第一部分：主要内容是偏差、方差以及学习曲线相关的诊断方法，为改善机器学习算法的决策提供依据；第二部分：主要内容是机器学习算法的错误分析以及数值评估标准：准确率（交叉验证集的误差）、查准率（precision）、查全率（recall）以及F值，还有大数据对机器学习的作用，并给出了机器学习算法的设计流程。

第一部分  

        （一）模型选择

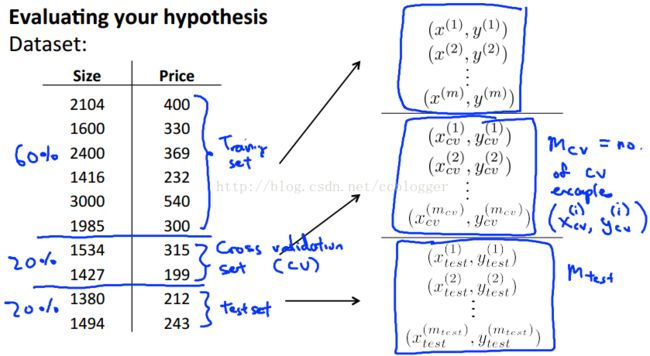
        在评估假设函数时，我们通常把数据集分成三部分：60%training set, 20%cross validation set, 20%test set. 分别用于拟合函数，模型选择和预测。

三个集合的误差如下所示（注意是没有正则化参数的）：

基于上面的划分，我们对模型选择的步骤为：

1、用测试集training set对多个模型（例如一次函数、二次函数、三次函数）进行训练；

2、用交叉验证集cross validation set验证上一步得到的多个假设函数，选择交叉验证集误差最小的模型；

3、用测试集test set对上一步选择的最优模型进行预测。

        下面是模型选择的过程：

以上问题其实是指关系到模型选择的中的一点——多项式的次数d。实际上我们还会去考虑这样两个参数：正则化参数λ、样本量m。而这些知识点涉及到我们下面要说的偏差（bias）、方差（variance）。

        （二）偏差（bias）、方差（variance）、学习曲线（learning curve）

根据上图我们可以发现以下对应关系：

欠拟合（underfit）	高偏差（high bias）
正常拟合（just right）	偏差和方差均较小
过拟合（overfit）	高方差（high variance）

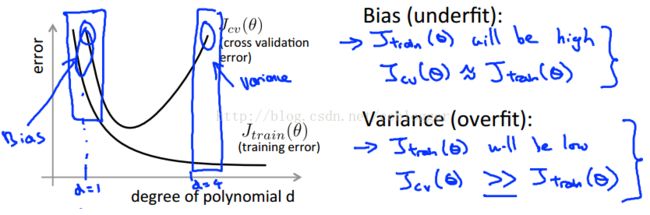
下面介绍特征量的度d、正则化参数λ、数据量m以及学习曲线：

1、特征量的度d

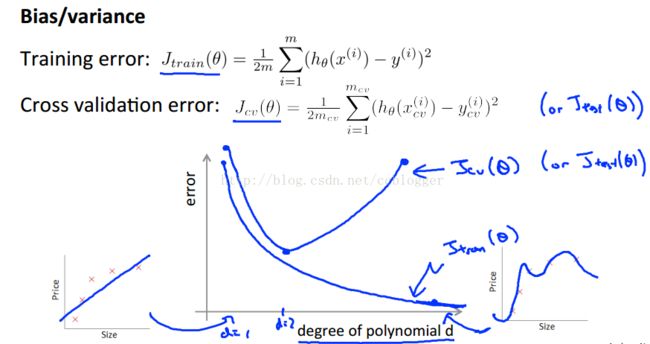
        例如上面线性回归的例子，当我们用二次函数拟合时，训练集和交叉验证集的误差都很小。但是当使用直线拟合时，不管使用多高级的算法去减小代价函数，偏差依然很大，这时候即：多项式次数d太小，导致高偏差、欠拟合；类似的当我们使用10次曲线去拟合，每个样本点都可以经过，训练集的误差近乎为0，但是当我们使用交叉验证集时会发现效果很差，误差很大，这时候即：多项式次数d太大，导致高方差、过拟合。

        多项式次数d与训练集、交叉验证集误差时间的关系为：

2、正则化参数λ

        正则化参数在第三周的学习中提到过，即λ越大，对θ惩罚越大：θ->0，假设函数是一条水平线，即欠拟合、高偏差；正则化参数越小，相当于正则化作用越弱，即过拟合、高方差。关系如下图所示：

3、样本量m和学习曲线learning curve

       学习曲线是误差与训练集和交叉验证集之间的关系，分为高偏差和高方差两种情况（欠拟合和过拟合）

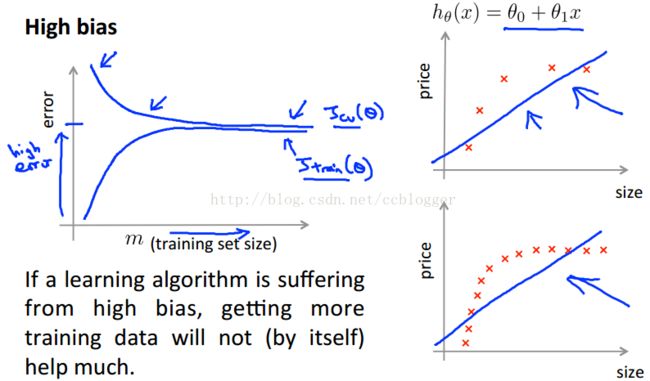
①高偏差（欠拟合）

从上图可以看出，高偏差情况下数据量的增加对误差的减小并没有效果，即m的增加对于算法的改进无益。

②高方差（过拟合）

从上图可以看出，通过增加样本量训练集的拟合程度很好，而且误差逐渐降低，说明m的增加对算法的改进有一定的帮助。

        （三）如何决策

        综上所诉，发现以下结论：

        ①训练集误差大、交叉验证集误差也大：欠拟合、高偏差、多项式次数d太小、λ太大；

        ②训练集误差小、交叉验证集误差却很大：过拟合、高方差、多项式次数d太大、λ太下、样本量太少。

这就为我们改善机器学习算法提供了依据：

    一般来说，使用一个大型的神经网络并使用正则化来修正过拟合通常比使用一个小型神经网络效果更好。但容易出现的问题是计算量会比较大。

第二部分

    （一）机器学习系统的设计流程

    1、刚开始使用简单算法尽快实现，然后再交叉验证集上实现并测试；

    2、画出学习曲线（learning curve）来决定是否需要更多的数据、更多的特征；

    3、误差分析（error analysis）：检查交叉验证集中被错误分类的样本，观察得到特性（例如垃圾邮件分类器例子中：什么类型的邮件容易被错误分类）。注意：误差分析（error analysis）不能决定是否对提高准确率有帮助。

    以垃圾邮件分类器为例，首先应该快速实现，即使你找不到太多的特征量，然后使用交叉验证集去检验，人工检查出错邮件的共同特征，通过这些特征和学习曲线来确定需要增加哪些特征量以及是否需要更多的数据量。

    （二）数值评估机器学习算法的标准

1、交叉验证集误差（cross validation error）

    设计的拟合函数交叉验证集误差很大，那么肯定不是一个很好的学习算法，但误差很小也不能证明该算法是一个很好的学习算法，下面介绍一个特殊的类：偏斜类（skewed classes）。

    例如某癌症的患病率是0.5%，设计的一个学习算法（综合考虑各种特征量最小化代价函数）得到交叉验证集准确率为99%，但是当你设计一种算法，所有预测结果都为0，此时的交叉验证集准确率为99.5%，显然这种预测并不是好的，这种就叫做偏斜类。

 

所以引入了查准率（precision）和查全率（recall）。

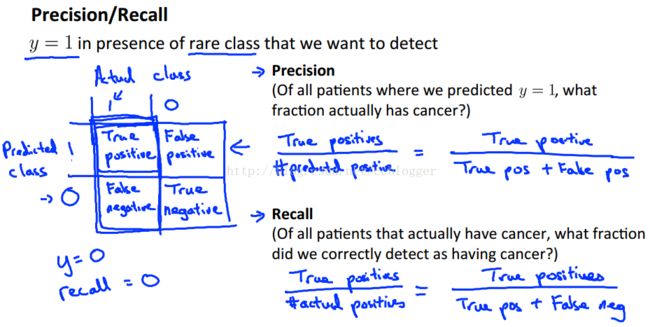
2、查准率（precision）、查全率（recall）与F值

查准率：你预测样本发病样本最后真发病的概率；

查全率：一个最终患病的样本，你之前也预测他患病的概率；

高的查准率意味着，我们在极为确定样本患病的情况下才告诉他患病(或者理解为不轻易预测他患病)；

高的查全率意味着，样本有可能患病我们就告诉他(或者理解为普世关怀)；

表达式如下图所示：

        例如前面预测癌症的例子，如果使所有的预测结果都为0，此时的准确率为99.5%，但是查全率为0，我们希望得到的学习算法是不仅要有高的预测准确率，还要有尽可能高的查准率和查全率，所以这种预测所有结果都为0的方法并不好。

        但是查准率和查全率往往不可兼得，所以需要权衡二者——F值。

        F值给出了一个很好判断查准率和查全率的数值计算标准（评估度量值），具体计算公式如下图：

    （三）机器学习的数据量

        大量数据往往能大幅度提高学习算法的最终性能，而不在于你是否使用更高级的求解算法。

当然要基于两点前提假设：

1.假设样本的特征能够提供充足的信息进行预测；

你不可能指望只知道房子的面积来预测房价，不管你是不是房地产方面的专家；

2.假设样本能提供尽可能多的特征量；

特征量越多，越不容易出现欠拟合、高偏差的问题；

所以也有这样的结论成立：

1.数据量越大，高方差、过拟合问题越不可能发生；

2.特征量越多，高偏差、欠拟合问题越不可能发生。