Coursera吴恩达机器学习课程 总结笔记及作业代码——第6周有关机器学习的小建议
1.1 Deciding what to try next
当你调试你的学习算法时,当面对测试集你的算法效果不佳时,你会怎么做呢?

- 获得更多的训练样本?
- 尝试更少的特征?
- 尝试获取附加的特征?
- 尝试增加多项式的特征?
- 尝试增加 λ ?
- 尝试减小 λ ?
由此我们引出了机器学习诊疗法
1.2 EvaluaDng a hypothesis

我们通过将数据集分成训练集和测试集,
将训练集训练出的参数用测试集数据测试性能。
线性回归时:
Jtest(θ)=12mtest∑mtesti=1(hθ(x(i)test)−y(i)test)2
逻辑回归时:
Jtest(θ)=−12mtest∑mtesti=1y(i)testlog(hθ(x(i)test))+(1−y(i)test)log(1−hθ(x(i)test))
1.3 Model selecDon and training/validaDon/test sets
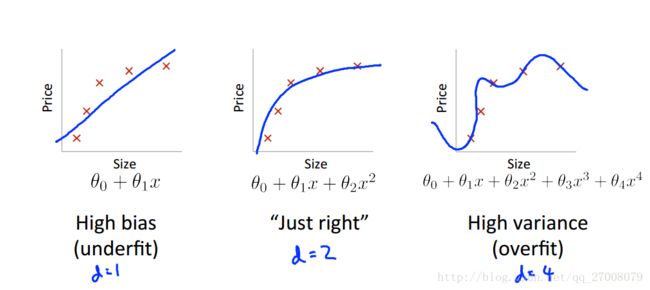
在多项式回归时,我们该怎么选择次数作为我们的假设模型呢?
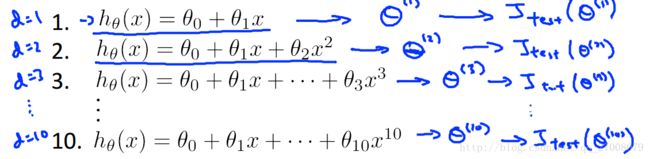
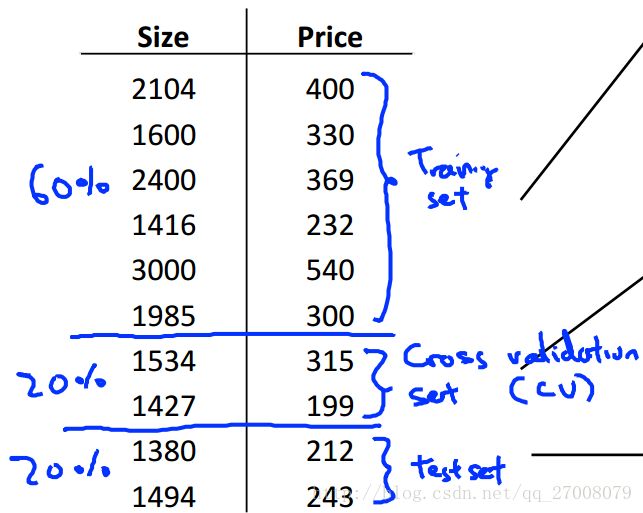
我们可以把数据集分为三类,训练集,交叉验证集和测试集,
用交叉验证集来作为评判选择的标准,选择合适的模型,而测试集则是作为算法性能的评判。
1.4 Diagnosing bias vs variance
Jtrain(θ)=12mtrain∑mtraini=1(hθ(x(i)train)−y(i)train)2
Jcv(θ)=12mcv∑mcvi=1(hθ(x(i)cv)−y(i)cv)2
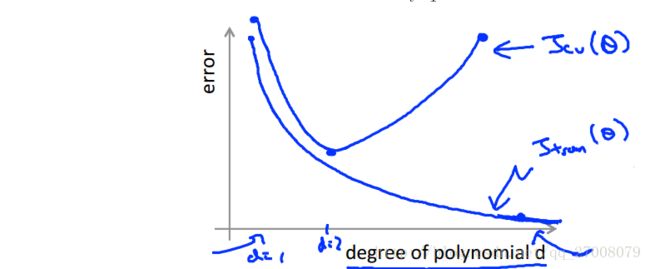
从图中可以看出,随着多项式次数的增大,训练集上的偏差逐渐变小,而交叉验证集上的偏差在减小到一定程度后开始升高。
在高偏差(欠拟合中)
Jtrain(θ) 很高
Jcv(θ)≈Jtrain(θ)
在高方差(过拟合中)
Jtrain(θ) 很低
Jcv(θ)≫Jtrain(θ)
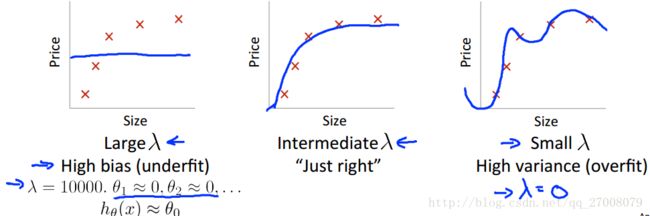
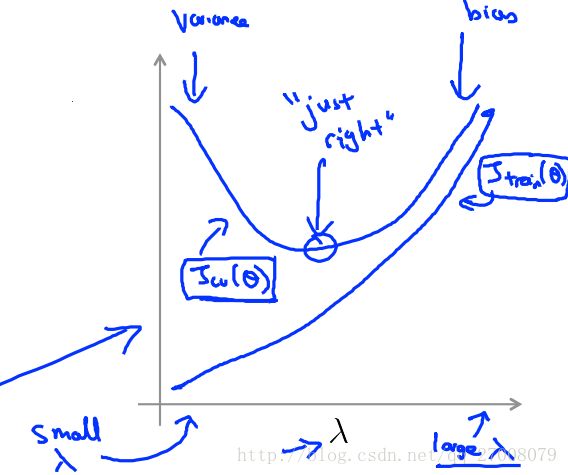
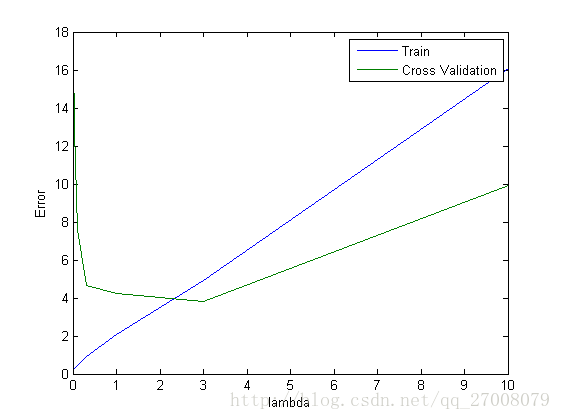
1.5 Regularization and bias/variance
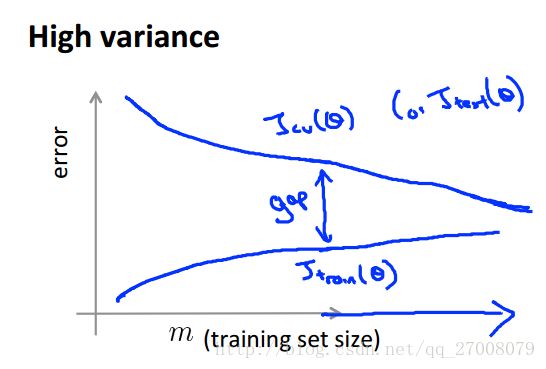
1.6 Learning curves
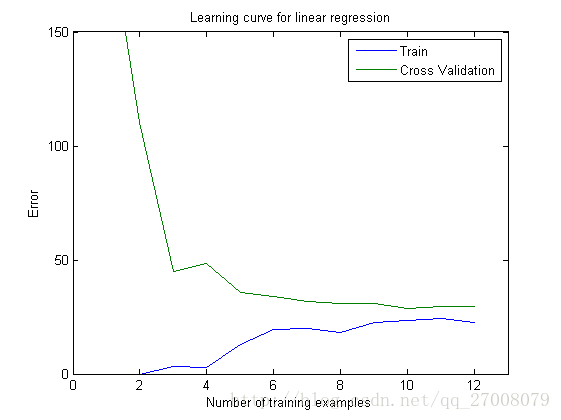
在高偏差的情况下,随着样本数目的增大,训练集上的误差和交叉验证集上的误差逐渐逼近。
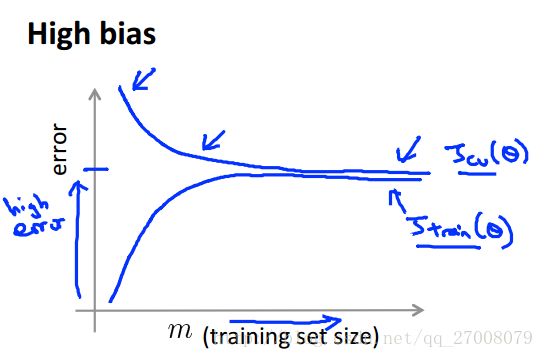
也就是说,增大样本的方法对高偏差的模型并不能起到一定作用
2.1 Machine learning system design
以做一个垃圾邮件分类器为例。
我们需要寻找最频繁出现出现的n个单词(10000~50000)作为训练集,而不是随意手工寻找100个单词。
下面的做法帮助你改善你的模型。
- 收集大量的数据。 eg. “honeypot”项目。
- 从邮件信息中找寻复杂的特征(例如从邮件首部)。
- 从邮件体中找寻复杂的特征(discount 和discounts是否被对待一致,关于标点符号的特征)。
- 使用复杂的算法来检测邮件中的拼写错误。
对误差的分析
- 先开始一个简单算法使你能快速实现它,在你的交叉验证集上测试它。
- 画出学习曲线来判断是否更多的数据,更多的特征有助于改进算法。
- 误差分析,在交叉验证集上检测你的算法,发现错误在某种类样本上出现的趋势。
将误差转变为一个单一的数值非常重要,否则很难判断我们所设计的学习算法的表现。
在误差分析中我们应使用定量计算来评判算法的表现。

2.2 Error metrics for skewed classes
以判断癌症的分类器为例。
建立逻辑回归模型 hθ(x) ,y=1表示有癌症,y=0则没有。
假设你的算法在测试集上只有1%的错误,可实际上,测试集中只有0.5%的病人患有癌症,因此我们可以通过下面的方法来提高正确率。

从上面的例子我们可以知道正确率不足以表现一个算法的优劣(在某些正例或反例及其少的数据集中),因此我们引入了Precision/Recall。
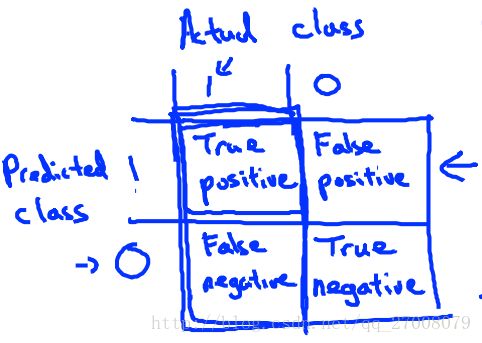
Precision(准确率)
在我们预测y=1的数据中,真正得癌症的比重。
True pospredicted pos=True posTrue pos+false pos
Recal(召回率)
在真正得癌症的数据中,我们预测癌症所占的比重。
True posactual pos=True posTrue pos+false neg
在前面我们提到,将误差转变为一个单一的数值非常重要,因为这样我们才能方便的比较不同算法之间的优劣。现在我们有precision和recall两个衡量标准,我们需要权衡两者。如果用Logistic回归模型预测病人是否患癌症,考虑下面的情况:
假设考虑到一个正常人如果误判为癌症,将会承受不必要的心理和生理压力,所以我们要有很大把握才预测一个病人患癌症(y=1)。那么一种方式就是提高阙值(threshold),不妨设我们将阙值提高到0.7,即:
Predict 1 if: hθ(x)≥0.7
Predict 0 if: hθ(x)<0.7
在这种情况下,我们将会有较高的precision,但是recall将会变低。
假设考虑到一个已经患癌症的病人如果误判为没有患癌症,那么病人可能将因不能及时治疗而失去宝贵生命,所以我们想要避免错过癌症患者的一种方式就是降低阙值,假设降低到0.3, 即
Predict 1 if: hθ(x)≥0.3
Predict 0 if: hθ(x)<0.3
在这种情况下,将得到较高的recall,但是precision将会下降。
为了将precision和Recal转变为一个单一数值,我们引入了 F=2PRP+R
3. 程序代码
在这次程序中,你首先进行了线性回归,然后画出了学习曲线,之后进行多项式回归,并画出学习曲线。最后比较了不同的 λ 在训练集和交叉验证集上的效果。
ex5.m
%% Machine Learning Online Class
% Exercise 5 | Regularized Linear Regression and Bias-Variance
%
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% exercise. You will need to complete the following functions:
%
% linearRegCostFunction.m
% learningCurve.m
% validationCurve.m
%
% For this exercise, you will not need to change any code in this file,
% or any other files other than those mentioned above.
%
%% Initialization
clear ; close all; clc
%% =========== Part 1: Loading and Visualizing Data =============
% We start the exercise by first loading and visualizing the dataset.
% The following code will load the dataset into your environment and plot
% the data.
%
% Load Training Data
fprintf('Loading and Visualizing Data ...\n')
% Load from ex5data1:
% You will have X, y, Xval, yval, Xtest, ytest in your environment
load ('ex5data1.mat');
% m = Number of examples
m = size(X, 1);
% Plot training data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 2: Regularized Linear Regression Cost =============
% You should now implement the cost function for regularized linear
% regression.
%
theta = [1 ; 1];
J = linearRegCostFunction([ones(m, 1) X], y, theta, 1);
fprintf(['Cost at theta = [1 ; 1]: %f '...
'\n(this value should be about 303.993192)\n'], J);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 3: Regularized Linear Regression Gradient =============
% You should now implement the gradient for regularized linear
% regression.
%
theta = [1 ; 1];
[J, grad] = linearRegCostFunction([ones(m, 1) X], y, theta, 1);
fprintf(['Gradient at theta = [1 ; 1]: [%f; %f] '...
'\n(this value should be about [-15.303016; 598.250744])\n'], ...
grad(1), grad(2));
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 4: Train Linear Regression =============
% Once you have implemented the cost and gradient correctly, the
% trainLinearReg function will use your cost function to train
% regularized linear regression.
%
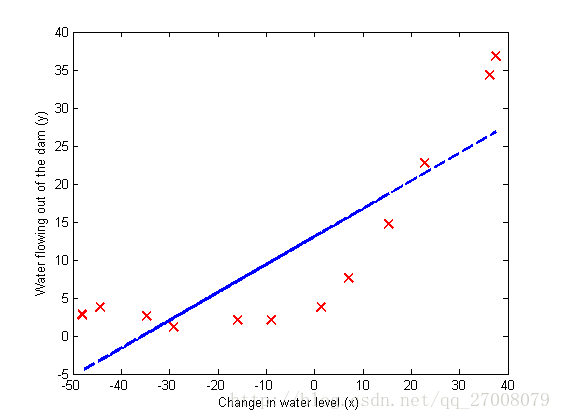
% Write Up Note: The data is non-linear, so this will not give a great
% fit.
%
% Train linear regression with lambda = 0
lambda = 0;
[theta] = trainLinearReg([ones(m, 1) X], y, lambda);
% Plot fit over the data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
hold on;
plot(X, [ones(m, 1) X]*theta, '--', 'LineWidth', 2)
hold off;
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 5: Learning Curve for Linear Regression =============
% Next, you should implement the learningCurve function.
%
% Write Up Note: Since the model is underfitting the data, we expect to
% see a graph with "high bias" -- Figure 3 in ex5.pdf
%
lambda = 0;
[error_train, error_val] = ...
learningCurve([ones(m, 1) X], y, ...
[ones(size(Xval, 1), 1) Xval], yval, ...
lambda);
plot(1:m, error_train, 1:m, error_val);
title('Learning curve for linear regression')
legend('Train', 'Cross Validation')
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 150])
fprintf('# Training Examples\tTrain Error\tCross Validation Error\n');
for i = 1:m
fprintf(' \t%d\t\t%f\t%f\n', i, error_train(i), error_val(i));
end
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 6: Feature Mapping for Polynomial Regression =============
% One solution to this is to use polynomial regression. You should now
% complete polyFeatures to map each example into its powers
%
p = 8;
% Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p);
[X_poly, mu, sigma] = featureNormalize(X_poly); % Normalize
X_poly = [ones(m, 1), X_poly]; % Add Ones
% Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test]; % Add Ones
% Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val]; % Add Ones
fprintf('Normalized Training Example 1:\n');
fprintf(' %f \n', X_poly(1, :));
fprintf('\nProgram paused. Press enter to continue.\n');
pause;
%% =========== Part 7: Learning Curve for Polynomial Regression =============
% Now, you will get to experiment with polynomial regression with multiple
% values of lambda. The code below runs polynomial regression with
% lambda = 0. You should try running the code with different values of
% lambda to see how the fit and learning curve change.
%
lambda = 0;
[theta] = trainLinearReg(X_poly, y, lambda);
% Plot training data and fit
figure(1);
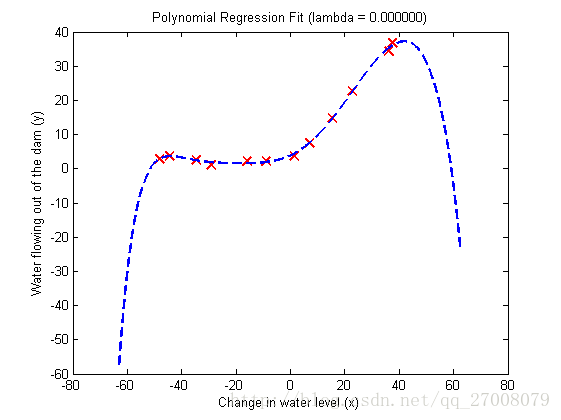
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
plotFit(min(X), max(X), mu, sigma, theta, p);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda));
figure(2);
[error_train, error_val] = ...
learningCurve(X_poly, y, X_poly_val, yval, lambda);
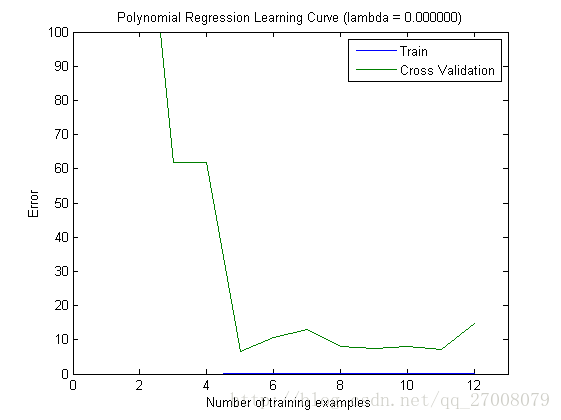
plot(1:m, error_train, 1:m, error_val);
title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 100])
legend('Train', 'Cross Validation')
fprintf('Polynomial Regression (lambda = %f)\n\n', lambda);
fprintf('# Training Examples\tTrain Error\tCross Validation Error\n');
for i = 1:m
fprintf(' \t%d\t\t%f\t%f\n', i, error_train(i), error_val(i));
end
fprintf('Program paused. Press enter to continue.\n');
pause;
%% =========== Part 8: Validation for Selecting Lambda =============
% You will now implement validationCurve to test various values of
% lambda on a validation set. You will then use this to select the
% "best" lambda value.
%
[lambda_vec, error_train, error_val] = ...
validationCurve(X_poly, y, X_poly_val, yval);
close all;
plot(lambda_vec, error_train, lambda_vec, error_val);
legend('Train', 'Cross Validation');
xlabel('lambda');
ylabel('Error');
fprintf('lambda\t\tTrain Error\tValidation Error\n');
for i = 1:length(lambda_vec)
fprintf(' %f\t%f\t%f\n', ...
lambda_vec(i), error_train(i), error_val(i));
end
fprintf('Program paused. Press enter to continue.\n');
pause;
linearRegCostFunction
function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
%LINEARREGCOSTFUNCTION Compute cost and gradient for regularized linear
%regression with multiple variables
% [J, grad] = LINEARREGCOSTFUNCTION(X, y, theta, lambda) computes the
% cost of using theta as the parameter for linear regression to fit the
% data points in X and y. Returns the cost in J and the gradient in grad
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
grad = zeros(size(theta));
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost and gradient of regularized linear
% regression for a particular choice of theta.
%
% You should set J to the cost and grad to the gradient.
%
J = 1/2/m* sum((X*theta - y) .^ 2) + lambda/2/m * sum(theta(2:end) .^ 2);
grad = 1/m* (X'*(X*theta - y));
grad(2:end) = grad(2:end) + lambda/m*theta(2:end);
% =========================================================================
grad = grad(:);
endlearningCurve.m
function [error_train, error_val] = ...
learningCurve(X, y, Xval, yval, lambda)
%LEARNINGCURVE Generates the train and cross validation set errors needed
%to plot a learning curve
% [error_train, error_val] = ...
% LEARNINGCURVE(X, y, Xval, yval, lambda) returns the train and
% cross validation set errors for a learning curve. In particular,
% it returns two vectors of the same length - error_train and
% error_val. Then, error_train(i) contains the training error for
% i examples (and similarly for error_val(i)).
%
% In this function, you will compute the train and test errors for
% dataset sizes from 1 up to m. In practice, when working with larger
% datasets, you might want to do this in larger intervals.
%
% Number of training examples
m = size(X, 1);
% You need to return these values correctly
error_train = zeros(m, 1);
error_val = zeros(m, 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the cross validation errors in error_val.
% i.e., error_train(i) and
% error_val(i) should give you the errors
% obtained after training on i examples.
%
% Note: You should evaluate the training error on the first i training
% examples (i.e., X(1:i, :) and y(1:i)).
%
% For the cross-validation error, you should instead evaluate on
% the _entire_ cross validation set (Xval and yval).
%
% Note: If you are using your cost function (linearRegCostFunction)
% to compute the training and cross validation error, you should
% call the function with the lambda argument set to 0.
% Do note that you will still need to use lambda when running
% the training to obtain the theta parameters.
%
% Hint: You can loop over the examples with the following:
%
% for i = 1:m
% % Compute train/cross validation errors using training examples
% % X(1:i, :) and y(1:i), storing the result in
% % error_train(i) and error_val(i)
% ....
%
% end
%
% ---------------------- Sample Solution ----------------------
for i=1:m
theta = trainLinearReg(X(1:i, :), y(1:i), lambda);
error_train(i) = linearRegCostFunction(X(1:i, :), y(1:i), theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end
% -------------------------------------------------------------
% =========================================================================
endvalidationCurve.m
function [lambda_vec, error_train, error_val] = ...
validationCurve(X, y, Xval, yval)
%VALIDATIONCURVE Generate the train and validation errors needed to
%plot a validation curve that we can use to select lambda
% [lambda_vec, error_train, error_val] = ...
% VALIDATIONCURVE(X, y, Xval, yval) returns the train
% and validation errors (in error_train, error_val)
% for different values of lambda. You are given the training set (X,
% y) and validation set (Xval, yval).
%
% Selected values of lambda (you should not change this)
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
% You need to return these variables correctly.
error_train = zeros(length(lambda_vec), 1);
error_val = zeros(length(lambda_vec), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Fill in this function to return training errors in
% error_train and the validation errors in error_val. The
% vector lambda_vec contains the different lambda parameters
% to use for each calculation of the errors, i.e,
% error_train(i), and error_val(i) should give
% you the errors obtained after training with
% lambda = lambda_vec(i)
%
% Note: You can loop over lambda_vec with the following:
%
% for i = 1:length(lambda_vec)
% lambda = lambda_vec(i);
% % Compute train / val errors when training linear
% % regression with regularization parameter lambda
% % You should store the result in error_train(i)
% % and error_val(i)
% ....
%
% end
%
%
for i=1:size(lambda_vec, 1)
theta = trainLinearReg(X, y, lambda_vec(i));
error_train(i) = linearRegCostFunction(X, y, theta, 0);
error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end
% =========================================================================
end