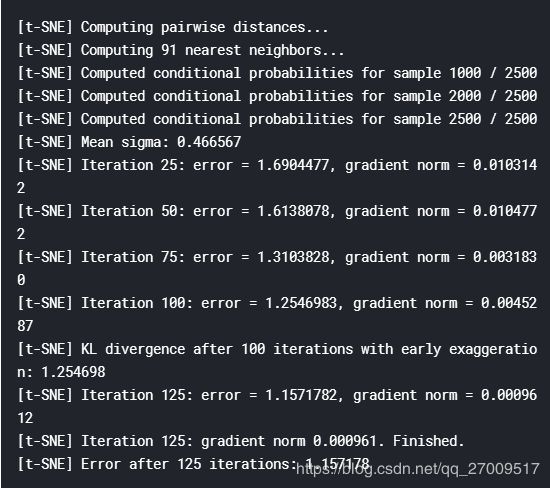
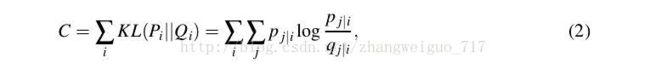TSNE
1.流形学习的概念
流形学习方法(Manifold Learning),简称流形学习,自2000年在著名的科学杂志《Science》被首次提出以来,已成为信息科学领域的研究热点。在理论和应用上,流形学习方法都具有重要的研究意义。
假设数据是均匀采样于一个高维欧氏空间中的低维流形,流形学习就是从高维采样数据中恢复低维流形结构,即找到高维空间中的低维流形,并求出相应的嵌入映射,以实现维数约简或者数据可视化。它是从观测到的现象中去寻找事物的本质,找到产生数据的内在规律。
简单地理解,流形学习方法可以用来对高维数据降维,如果将维度降到2维或3维,我们就能将原始数据可视化,从而对数据的分布有直观的了解,发现一些可能存在的规律。
官方代码思想是一遍聚类一遍降维,其实也是一种比较好的自动聚类方法。
高维数据每个数据点被认为是一种正太分布数据(正太有三好),低维数据同样,然后让高维数据和低维数据相似度最大。又因为t分布好算而且和正太分布逼近,所以用了t分布来算就成了tsne方法。
2.流形学习的分类
可以将流形学习方法分为线性的和非线性的两种,线性的流形学习方法如我们熟知的主成份分析(PCA),非线性的流形学习方法如等距映射(Isomap)、拉普拉斯特征映射(Laplacian eigenmaps,LE)、局部线性嵌入(Locally-linear embedding,LLE)。
当然,流形学习方法不止这些,因学识尚浅,在此我就不展开了,对于它们的原理,也不是一篇文章就能说明白的。对各种流形学习方法的介绍,网上有一篇不错的读物(原作已找不到):
3.高维数据降维与可视化
对于数据降维,有一张图片总结得很好 :
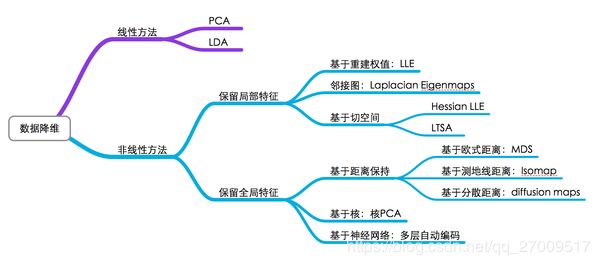
图中基本上包括了大多数流形学习方法,不过这里面没有t-SNE,相比于其他算法,t-SNE算是比较新的一种方法,也是效果比较好的一种方法。t-SNE是深度学习大牛Hinton和lvdmaaten(他的弟子?)在2008年提出的,lvdmaaten对t-SNE有个主页介绍:tsne,包括论文以及各种编程语言的实现。
接下来是一个小实验,对MNIST数据集降维和可视化,采用了十多种算法,算法在sklearn里都已集成,画图工具采用matplotlib。大部分实验内容都是参考sklearn这里的example,稍微做了些修改
- 加载数据
选用kaggle的Quora Question Pairs的比赛的数据,注册就可下载。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from subprocess import check_output
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.tools as tls
df = pd.read_csv("/train.csv").fillna("")
df.head()
-数值化
dfq1, dfq2 = dfs[['qid1', 'question1']], dfs[['qid2', 'question2']]
dfq1.columns = ['qid1', 'question']
dfq2.columns = ['qid2', 'question']
# merge two two dfs, there are two nans for question
dfqa = pd.concat((dfq1, dfq2), axis=0).fillna("")
nrows_for_q1 = dfqa.shape[0]/2
dfqa.shape
# Transform questions by TF-IDF.
from sklearn.feature_extraction.text import TfidfVectorizer, HashingVectorizer
mq1 = TfidfVectorizer(max_features = 256).fit_transform(dfqa['question'].values)
diff_encodings = np.abs(mq1[::2] - mq1[1::2])
diff_encodings
- 使用
from sklearn.manifold import TSNE
tsne = TSNE(
n_components=3,
init='random', # pca
random_state=101,
method='barnes_hut',
n_iter=1000,
verbose=2,
angle=0.5
).fit_transform(diff_encodings.toarray())
trace1 = go.Scatter3d(
x=tsne[:,0],
y=tsne[:,1],
z=tsne[:,2],
mode='markers',
marker=dict(
sizemode='diameter',
color = dfs['is_duplicate'].values,
colorscale = 'Portland',
colorbar = dict(title = 'duplicate'),
line=dict(color='rgb(255, 255, 255)'),
opacity=0.75
)
)
data=[trace1]
layout=dict(height=800, width=800, title='test')
fig=dict(data=data, layout=layout)
py.iplot(fig, filename='3DBubble')

sklearn的教程
https://scikit-learn.org/stable/auto_examples/manifold/plot_lle_digits.html
SNE、TSNE
TSNE是由SNE衍生出的一种算法,SNE最早出现在2002年,它改变了MDS和ISOMAP中基于距离不变的思想,将高维映射到低维的同时,尽量保证相互之间的分布概率不变,SNE将高维和低维中的样本分布都看作高斯分布,而Tsne将低维中的坐标当做T分布,这样做的好处是为了让距离大的簇之间距离拉大,从而解决了拥挤问题。从SNE到TSNE之间,还有一个对称SNE,其对SNE有部分改进作用。
SNE算法
对称SNE算法
TSNE算法(***)
1、SNE
高维数据用X表示,Xi表示第i个样本,低维数据用Y表示,则高维中的分布概率矩阵P定义如下:
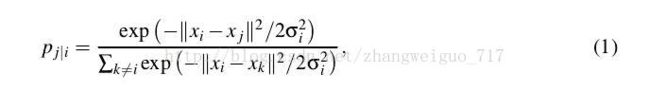
P(i,j)表示第i个样本分布在样本j周围的概率。delta是依据最大熵原理来决定,entropy=sum(pi*log(pi)),以每个样本点作为中心的delta都需要使得最后分布的熵较小,通常以log(k)为上限,k为你所决定的邻域点的个数。
低维中的分布概率矩阵计算如下:

这里我们把低维中的分布看作是均衡的,每个delta都是0.5,由此可以基本判断最后降维之后生成的分布也是一个相对均匀的分布。
随机给定一个初始化的Y,进行优化,使得Y的分布矩阵逼近X的分布矩阵。我们给定目的函数,用KL散度来定义两个不同分布之间的差距:

每次梯度下降的步长可设定固定或者自适应、随机等,也可以加上一个动量的梯度,初始值一般设为1e-4的随机正态分布。
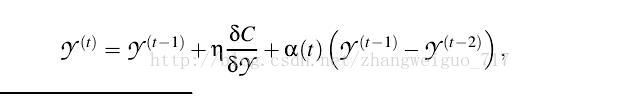
2、对称SNE
顾名思义,就是让高维和低维中的概率分布矩阵是对称的,能方便运算,但是对拥挤问题无改进。

同样采用KL散度作为两个分布之间的差异标准,只是梯度有一些改变:
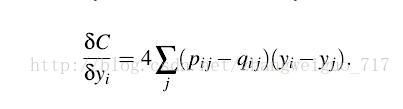
3、TSNE
TSNE对高维中的分布采用对称SNE中的做法,低维中的分布则采用更一般的T分布,也是对称的,我们可以发现sum§=sum(Q)=1。
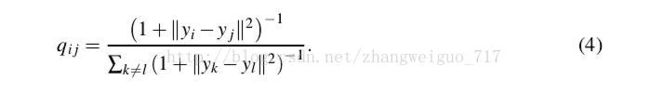
TSNE算法流程如下:

reference:
https://www.cnblogs.com/bonelee/p/7849867.html