【深度学习】线性回归（一）原理及python从0开始实现

线性回归

线性模型（linear model）通过属性的线性组合来进行预测，形如$y=wx+b$. 线性回归可以看成是单层的神经网络，包含了机器学习中模型的最基本的思想。
当定数据集$D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}，y_i\in R$，线性回归（linear regression）试图得到一个线性函数来预测实值输出，如下所示：
$$f(x)=w^{T}x+b$$
其中$w=(w_1,w_2,...w_d),x=(x_1,x_2,...,x_m)$, $x$是一个矩阵，$|x_i|=m$实际上就是预测对象的属性个数。 当$w$和$b$确定之后，线性模型就确定了。

单个属性的情况

一种最简单的场景就是需要预测的对象仅有一个属性来描述，上述数据集退化为：$D=\{(x_i,y_i){\}}_{i=1}^m$. 此时线性回归试图学习到一个函数：$$f(x_i)=w{x}_i+b,使得f(x_i)\approx y_i$$ 问题的关键在于如何确定$w$和$b$的值！

在回归任务中，通常使用均方误差（mean squared error）来衡量$f(x)$和$y$的差别，即我们通常所说的损失函数。我们需要得到当${\sum }_{i=1}^m(f(x_i)-y_i{)}^2$最小时，$w$和$b$的值，我们记为：$$(w^{\ast },b^{\ast })=ar{g}_{w,b}min\sum _{i=1}^m(f(x_i)-y_i{)}^2$$
很容易可以发现，均方误差在几何上对应的是欧式距离，具有非常良好的几何意义。

观察上述问题，可以很容易地联想到“利用直线拟合平面上若干点”的问题，由此，可以采用“最小二乘法（least square method）”，其试图得到一条直线使得所有的点到直线的欧式距离之和最小，这里称之为线性回归模型的最小二乘参数估计。

将$w$和$b$看成未知数，记$E_{w,b}={\sum }_{i=1}^m(f(x_i)-y_i{)}^2={\sum }_{i=1}^m(y_i-w{x}_i-b{)}^2$，解方程组：
$$\{\begin{array}{c}\frac{\partial E_{w,b}}{\partial w}=0\\ \\ \frac{\partial E_{w,b}}{\partial b}=0\end{array}$$
可得：
$$\{\begin{array}{c}w=\frac{{\sum }_{i=1}^m{y}_i(x_i-\overline{x})}{{\sum }_{i=1}^m{x}_i^2-\frac{1}{m}({\sum }_{i=1}^m{x}_i{)}^2}\\ \\ b=\frac{1}{m}{\sum }_{i=1}^m{y}_i-w{x}_i\end{array}$$
其中$\overline{x}=\frac{1}{m}{\sum }_{i=1}^m{x}_i$为$x$的均值。

多元线性回归

在实际应用中，对象通常具有很多属性，这就引出了一个更加一般的情况，即样本由$d$个属性描述，此时试图学到$$f(x_i)=w^T{x}_i+b，使得f(x_i)\approx y_i$$
称之为多元线性回归（multivariable linear regression）。
类似的，使用最小二乘法来对$w$和$b$进行估计。为了矩阵运算的方便：

• 将每个样本的标记（tag）记为向量形式：$y=(y_1,y_2,...,y_m)$
• 利用一个向量来表示$w$和$b$，记为：$a=(w,b)$，此时数据集$D$表示为一个$m\ast (d+1)$大小的矩阵$X$，$m$表示样本大小，$d$表示属性个数。
  $$X=\left(\begin{array}{ccccc}{x}_{11}& x_{12}& ...& x_{1d}& 1\\ x_{21}& x_{22}& ...& x_{2d}& 1\\ ...& ...& ...& ...& ...\\ x_{m1}& x_{m2}& ...& x_{md}& 1\end{array}\right)$$

类似于单个属性情况，此时我们需要找到$a^{\ast }$满足：
$$a^{\ast }=ar{g}_{a}min(y-Xa{)}^T(y-Xa)$$
记$E_a=(y-Xa{)}^T(y-Xa)$，解方程$\frac{\partial E_a}{\partial a}=2X^T(Xa-y)=0$可得$a$的最优解称之为最优闭式解（closed-form）。

当$X^{T}X$为满秩矩阵（full-rank matrix）或者正定矩阵（positive definite matrix）时，上述方程有唯一解：$$a^{\ast }=(X^{T}X{)}^{-1}{X}^{T}y$$

然而现实场景中往往不满足满秩或者正定条件，此时存在多个解。最终选择哪个最为最优模型取决于算法的归纳偏好，常见的做法是引入正则化项（regularization）。

广义线性模型

比如我们需要学习到的模型为：$lny=wX+b$，其形式上为一个线性模型，但其实为一个“线性+对数”关系，即这里对$y$（即tag）进行了对数变换。当然，还有其他类似变换。

记这种变换为函数: $g(x),g(x)$单调可微，称：$$y=g^{-1}(w^{T}x+b)$$
为广义线性模型（Generalized Linear Model），其中$g(x)$称之为联系函数（link function）。

实验数据集

介绍

采用加州大学欧文分校（UCI）公开的数据集进行实验，数据集包括9568个样本，每个样本包含5个数据：温度AT、压力V、湿度AP、压强RH、输出电力PE，前四个表示样本属性，PE表示样本的tag。换句话说，我们希望训练得到如下线性模型：
$$PE=w^T(AT,V,AP,RH)+b,其中w=(w_1,w_2,w_3,w_4)$$

下载的数据集包含5个sheets，每个sheets是原始数据打乱的结果，这里我们仅简单实用其中一个Sheets的数据，使用.CSV格式数据进行实验（原文是为了方便进行统计检验）。

相关链接

数据集介绍：
http://archive.ics.uci.edu/ml/datasets/Combined+Cycle+Power+Plant
数据集下载：
http://archive.ics.uci.edu/ml/machine-learning-databases/00294/

Python实现

环境

• 编码环境：Anaconda3 + PyCharm + MacOS（最好保持python版本一致，后面两个不重要）
• 使用Anaconda主要是其集成了常用的python包，很方便；当然已经安装了Python3也没关系，安装相关的包亦可
• 对于上述不满足满秩存在多个解的情况，使用梯度下降进行近似
• 梯度下降方法在机器学习模型中应用范围较广（比如神经网络），这里不再详细介绍
• 梯度下降的基本思想是通过一个学习率$\alpha$来逐步调整$a$参数，直到达到预定的精度或者达到预定迭代次数为止

编码

最小二乘法

这里仅使用numpy包实现，自己编写数据预处理代码、最小二乘法的矩阵实现、均方差的计算代码等。

# coding=utf-8
# author: BebDong
# date: 2018/11/27
# use only numpy to do linear regression in least square method


import numpy as np
from numpy import dot
from numpy.linalg import inv

# read files: 9568 samples, 9569 rows with first row representing the meaning of each column
data_list_matrix = np.loadtxt(open('./sheets/Sheet1.csv'), delimiter=",", skiprows=1)

# extract attributes and tags respectively
data_list_attribute = data_list_matrix[:, 0:4]
data_list_tag = data_list_matrix[:, 4:5]

# we simply split the dataset: top 75% rows as training data(7176) and the rest as testing data(2392)
X_train = data_list_attribute[:7176]
X_test = data_list_attribute[7176:]
y_train = data_list_tag[:7176]
y_test = data_list_tag[7176:]

# add a column to X_train filled with 1
X_train = np.c_[X_train, np.ones((7176, 1))]
X_test = np.c_[X_test, np.ones((2392, 1))]

# least square method: w = ((X'X)^-1)X'y
a = dot(dot(inv(dot(X_train.T, X_train)), X_train.T), y_train)

# prediction
y_prediction = dot(X_test, a)

# mean squared error(MSE) to evaluate
error = y_prediction - y_test
MSE = np.sum(pow(error, 2)) / 2392
print('MSE: ', MSE)

使用sklearn和pandas简化

使用sklearn和pandas预定义的函数进行数据集的分割、线性回归、均方差计算等，简化上述过程。sklearn包进行线性回归使用的也是最小二乘法。

# coding=utf-8
# author: BebDong
# date: 2018/11/28
# use scikit-learn and pandas to do linear regression


import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn import metrics

# use pandas to read files
data = pd.read_csv('./sheets/Sheet1.csv')

# extract attributes and tags of samples from data
X = data[['AT', 'V', 'AP', 'RH']]
y = data[['PE']]

# split the dataset into training set and testing set
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)

# use scikit-learn to do linear regression
linearRegression = LinearRegression()
linearRegression.fit(X_train, y_train)

# print the parameters of the model
print('intercept: ', linearRegression.intercept_)
print('coefficient: ', linearRegression.coef_)

# testing set regression
y_prediction = linearRegression.predict(X_test)

# model evaluation by mean squared error(MSE) or root mean squared error(RMSE)
MSE = metrics.mean_squared_error(y_test, y_prediction)
print('MSE: ', MSE)

梯度下降

梯度下降的基本思想就是通过误差反过来对参数进行调整。
当$\frac{\partial E_a}{\partial a}=2X^T(Xa-y)=0$无法直接得到解时，采用梯度下降法进行近似求解，即：
$$a_{i+1}=a_i-\alpha \frac{\partial E_a}{\partial a}=a_i-\alpha X^T(Xa-y)$$使用梯度下降法将引入两个参数：学习率$\alpha$（或步长）和迭代次数epochs，迭代次数指使用上式进行调整的次数。

代码实现如下图所示，数据预处理和计算MSE等与最小二乘法实现一致：

# gradient descent
a_gradient = np.array([1., 1., 1., 1., 1.]).reshape(5, 1)
alpha = 0.00000000025
epochs = 100000
for i in range(epochs):
    error = dot(X_train, a_gradient) - y_train
    error_each_item = dot(X_train.T, error)
    a_gradient = a_gradient - alpha * error_each_item

需要注意的是，$alpha$和epochs这两个参数需要多次调整，上述参数是我调整之后比较好的结果。在这个实验中，学习率($\alpha$)不能调得过大，因为数据没有经过归一化处理，学习率稍大就会出现不收敛的情况。

方法比较

测试代码

这里直接将上述两种方法暴力地定义为两个函数进行比较了，一种比较好的习惯是对公共代码进行单独封装，方便维护。
另外：

• 对实现的方法进行了可视化显示
• 增加了交叉验证的实验

# coding=utf-8
# author: BebDong
# date: 2018/11/28
# to packaged into functions and do evaluation on these methods


import numpy as np
from numpy import dot
from numpy.linalg import inv

import pandas as pd
from sklearn.model_selection import train_test_split, cross_val_predict
from sklearn.linear_model import LinearRegression
from sklearn import metrics

import matplotlib.pyplot as plt

import time


def visualMSE(y_test, y_prediction, title):

    # visualisation
    figure, ax = plt.subplots()
    ax.scatter(y_test, y_prediction)
    ax.plot([y_test.min(), y_test.max()], [y_test.min(), y_test.max()], 'k--', lw=4)
    ax.set_xlabel('measured')
    ax.set_ylabel('predicted')
    ax.set_title(title)
    plt.show()

    # MSE
    MSE = metrics.mean_squared_error(y_test, y_prediction)
    return MSE


def least_square():
    # read files: 9568 samples, 9569 rows with first row representing the meaning of each column
    data_list_matrix = np.loadtxt(open('./sheets/Sheet3.csv'), delimiter=",", skiprows=1)

    # extract attributes and tags respectively
    data_list_attribute = data_list_matrix[:, 0:4]
    data_list_tag = data_list_matrix[:, 4:5]

    # we simply split the dataset: top 75% rows as training data(7176) and the rest as testing data(2392)
    X_train = data_list_attribute[:7176]
    X_test = data_list_attribute[7176:]
    y_train = data_list_tag[:7176]
    y_test = data_list_tag[7176:]

    # add a column to X_train filled with 1
    X_train = np.c_[X_train, np.ones((7176, 1))]
    X_test = np.c_[X_test, np.ones((2392, 1))]

    # least square method: w = ((X'X)^-1)X'y
    a = dot(dot(inv(dot(X_train.T, X_train)), X_train.T), y_train)
    # prediction
    y_prediction = dot(X_test, a)
    MSE_least_square = visualMSE(y_test, y_prediction, 'least square without sklearn')
    print('MSE when least square: ', MSE_least_square)

    # gradient descent
    a_gradient = np.array([1., 1., 1., 1., 1.]).reshape(5, 1)
    alpha = 0.00000000025
    epochs = 100000
    for i in range(epochs):
        error = dot(X_train, a_gradient) - y_train
        error_each_item = dot(X_train.T, error)
        a_gradient = a_gradient - alpha * error_each_item
    # prediction
    y_prediction = dot(X_test, a_gradient)
    MSE_gradient = visualMSE(y_test, y_prediction, 'gradient descent')
    print('MSE when gradient descent: ', MSE_gradient)


def sklearn_way():
    # use pandas to read files
    data = pd.read_csv('./sheets/Sheet3.csv')

    # extract attributes and tags of samples from data
    X = data[['AT', 'V', 'AP', 'RH']]
    y = data[['PE']]

    # split the dataset into training set and testing set
    X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=1)
    # use scikit-learn to do linear regression
    linearRegression = LinearRegression()
    linearRegression.fit(X_train, y_train)
    # testing set regression
    y_prediction = linearRegression.predict(X_test)
    # MSE
    MSE = visualMSE(y_test, y_prediction, 'least square with sklearn')
    print('MSE when sklearn: ', MSE)

    # 10 cross validation
    prediction = cross_val_predict(linearRegression, X, y, cv=10)
    MSE_cross_vali = visualMSE(y, prediction, 'MSE when cross validation')
    print('MSE when cross validation: ', MSE_cross_vali)


def main():
    # begin
    start = time.perf_counter()
    # linear regression
    least_square()
    sklearn_way()
    # end
    end = time.perf_counter()
    print("time cost: ", end - start)


if __name__ == '__main__':
    main()

结果

下面的结果仅适用于当前实验数据和当前参数配置，不具有普适性，即不代表各种方法的普遍优劣性。

MSE分析

如下图所示，可以看到：

• 最小二乘法的结果优于梯度下降的方法
• 对于最小二乘法，使用sklearn包来实现相比于自己实现效果略好，因为使用sklearn包时将隐式对数据进行归一化处理
• 均使用skearn包时，交叉验证得到的结果比随机划分数据集得到的结果略差

可视化分析

如下为模型的可视化展示，图中横坐标为测量值，纵坐标为模型的预测值。图中的点越集中分布于黑色虚线（$y=x$）周围，表面预测值和实际值越接近，模型越好，




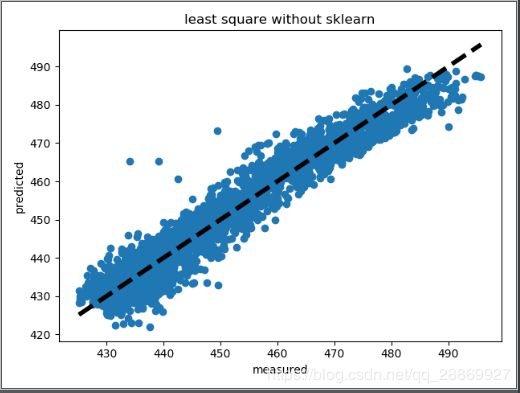
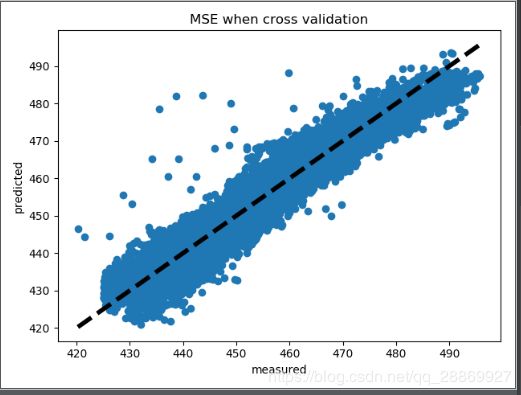
观察可视化图形，可以发现：

• 使用最小二乘法模型相比于梯度下降模型，绘制的点更加集中于直线$y=x$周围，表示本实验中最小二乘法的结果优于梯度下降；
• 这和利用MSE得出的实验结论是一致的。

数据归一化处理

零均值单位方差归一化

对于自己编程实现的最小二乘法和梯度下降法，使用的是numpy读取数据，这里直接使用sklearn提供的函数对数据集进行归一化处理（零均值单位方差）：

from sklearn import preprocessing
# read files: 9568 samples, 9569 rows with first row representing the meaning of each column
data_list_matrix = np.loadtxt(open('./sheets/Sheet3.csv'), delimiter=",", skiprows=1)
# data normalization
data_list_matrix = preprocessing.scale(data_list_matrix)

此时，梯度下降学习率需要进行相应调整，我使用的参数如下：

alpha = 0.000002
epochs = 2500

对于使用sklearn包实现的线性回归，使用pandas读取数据，使用Z-score对数据集进行归一化处理（零均值单位方差）：

# use pandas to read files
data = pd.read_csv('./sheets/Sheet3.csv')
# data normalization
data = (data - data.mean()) / data.std()

结果

MSE结果：对比归一化前后梯度下降法的参数及运行时间，可以发现对数据进行归一化以后，采用梯度下降法可以快速收敛。从MSE和可视化结果中可以看到，梯度下降的结果已经很接近利用最小二乘法直接得到的最优结果了。
有时候这种时间代价的差别可能是跨数量级的。

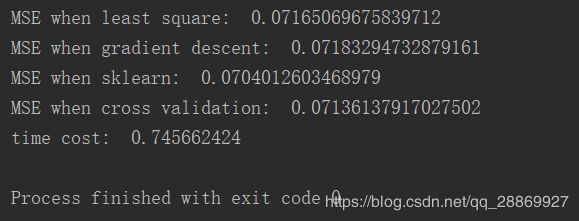
可视化结果：

完整源码

Github自取：
https://github.com/BebDong/LinearRegression.git

PS：对于梯度下降方法，可以对$(\alpha ,epoch)$ 两个参数进行多次调整，看看能否得到更优的结果呢？