Model-Based Value Expansion for Efficient Model-Free Reinforcement Learning
文献目录
作者通过一种很巧妙的方式把环境模型引入到Model-free RL算法中(包括了short horizon和TD-k技巧)。传统方法对于Q值的预估(比如DDPG/DQN)是通过bootstrapped的方式来更新参数的,在这篇文章中,作者把环境模型先rollout一定步数之后再进行Q值预估。也就是说,在传统的更新方式中,target Q值是使用的是下一步Q值的预估,而在这里,target Q值是先通过环境模型进行模拟一段路径之后,再进行Q值预估。这样Q值的预估就融合了基于环境模型的短期预估以及基于target_Q网络的长期预估。
文章目录
- 1. INTRODUCTION
- 3. Model-Based Value Expansion
- 3.1 Value Estimation Error
- 3.2 Deep Reinforcement Learning Implementation
- 4. Results
- 4.1 Performance
- 4.2 MVE as Critic Improvement
- 5. Related works
- References
1. INTRODUCTION
- 丰富的值函数近似器能够很好地完成复杂的任务,但需要与真实世界进行不切实际的大量交互;
- 在相当受限的环境下,基于模型(MB)的方法可以使用习得的模型快速达到近似最优的控制;
- 复杂的环境需要高容量的模型(如更深的神经网络),而这些模型又容易在那些最需要它们的低数据区中过度拟合;
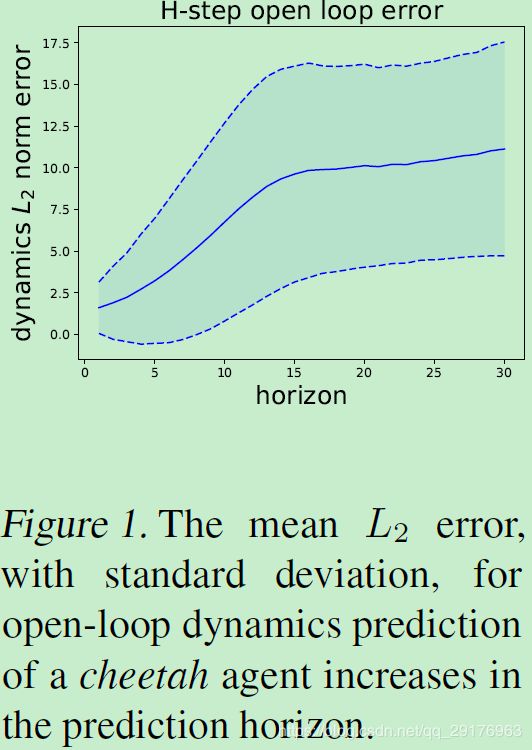
- 长期动态预测的难度进一步加剧了模型的不准确性(如图1)。
即MF方法可以取得很好的渐进性能,但样本复杂度高;而MB方法能够高效学习,但难以解决复杂问题。
我们提出了基于模型的价值扩张(model-based value expansion,MVE),这是一种混合算法,它使用动态模型来模拟短期horizon,用Q-learning方法估计仿真horizon以外的长期价值。 这通过为训练过程提供更高质量的目标值来改善Q-learning。 将价值估计拆分成短期MB模块和长期未来MF模块提供基于模型的价值估计,其(1)在价值估计和模型使用之间创建解耦的接口,以及(2)不需要可微动态。
本方案中,我们对模型的信任决定了horizon的选择,我们相信模型可以在horizon上做出准确的估计。这个horizon是一个可解释的度量,适用于许多动力学模型类。
通过将模型结合到Q-value目标估计中,我们仅要求模型能够进行前向预测。 与随机价值梯度(SVG)相比,我们对潜在动态没有做出可微分性假设,这通常包括非可微现象,如接触相互作用。 使用一个奖励密集环境的近似的、很少步骤的模拟,改进的值估计为actor-critic方法提供了足够的信号,以便更快地学习。
3. Model-Based Value Expansion
MVE通过假定我们有一个近似的动力学模型 f ^ : S × A → S \hat{f}:S\times A\rightarrow S f^:S×A→S和真实的reward function r r r来改进策略 π \pi π下的值估计。这种改进的价值估计可以用于训练批评家在回报密集的环境中更快地掌握任务。
我们假设模型对于深度 H H H是accurate的,即对于固定策略 π \pi π,当根据 f ^ π = f ^ π ( ⋅ , π ( ⋅ ) ) \hat{f}^\pi=\hat{f}^\pi(\cdot,\pi(\cdot)) f^π=f^π(⋅,π(⋅))和 π \pi π选择行为(actions)时,我们使用 f ^ \hat{f} f^来估计(想象)未来发生的状态转换。我们使用这些未来的转换来估计价值。
Definition 3.1 (H-Step Model Value Expansion):
使用由策略 π \pi π和模型 s ^ t = f ^ π ( s ^ t − 1 ) \hat{s}_t=\hat{f}^\pi(\hat{s}_{t-1}) s^t=f^π(s^t−1)获得的想象回报 r ^ t = r ( s ^ t , π ( s ^ t ) ) \hat{r}_t=r(\hat{s}_t,\pi(\hat{s}_t)) r^t=r(s^t,π(s^t)),我们为给定状态 V π ( s 0 ) V^\pi(s_0) Vπ(s0)的值定义H步模型值扩展(MVE)估计:
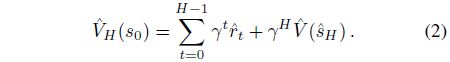
给定随机动力学的生成模型和策略,通过将方程2与蒙特卡罗方法相结合,这种方法可以扩展到随机策略和动力学。
由于 r ^ t \hat{r}_t r^t是从动作 a ^ t = π ( s ^ t ) \hat{a}_t=\pi(\hat{s}_t) a^t=π(s^t)中导出的,这是on-policy的,因此即使对于离散情况(确定性情况就算是off-policy也不需要),MVE也不需要重要性权重。
虽然MVE在H步视界不稀疏的情况下最有用,但即使在稀疏的奖励设置中,预测未来状态也将提高批评者的准确性。最后MVE也可以应用于行为价值函数的估计:
- 定义 a ^ 0 ≜ a 0 \hat{a}_0\triangleq a_0 a^0≜a0,
则对于 t > 0 t>0 t>0有 a ^ t = π ( s ^ t ) \hat{a}_t=\pi(\hat{s}_t) a^t=π(s^t); - 定义 V ^ ( s ^ H ) ≜ Q ^ ( s ^ H , a ^ H ) \hat{V}(\hat{s}_H)\triangleq\hat{Q}(\hat{s}_H,\hat{a}_H) V^(s^H)≜Q^(s^H,a^H),
可以利用状态-动作批评家 Q ^ \hat{Q} Q^来估计 Q ^ H ( s 0 , a 0 ) \hat{Q}_H(s_0,a_0) Q^H(s0,a0)。
3.1 Value Estimation Error
在本节中,我们将讨论MVE估计改善均方误差(MSE)的条件:
![]()
ν \nu ν为状态分布。我们强调,即使假设一个理想的模型,MB和MF的单纯组合也不能保证改进的估计。 此外,虽然我们的分析将在状态值估计上进行,但它可以自然地扩展到状态 - 动作 - 值估计。
回忆H-depth模型精度假设:如果我们观察到状态 s 0 s_0 s0,对于 t ≤ H t\le H t≤H,我们可以想象 s ^ t ≈ s t , a ^ t ≈ a t , r ^ t ≈ r t \hat{s}_t\approx s_t,\hat{a}_t\approx a_t,\hat{r}_t\approx r_t s^t≈st,a^t≈at,r^t≈rt。如果模型假设对某个固定的 s 0 s_0 s0成立,我们有
![]()
这转化为MVE MSE的表达式(两边平方)
![]()
其中 ( f π ) H ν (f^\pi)^H\nu (fπ)Hν表示从 ν \nu ν中的状态开始执行策略 π \pi π H次所产生的前推测量(pushforward measure)。这个非正式的演示通过假设模型几乎是理想的,演示了MVE MSE与潜在评论家MSE的关系。 我们验证上面的非正式推理是否存在模型错误。
Theorem 3.1 (Model-Based Value Expansion Error).
定义 s t , a t , r t s_t,a_t,r_t st,at,rt是从 s 0 ∼ ν s_0\sim\nu s0∼ν开始,使用真实动态 f f f,在策略 π \pi π下获得的状态、动作和奖励。类似的, s ^ t , a ^ t , r ^ t \hat{s}_t,\hat{a}_t,\hat{r}_t s^t,a^t,r^t使用的是习得的动力学模型 f ^ \hat{f} f^。令奖励 r r r为 L r − L i p s c h i t z L_r-Lipschitz Lr−Lipschitz,值函数 V π V^\pi Vπ为 L V − L i p s c h i t z L_V-Lipschitz LV−Lipschitz, ϵ \epsilon ϵ是H-step rollout 模型风险的上界:
![]()
则:
![]()
其中 c 1 、 c 2 c_1、c_2 c1、c2在 L r 、 L V L_r、L_V Lr、LV中最多呈线性增长,且在γ<1时与H无关。为了表示简单,我们假定 M S E ( f π ) H ν ( V ^ ) ≥ ϵ 2 MSE_{(f^\pi)^H\nu}(\hat{V})\geq\epsilon^2 MSE(fπ)Hν(V^)≥ϵ2,但当批评者的表现超过模型时,也会出现类似的结果。
因此,改进原始critic M S E ν ( V ^ ) MSE_\nu(\hat{V}) MSEν(V^)的充分条件是小的 ϵ \epsilon ϵ以及 γ < 1 \gamma<1 γ<1,并且critic在想象状态上至少与从 ν \nu ν中采样的那些状态一样准确:
![]()
然而,如果 ν \nu ν是一个任意的抽样分布,例如由探索性策略产生的抽样分布,则等式(4)的不等式很少成立。特别是,这种幼稚的选择导致整体性能不佳(图3),并且抵消了基于模型的reward估计的好处,即使假设有一个完美的Oracle动态模型(图6)。因此,如果 V ^ \hat{V} V^在来自 ν \nu ν的bellman误差上训练,那么 ( f π ) H ν (f^\pi)^H\nu (fπ)Hν和 ν \nu ν之间的分布不匹配将抵消 γ 2 H \gamma^{2H} γ2H的好处。事实上,任何基于模型的方法,评估来自 ( f π ) H ν (f^\pi)^H\nu (fπ)Hν关于想象状态critic的 V ^ \hat{V} V^,都必须谨慎,不要只在真实分布 ν \nu ν上训练critic。我们相信,这种见解可以被纳入类似于MVE的各种工作中,例如价值预测网络(oh et al.,2017)。
我们提出了分布不匹配的一个解决方案。如果 ( f π ) H ν = ν (f^\pi)^H\nu=\nu (fπ)Hν=ν,即训练分布 ν \nu ν是 f π f^\pi fπ上的一个固定点,则问题消失。实践中,给定状态-动作对的任意off-policy分布 β \beta β,我们将 ν = E [ ( f π ) T β ] \nu=\mathbb{E}[(f^\pi)^T\beta] ν=E[(fπ)Tβ]设置为固定点的近似值,其中 T ∼ T\sim T∼ Uniform{ 0 , ⋯ , H − 1 0,\cdots,H-1 0,⋯,H−1}。如果我们接着对状态 s ^ T ∣ T ∼ ( f π ) T β \hat{s}_T|T\sim(f^\pi)^T\beta s^T∣T∼(fπ)Tβ进行采样,我们模型的精确性假设规定我们可以准确地模拟从 s ^ T \hat{s}_T s^T开始执行策略 π \pi π得到的状态 { s ^ T + i } i = 1 H − T \{\hat{s}_{T+i}\}_{i=1}^{H-T} {s^T+i}i=1H−T。这些模拟状态可用于精确构建k-step MVE目标 V ^ k ( s ^ T ) \hat{V}_k(\hat{s}_T) V^k(s^T),同时通过设置 k = H − T k = H-T k=H−T来遵守对模型的假设。然后可以使用这些目标在 ν \nu ν上训练 V ^ \hat{V} V^,而不仅仅在 β \beta β上。
由于我们无法访问 V ^ \hat{V} V^真正的MSE,因此我们最小化其关于 ν \nu ν的Bellman error作为替代。在这种情况下,使用目标 V ^ k ( s ^ T ) \hat{V}_k(\hat{s}_T) V^k(s^T)相当于用想象的TD-k error训练 V ^ \hat{V} V^。这种TD-k技巧使我们能够将分布不匹配问题限制在 ν \nu ν是近似固定点的程度。我们发现,与单独训练评论家相比,TD-k技巧大大提高了任务能力(图3)。
3.2 Deep Reinforcement Learning Implementation
在上一节中,我们提出了一种分析,它激发了我们基于模型的价值扩张方法。 在本节中,我们将介绍这种方法在高维连续深度强化学习中的实际实现。 我们演示了如何在一般的演员 - 评论家环境中应用MVE以改善目标Q值,目的是实现更快的收敛。 我们的实现依赖于参数化的actor π θ \pi_\theta πθ和critic Q φ Q_\varphi Qφ,但是请注意,如果计算 π ( s ) = arg max a Q φ ( s , a ) \pi(s)=\arg\max_aQ_\varphi(s,a) π(s)=argmaxaQφ(s,a)是可行的,则可以去除单独参数化的actor。
我们假设Actor-critic方法提供了一个可微的actor损失 l a c t o r l_{actor} lactor和一个critic损失 l c r i t i c π , Q l_{critic}^{\pi,Q} lcriticπ,Q。这些损失是 θ , φ \theta,\varphi θ,φ的函数以及从某些分布 D D D中采样的转换 τ = ( S , A , R , S ′ ) \tau=(S,A,R,S') τ=(S,A,R,S′)。例如,在DDPG中,根据确定性连续策略改进定理, E D [ l a c t o r ( θ , φ , τ ) ] = E D [ Q φ ( S , π θ ( S ) ) ] \mathbb{E}_D[l_{actor}(\theta,\varphi,\tau)]=\mathbb{E}_D[Q_\varphi(S,\pi_\theta(S))] ED[lactor(θ,φ,τ)]=ED[Qφ(S,πθ(S))]的梯度 θ \theta θ近似上升 J D J_D JD。DDPG critic的损失取决于目标actor π \pi π和critic Q:
![]()
MVE依赖于我们从转换 β \beta β的经验分布中得出的近似定点构造。回想一下上一节中我们的近似值,它依赖于当前的策略来想象最多H个步骤:
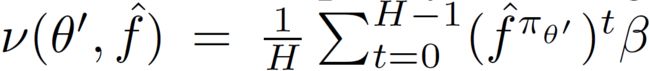
其中 f ^ π θ ′ ( τ ) = ( A ′ , S ′ , r ( S ′ , A ′ ) , f ^ ( S ′ , A ′ ) ) \hat{f}^{\pi_{\theta'}}(\tau)=(A',S',r(S',A'),\hat{f}(S',A')) f^πθ′(τ)=(A′,S′,r(S′,A′),f^(S′,A′))且 A ′ = π θ ′ ( S ′ ) A'=\pi_{\theta'}(S') A′=πθ′(S′)。因此,当从一个从 β \beta β中采样的状态开始时,从 ν \nu ν的采样转换等效于从任何点到H个想象步骤的采样。MVE增强方法遵循通常的actor-critic模板,但是critic训练使用MVE目标和从 ν \nu ν(Alg. 1)采样的转换(transitions)。
初始化四个网络的参数(Actor网络θ、Critic网络φ、Target Actor网络θ'、Target Critic网络φ')
初始化replay buffer β为∅
进入外循环
在真实环境中执行任意探索性策略
将观测到的转换(s,a,r,s')放入replay buffer β中
使用β中的数据训练动力学模型
进入内循环
从β中采样一个装态转换τ_0
使用π_θ,Q_φ,τ_0更新Actor网络参数θ
使用拟合的动力学模型与Target Actor网络π_{θ'},想象转换τ_1,τ_2,...,τ_{H-1}
对于所有k=H-t,定义\hat{Q}_k是Q_φ'的k-step MVE
使用π(θ'),τ_t,\hat{Q}_k按下式(ν-based Bellman error)更新Critic网络参数φ
每隔几次循环更新Target网络参数θ'和φ'
退出内循环
退出外循环
返回网络参数θ和φ
结束
我们假设目标actor的rollouts(其参数是以前迭代的指数加权平均值)与DDPG等价,后者使用目标actor计算目标value的估计值。取 H = 0 , ν ( θ ′ , f ^ ) = β H=0,\nu(\theta',\hat{f})=\beta H=0,ν(θ′,f^)=β,我们恢复了原始的actor-critic算法。我们的实现使用多层全连接神经网络来表示Q函数和策略。 我们使用DDPG描述的actor和critic损失。
重要的是,我们不使用想象缓冲区来保存模拟状态,而是通过从 ν ( θ ′ , f ^ ) \nu(\theta',\hat{f}) ν(θ′,f^)中采样来动态生成模拟状态。我们对 ν ( θ ′ , f ^ ) \nu(\theta',\hat{f}) ν(θ′,f^)进行分层抽样,对于第11行中的每一个 t ∈ { 0 , ⋯ , H − 1 } t\in\{0,\cdots,H-1\} t∈{0,⋯,H−1},一次取 H H H个相关(依赖)样本。首先,我们从 β \beta β中抽取一个真实的转换 τ 0 = ( s − 1 , a − 1 , r − 1 , s 0 ) \tau_0=(s_{-1},a_{-1},r_{-1},s_0) τ0=(s−1,a−1,r−1,s0),根据探索性策略从与环境的交互作用中观察到转换的经验分布。我们使用习得的动力学模型 f ^ \hat{f} f^去生成 s ^ t \hat{s}_t s^t和 r ^ t \hat{r}_t r^t。由于 π θ ′ \pi_{\theta'} πθ′在 θ , φ \theta,\varphi θ,φ联合优化过程中发生变化,这些模拟状态在批处理后立即被丢弃。然后我们采用随机 ▽ φ \triangledown_\varphi ▽φ步来最小化 Q φ Q_\varphi Qφ的 ν \nu ν-based Bellman error:

其中 Q φ ′ Q_{\varphi'} Qφ′和 a ^ t = π θ ′ ( s ^ t ) \hat{a}_t=\pi_{\theta'}(\hat{s}_t) a^t=πθ′(s^t)使用目标参数值(Alg. 1的11-13行)。因此,对贝尔曼误差的每一次观察都依赖于一些真实的数据。
对于动力学模型 f ^ \hat{f} f^,我们使用具有8层,每层有128个神经元,学习率固定为 1 0 − 3 10^{-3} 10−3的神经网络来预测real-vector-valued states间的差异。虽然我们期望一个更精确、更精心设计的模型能够允许我们使用更大的H,但即使是一个弱模型,在一个灵活类的所有任务中共享超参数,也足以证明我们的观点。
4. Results
我们希望在实验中验证如下几点:
- MVE是否改进了 Q π Q^\pi Qπ的估计;
- 改进的评估是否导致更快的掌握(收敛);
- TD-k技巧是否解决了分布不匹配问题。
4.1 Performance
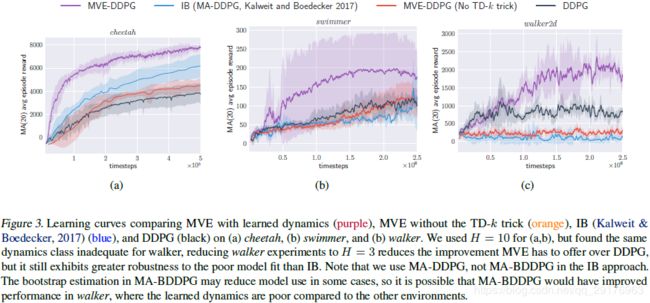
从图3可以看出,从一个学习模型中加入合成样本可以极大地改善无模型RL的性能,大大减少获得良好性能所需的样本数。仅当通过a short horizon和TD-k技巧仔细地结合该合成经验时才能获得这种改进。正如我们将在下一节讨论的那样,这里的具体设计决策对于获得良好结果至关重要,这有助于解释在先前工作中使用相关方法观察到的学习神经网络模型缺乏成功(Gu et al., 2016)。
MVE-DDPG通过处理从动力学模型获得的合成数据改进了类似的方法,例如MA-DDPG。这种替代方法将模拟数据添加回单独的想象缓冲区,有效地将 β β β从Alg. 1修改为 β β β与模拟数据之间的混合(其中混合物取决于从每个缓冲区取得的样本的相对数量)。这是有问题的,因为策略在训练期间发生变化,因此,从表示 π \pi π将采取的行动角度来看,来自真实和虚假数据混合分布的数据相对于 ν \nu ν来说是过时的。在我们的MA-DDPG实现中,我们不以这种方式重用想象状态,但MVE-DDPG仍然优于MA-DDPG。我们怀疑这是由于两个因素:(1)IB方法中虚构状态的过时性,以及(2)使用更多虚构数据和过度训练actor之间的微妙交互。为了使用额外的合成数据,IB方法必须对假想批次采取更多的梯度步。另一方面,由于MVE-DDPG使用实际和模拟数据上的平均梯度,因此选择额外的梯度步骤成为独立的考虑因素,这取决于所训练的actor-critic方法的稳定性。
4.2 MVE as Critic Improvement



为了验证TD-k技巧对正确训练 Q ^ \hat{Q} Q^十分重要,我们对cheetah环境进行了消融分析(ablation analysis):我们保持所有参数不变,并使用真实动力学模型 f f f代替学习的动力学模型 f ^ \hat{f} f^,使模型误差为零。如果 M S E β ( Q ^ ) ≈ M S E ( f π ) H β ( Q ^ ) MSE_\beta(\hat{Q})\approx MSE_{(f^\pi)^H\beta}(\hat{Q}) MSEβ(Q^)≈MSE(fπ)Hβ(Q^),即使没有TD-k技巧,MVE估计必须在H中呈指数级增长。 但事实并非如此。使用TD-k技巧,增加H,效益会增加但收益递减(图6)。 如果没有调整分布不匹配,超过某一点,增加H会伤害性能。因为动力学模型在这些情况下是理想的,唯一的区别是Critic Q ^ \hat{Q} Q^在状态 ν = 1 H ∑ t = 0 H − 1 ( f π ) t β \nu=\frac{1}{H}\sum_{t=0}^{H-1}(f^\pi)^t\beta ν=H1∑t=0H−1(fπ)tβ而不是 β β β的分布上训练,其中 β β β是由replay buffer产生的经验分布。由于td-k技巧增加了已训练的 Q ^ \hat{Q} Q^的训练数据的支持,Critic的函数类可能需要有足够的能力(深度)捕捉新的分布,但是我们在实验中没有发现这是一个问题。
5. Related works
关于将动力学模型引入到model-free RL和值估计的方法大概可分为三种:
- Direct incorporation of dynamics into the value gradient,;
- Use of imagination as additional training data;
- Use of imagination as context for value estimation。
最后,我们注意到MVE与n-step return方法高度相似。都使用了short horizon rollouts来改进估计的价值,在计算Bellman误差时经常将其作为目标值。通常,n-step return 方法是on-policy的:它们将一些状态-动作对的目标Q值估计为 ∑ t = 0 H − 1 γ t r t + γ H Q ^ ( S H , a H ) \sum_{t=0}^{H-1}\gamma^tr_t+\gamma^H\hat{Q}(S_H,a_H) ∑t=0H−1γtrt+γHQ^(SH,aH),用于观察到的H步轨迹中的奖励 r t r_t rt的轨迹(Peng&Williams,1994)。MVE与n-step return方法的主要区别在于通过动态建模进行显式状态预测,因为它可以通过使用off-policy数据实现更快的学习。
References
[1] https://zhuanlan.zhihu.com/p/72642285
