路由寻迹常见算法-启发式
路由寻迹之启发式搜索
启发式搜索是指我们在搜索路径时,首先选择最有希望的的节点去拓展,这种被称为启发式搜索.
启发函数
那么什么可以用来定义最有希望,如何来界定一个点比另外一个点、一个网格比另外一个网络更有希望,这就要通过启发函数来进行计算得到。
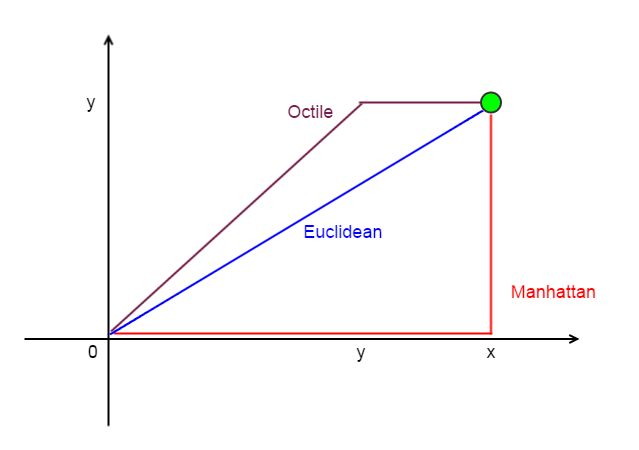
对于我们常见的网格图来说,我们规定只能上下左右来移动的话,那么通常来说都会使用曼哈顿距离来当做启发函数。
什么是曼哈顿距离
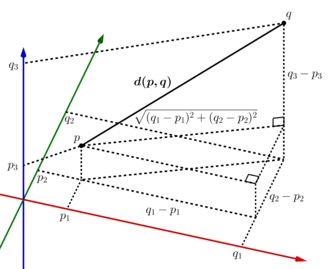
根据官方定义,曼哈顿距离——两点在南北方向上的距离加上在东西方向上的距离,即d(i,j)=|xi-xj. |+|yi-yj. 。 对于一个具有正南正北、正东正西方向规则布局的城镇街道,从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离,因此,曼哈顿距离又称为出租车距离。

function Manhattan(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
// 在最简单的情况下, D 可以取 1, 返回值即 dx + dy
return D * (dx + dy)
切比雪夫距离
数学上,切比雪夫距离(Chebyshev distance)或是L∞度量是向量空间中的一种度量,二个点之间的距离定义为其各座标数值差的最大值。 以(x1,y1)和(x2,y2)二点为例,其切比雪夫距离为max(|x2-x1. ,|y2-y1.

function Chebyshev(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
// max(dx, dy) 保证了斜对角的距离计算
return D * max(dx, dy)
欧式距离
function heuristic(node) =
dx = abs(node.x - goal.x)
dy = abs(node.y - goal.y)
// 在最简单的情况下, D 可以取 1, 返回值即 sqrt(dx * dx + dy * dy)
return D * sqrt(dx * dx + dy * dy)
启发函数总结
Dijkstra算法
Dijkstra算法是计算机大佬Dijktra在1956年提出的,是一个本质上位广度优先搜索的寻找最短路径算法。
其具体步骤是:
1、g(n): 从起始点到当前点 n 的开销, 在网格地图中一般就是步长.
2、将起始点 S 加入 open-list.
3、从当前的 open-list 中选取 g(n) 最优(最小)的节点 n, 加入 closed-list
4、遍历 n 的后继节点 ns
5、如果 ns 是新节点, 加入 open-list
6、如果 ns 已经在 open-list 中, 并且当前 h(ns) 更优, 则更新 ns 并修改 parent
7、迭代, 直到找打目标节点 D, 回溯得到路径
本质上来说,Dijkstra算法的效率其实一点都不高,时间复杂度为O(n2),但是它可以保证这个一定是全局的最短路径.
Best-First-Search
简称BFS,最佳优先搜索算法,其根据启发式函数的推断结果,跌打最优的节点,直到寻找到目标节点为止:
1、h(n) 代表从当前点 n 到目标点 S 的估算开销, 即启发函数.
2、将起始点 S 加入 open-list.
3、从当前的 open-list 中选取 h(n) 最优(最小)的节点 n, 加入 closed-list
4、遍历 n 的后继节点 ns
5、如果 ns 是新节点, 加入 open-list
6、如果 ns 已经在 open-list 中, 并且当前 h(ns) 更优, 则更新 ns 并修改 parent
7、迭代, 直到找打目标节点 D, 回溯得到路径
如果不使用open-list,则就会每次直接去寻找n次的后继节点最优节点,那么BFS算法就会退化为贪心最佳优先搜索算法
但是这种算法理论上只可以找到局部最优路径,虽然效率比DijkStra算法要高很多,但是最终的解不一定是最优解。
A-Star
A算法则是当前最流行、使用范围最为广泛的路径搜索算法,其融合了BFS和Dijkstra算法的长处,即兼顾了Dijkstra的精准性又获得了BFS的高效率。
1、f(n) = g(n) + h(n) , g(n) 和 h(n) 的定义同上
2、当 g(n) 退化为 0, 只计算 h(n) 时, A 即退化为 BFS.
3、当 h(n) 退化为 0, 只计算 g(n) 时, A* 即退化为 Dijkstra 算法.
4、将起始点 S 加入 open-list.
5、从当前的 open-list 中选取 f(n) 最优(最小)的节点 n, 加入 close-list
6、遍历 n 的后继节点 ns
7、如果 ns 是新节点, 加入 open-list
8、如果 ns 已经在 open-list 中, 并且当前 f(ns) 更优, 则更新 ns 并修改 parent
9、迭代, 直到找打目标节点 D.
A *算法在从起始点到目标点的过程中, *尝试平衡 g(n) 和 h(n), 目的是找到最小(最优)的 f(n).
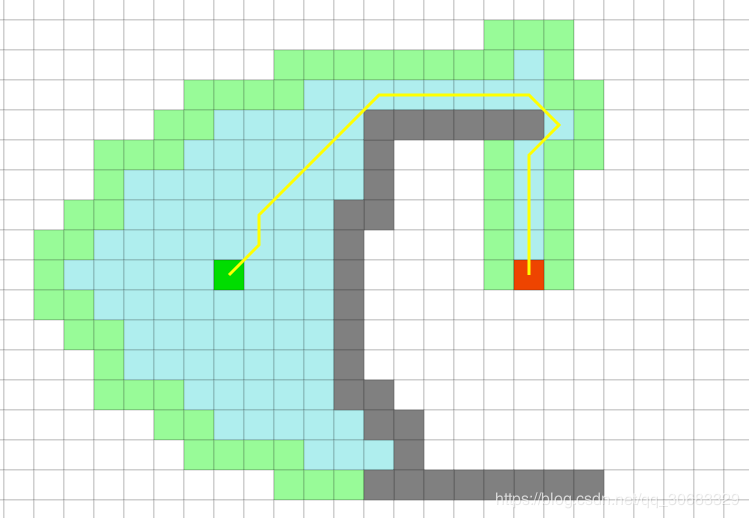
A-Star算法衍生算法
根据上面A-Star的算法,我们得知A-Star在每次选取下一节点时,都会有一个启发函数f(n) = g(n) + h(n)。g(n)表示已经走过的节点的信息 。h(n)代表还未行走的节点信息。
但是在每次迭代过程中,都会去除掉fn较低的节点,只会选取有限数量的后继节点,虽然这样提高了效率,但是却有可能丢失掉最优的路径。
本质上是一个集束搜索的思想。
动态加权A-Star
我们还可以对整个A-Star做一些优化和调整,比如说:
当距离起点越近, 快速前行更重要; 当距离目标点越近, 到达目标更重要. 基于这个原则, 可以引入权重因子, A 可以演进为选取 f(n) = g(n) + w(n) h(n) 最优的点, w(n) 表示在点 n 的权重. w(n) 随着当距离目标点越近而减小. 这是 动态加权 A (Dynamic Weighting A).
双向搜索A-Star
当从出发点和目标点同时开始做双向搜索, 可以利用并行计算能力, 更快的获得计算结果, 这是 **双向搜索 (Bidirectional Search). **此时, 向前搜索 f(n) = g(start, n) + h(n, goal), 向后搜索 f(m) = g(m, goal) + h(start, m), 所以双向搜索最终可以归结为选取 g(start, n) + h(m, n) + g(m, goal) 最优的一对点(m, n).、
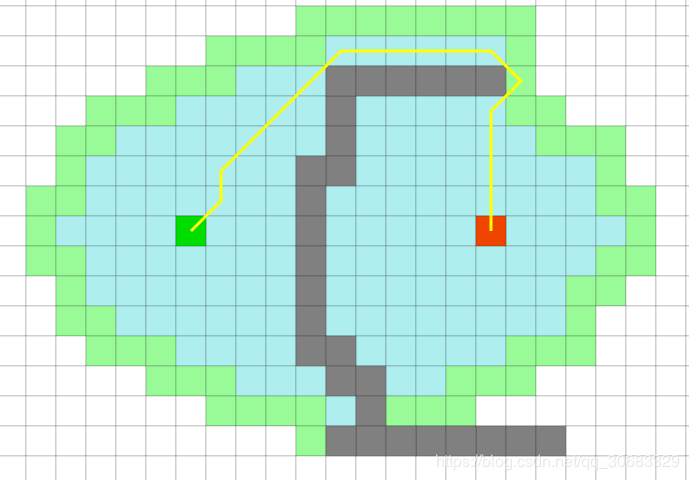
D-Star算法
A 在静态地图中表现很棒, 但是在动态环境中(例如随机的障碍物), 却不太合适, 一个基于 A 算法的 D 算法(D-Star, Dynamic A) 能很好的适应这样的动态环境. D 算法中, 没有 g(n), f(n) 退化为 h(n), 但是每一步 h(n) 的计算有所不同: *h(n) = h(n-1) + h(n-1, n), c(n-1, n) 表示节点 n-1 到节点 n 的开销.