LeetCode刷题记录2019/3/10
@LeetCode刷题记录2019/3/10
1. minimum-depth-of-binary-tree
Given a binary tree, find its minimum depth.The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
递归的思想:
分别计算左右两个节点的深度,采取较小的那一个加1,这里需要注意的是如果只有某一个子节点为空,则返回另一个非空节点的深度信息,而不是选择较小的深度加1.
class Solution {
public:
int run(TreeNode *root) {
if(root == NULL)
return 0;
int n_right;
int n_left;
n_right = run(root->right);
n_left = run(root->left);
if (n_right ==0||n_left==0)
return 1+n_left+n_right;
return n_left>n_right?(1+n_right):(1+n_left);
}
};
2.evaluate-reverse-polish-notation
Evaluate the value of an arithmetic expression in Reverse Polish Notation.
Valid operators are+,-,*,/. Each operand may be an integer or another expression.
Some examples:
[“2”, “1”, “+”, “3”, “*”] -> ((2 + 1) * 3) -> 9
[“4”, “13”, “5”, “/”, “+”] -> (4 + (13 / 5)) -> 6b
逆波兰表达式:遇到运算符,跳出前两个数进行运算,采用堆栈,后进先出
主要利用了stack,注意stack的top()和pop() 区别,注意建立的队列是int类型,还有pop 的第一个其实是第二个操作数,还有需要stoi(),转换数字。
class Solution {
public:
int evalRPN(vector &tokens) {
stack s;
int len=tokens.size();
for(int i=0;i 3.max-points-on-a-line
Given n points on a 2D plane, find the maximum number of points that lie on the same straight line.
思路:
利用的unordered_map
对于每一个点,求取出和其他点的直线和斜率,统计相同斜率的点,是一个双循环。
注意考虑 重复点以及斜率无穷的情况。(特别注意先求出非max中最大值再与ver比较,有可能某一次数据中只有ver点,这样map为空)
/**
* Definition for a point.
* struct Point {
* int x;
* int y;
* Point() : x(0), y(0) {}
* Point(int a, int b) : x(a), y(b) {}
* };
*/
class Solution {
public:
int maxPoints(vector &points) {
int len=points.size();
int ret=0;
for(int i=0;i < len;i++){
int dup=0;//重复点
int ver=0;//垂直点
int curmax=0;
unordered_map m;
for(int j = i+1;j < len;j++){
double x = points[i].x - points[j].x;
double y = points[i].y - points[j].y;
if(x == 0 && y == 0){
dup++;
}
else if( x==0){
ver++;
}
else{
m[y/x]++;
}
}
for( auto it = m.begin();it != m.end(); it++){//求出非MAX斜率中最大值
curmax=max(curmax,it->second);//注意max必须有一个是累计的前面的最大值
}
curmax=max(ver,curmax);//比较ver和非max斜率中的最大值
ret=max(ret,curmax+dup+1);
}
return ret;
}
};
4.sort-list
Sort a linked list in O(n log n) time using constant space complexity.
归并排序,归并排序分为两部分,一个部分是分,即不断的二分,一部分是治,merge的过程
1.寻找链表的中点,分配两个指针,一个快指针,一个慢指针,快指针间隔跳转,当快指针结尾时候,慢指针位于中点,然后通过指针的操作,将一个链表,从中间截断,这时不需要重新申请空间。只是地址调转
2.合并,将sort函数到达递归终点,跳出时,进行合并,注意需要考虑一边先行结束。
结构体的引用,如果是实体比如ListNode a(0),*p;则是a.next,p->next;
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *sortList(ListNode *head) {
if(!head || !head->next){
return head;
}
//find the middle
ListNode* slow=head, *fast=head->next;\\fast指向slow的下一个
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
}
ListNode* left=sortList(slow->next);
slow->next=NULL;
ListNode* right=sortList(head);
return merge(left,right);\\排序过程
}
ListNode *merge(ListNode *L,ListNode *R){
ListNode m(0),*p;
p=&m;
while(L && R){
if(L->val < R->val){
p->next=L;
p=L;
L=L->next;
}
else{
p->next=R;
p=R;
R=R->next;
}
}
if(L){p->next=L;}
else{p->next=R;}
return m.next;
}
};
5. insertion-sort-list
Sort a linked list using insertion sort
思路:建立另一个表节点,然后对原链表的每一个元素进行插入排序。寻找插入节点的时候,需要两个指针,一个存储插入节点的前一个指针地址,一个存储插入节点的后一个指针地址
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *insertionSortList(ListNode *head) {
if (!head)
return head;
ListNode tmp(0);
ListNode* p, *q, *t;
while (head) {
p = &tmp;//插入节点的前一个节点
q = p->next;//插入节点的后一个节点
t = head;
head = head->next;
while (q && q->val < t->val) {//找到原链表中t元素的值在临时列表中的位置
p = p->next;
q = q->next;
}
t->next = q;
p->next = t;
}
return tmp.next;
}
};
6.binary-tree-preorder-traversal
Given a binary tree, return the preorder traversal of its nodes’ values.
For example:
Given binary tree{1,#,2,3},
1
2
/
3
return[1,2,3].
Note: Recursive solution is trivial, could you do it iteratively?
思路:
1.利用递归的思路,还有vector的运用,先将根节点存入vector中,然后遍历左边节点和右边节点。
2.利用v.push_back()函数,想在递归中实现数据传递,应考虑将其变成函数参数!!!!!!
3.易错:注意vector的函数参数地址传递声明带&,void不接受返回
/**
* Definition for binary tree
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
void preoder(TreeNode *root,vector&v){
if(root){
v.push_back(root->val);
preoder(root->left,v);
preoder(root->right,v);
}
}
vector preorderTraversal(TreeNode *root) {
vector v;
preoder(root,v);
return v;
}
};
7. reorder-list
Given a singly linked list L: L 0→L 1→…→L n-1→L n,
reorder it to: L 0→L n →L 1→L n-1→L 2→L n-2→…
You must do this in-place without altering the nodes’ values.
For example,
Given{1,2,3,4}, reorder it to{1,4,2,3}.
思路:
找到中点 ,将后半部分压入栈中,后进先出。
1.利用了前面讲的快慢指针寻找中点,还有stack,的top()和pop()函数,将中点之后的数据压缩进去stack中,进行插入。
2.注意只有一个节点的情况,因为有可能会出现NULL->next的情况,出现错误提示
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
void reorderList(ListNode *head) {
//找到中间的节点,利用快慢指针
ListNode *fast,*slow,*mid;
stack v;
slow=head;fast=head->next;
if(!slow || !fast){return;}//这一行必不可少,考虑只有一个元素的时候,不能出现NULL->next
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
}
fast=slow->next;
slow->next=NULL;\\重要
slow=head;
while(fast){
v.push(fast);
fast=fast->next;
}
while(!v.empty())
{
mid=slow->next;
slow->next=v.top();
v.pop();
slow->next->next=mid;
slow=mid;
}
8.linked-list-cycle-ii
Given a linked list, return the node where the cycle begins. If there is no cycle, returnnull.
Follow up:
Can you solve it without using extra space?
思路:
假设有环,则快慢指针会相遇。
1.利用了快慢指针,两指针一定会相遇,因为两个指针在环里面的距离假设为d,不用担心快指针跳过了慢指针,因为他们两的速度差是1,所以她们俩在环上的距离总是每次减1,最后总能减到0 ,每隔一步,可以缩小一个距离,最终会为0,相遇。注意,在slow未走完一圈的时候,fast走一圈多的时候会有一次相遇。
2.主要如果一开始fast=head->next的话,则存在x=k-1,但是如果fast=head,则x=k。
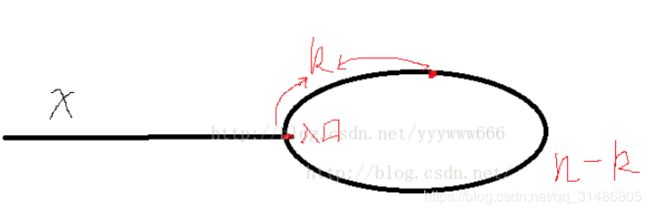
s=x+n-k;
f=x-1+2n-k;//注意f是从第二个节点开始的,也有的题目是从第一个节点开始的
f=2s;
x=k-1;
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast,*slow;
slow=head;fast=head->next;
while(!slow || !fast){ return NULL;}
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
if(slow == fast){
slow=head;
fast=fast->next;
while(slow != fast){
slow=slow->next;
fast=fast->next;
}
return slow;
}
}
return NULL;
}
};