相关滤波跟踪·MOSSE算法的梳理

相关滤波跟踪是当前目标检测与跟踪领域的一个研究热点，ICCV2010的这篇MOSSE算法可以说是入门必看，镇圈神作了。

一、目的：跟踪

一开始分不清跟踪和目标检测有什么不同，所以查了一些资料，以下只是我自己的理解：

区别于目标检测，跟踪最大的特点是处理的图像序列具有时效性（temporal data）。
跟踪的过程一般是在首帧进行目标识别（indentify）定位（locate），在后序的帧进行目标匹配（找到最相似的目标），再定位；目标检测方法是这个过程中的一种选择。此外，跟踪还有处理一些旋转、尺度变化等问题的功能，并具有一定的预判能力（比如：扫地机器人溜进桌子下面不见了，跟踪也能定位出一个大致的位置）。

不负责任地来说，检测是跟踪的基础，跟踪是高于检测的。

二、原理：相关滤波

接触相关滤波的时候我最容易搞混的地方就是各种空域 频域的转换，所以整理的时候我会特别把在空域还是频域特别标注出来。

2.1 滤波

滤波是一个图像处理，尤其图像增强时常用的方法（比如低通滤波器：把低频部分的信息保留，高频部分的信息滤掉）。很明显，滤波 是一个频域里的概念，但考虑到MOSSE的相关性从空域的角度比较好理解，因此需要暂时把频域滤波转换到空域滤波。

通过卷积模板，可以实现从频域到空域的转换，所以在空域中，滤波基本上通过一个矩阵模板（窗）来实现。简单讲，就是把滤波看做领域操作算子，利用 给定图像像素 周围像素的值 决定 此像素 最终的输出值。也就是说，输入图像与输出结果在像素上是一一对应的关系，滤波器只是一个操作算子。

2.2 相关

相关一开始是信号处理领域的一个概念，用来描述两个信号的相似程度。
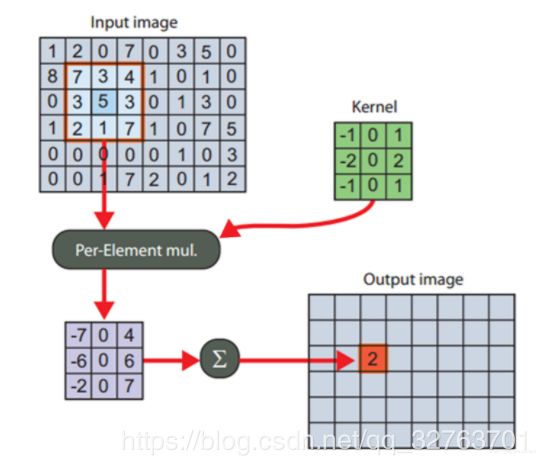
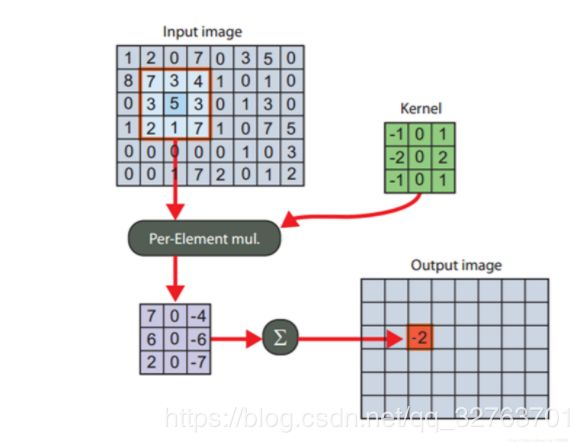
空域里的相关公式：

$$g=f⨂h$$

$$g(i,j)=\sum f(i+k,j+l)\cdot h(k,l)$$
(其中$f$是输入信号，$h$是相关核/滤波器，$g$是空域里的响应图。）

步骤：

  （1）滑动核，使其中心位于输入图像的$f(i,j)$像素上
  （2）利用上式求和，得到输出图像的$g(i,j)$像素值
  （3）充分上面操纵，直到求出输出图像的所有像素值

这里参考了(https://blog.csdn.net/qq_17783559/article/details/82254996)的解释。

很明显，输入信号与响应之间在像素值上是一一对应的，输入信号的信息与核越相似，响应值就越高。
因此，只要在下一帧里利用$h$找到响应值最高的位置就可以定位实现跟踪了，但问题在于：这样的方法计算太慢了。

考虑将空域的相关转化到频域提高运算速度。

三、算法：Minimum Output Sum of Squared Error (MOSSE) 滤波器

3.1 引入卷积算子

为了使空域的相关滤波转换到频域滤波以提高运算速度，引入卷积算子（注意：这里的卷积算子并没有什么实际的物理意义，可以看做一个把空域相关滤波转到频域的桥梁）。

卷积公式：

$$g=f\ast h$$

$$g(i,j)=\sum f(i-k,j-l)\cdot h(k,l)$$

很明显，相关运算是把$h$旋转了180°的卷积运算，所以$g=f⨂h=f\ast h^{\ast }$

通过卷积定理：函数卷积的傅立叶变换是函数傅立叶变换的乘积，上式可以变换为$FFT(g)=FFT(f)\cdot FFT(h^{\ast })$

表示为$$G=F\cdot H^{\ast }$$

但实际中很难通过$H^{\ast }=\frac{G}{F}$得到滤波器$H$

3.2 引入最小二乘法

最小二乘法是曲线拟合时的一种方法，通过最小化误差的平方来寻找数据的最佳函数配比。
在MOSSE中通过最小化实际输出的卷积和期望输出卷积之间的方差来得到合适的滤波器（minimizes the sum of squared error between the actual output of the convolution and the desired output of the convolution），即求解

$$\underset{H^{\ast }}{\min }\sum _i{\left|F_i\cdot H^{\ast }-G_i\right|}^2$$
(其中$i$ 表示第$i$个训练样本）

为了优化运算（element-wise），将上式转化为

${\min }_{H^{\ast }}{\sum }_i{\left|F_{i\omega \nu }\cdot H_{\omega \nu }^{\ast }-G_{i\omega \nu }\right|}^2$

(其中下标 表示第$i$ 个样本的$\omega$行$\nu$列）

${\min }_{H^{\ast }}{\sum }_i{\left|F_{i\omega \nu }\cdot H_{\omega \nu }^{\ast }-G_{i\omega \nu }\right|}^2$

$={\min }_{H^{\ast }}{\sum }_i\left[\left(F_{i\omega \nu }\cdot H_{\omega \nu }^{\ast }-G_{i\omega \nu }\right)\cdot {\left(F_{i\omega \nu }\cdot H_{\omega \nu }^{\ast }-G_{i\omega \nu }\right)}^{\ast }\right]$

$={\min }_{H^{\ast }}{\sum }_i\left[\left(F_{i\omega \nu }{H}_{\omega \nu }^{\ast }\right){\left(F_{i\omega \nu }{H}_{\omega \nu }^{\ast }\right)}^{\ast }-G_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{H}_{\omega \nu }-F_{i\omega \nu }{H}_{\omega \nu }^{\ast }{G}_{i\omega \nu }^{\ast }+G_{i\omega \nu }{G}_{i\omega \nu }^{\ast }\right]$

$={\min }_{H^{\ast }}{\sum }_i\left[F_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{\left(H_{\omega \nu }^{\ast }\right)}^2-G_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{H}_{\omega \nu }-F_{i\omega \nu }{H}_{\omega \nu }^{\ast }{G}_{i\omega \nu }^{\ast }+G_{i\omega \nu }{G}_{i\omega \nu }^{\ast }\right]$

求和号内是一个关于$H^{\ast }$的开口向上的一元二次函数，其一阶导数等于0的解即$H^{\ast }$的最小值。

$$\frac{\partial }{\partial H^{\ast }}\underset{H^{\ast }}{\min }\sum _i\left[F_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{\left(H_{\omega \nu }^{\ast }\right)}^2-G_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{H}_{\omega \nu }-F_{i\omega \nu }{H}_{\omega \nu }^{\ast }{G}_{i\omega \nu }^{\ast }+G_{i\omega \nu }{G}_{i\omega \nu }^{\ast }\right]=0$$

$$\sum _i\left[F_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{H}_{\omega \nu }-F_{i\omega \nu }{G}_{i\omega \nu }^{\ast }\right]=0$$

$$F_{i\omega \nu }{F}_{i\omega \nu }^{\ast }{H}_{\omega \nu }-F_{i\omega \nu }{G}_{i\omega \nu }^{\ast }=0$$

得到封闭解

$$H_{\omega \nu }=\frac{\sum F_{i\omega \nu }{G}_{i\omega \nu }^{\ast }}{\sum F_{i\omega \nu }{F}_{i\omega \nu }^{\ast }}$$

$$H=\frac{\sum F_i\odot G_i^{\ast }}{\sum F_i\odot F_i^{\ast }}$$

3.3 引入学习效率$\eta$

考虑到防止滤波器过拟合，使滤波器能够较快的适应旋转、遮挡、尺度变化等问题，引入一个学习效率（learning rate）的参量$\eta$表示不同时序的帧的权重，所以滤波器公式表示为：

$H_i=\frac{A_i}{B_i}$

$A_i=\eta G_i\odot F_i^{\ast }+(1-\eta )A_{i-1}$

$B_i=\eta F_i\odot F_i^{\ast }+(1-\eta )B_{i-1}$

学习效率参量使得时序离当前帧越近的帧所占权重越大，之前的帧的学习结果随时间呈指数递减。

四、流程：滤波器的初始化和在线更新

4.1 预处理

通常都会对特征提取的图像信息进行一些预处理：
（1）用log函数对像素值进行处理，降低对比度（contrasting lighting situation）。
（2）进行平均值为0，范数为1的归一化。
（3）用余弦窗口进行滤波，降低边缘的像素值。

4.2 流程图

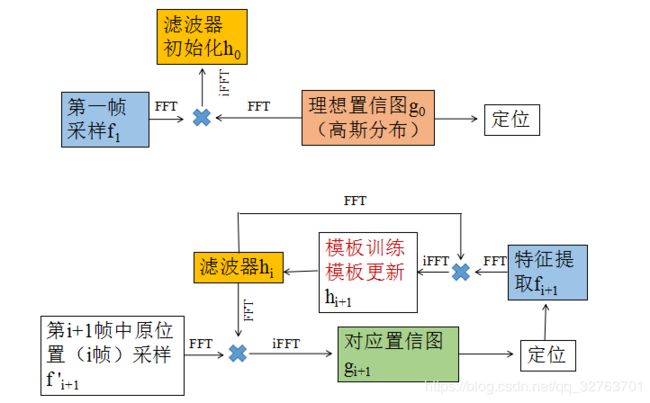
上半部分是滤波器初始化的过程，第一帧的特征提取$f_1$和高斯分布的理想置信图（相应）$g_{i+1}$已知，自然地，可以得到初始化的滤波器模板$h_0$,为了避免过拟合，对滤波器的初始化模板进行了一些处理。

下半部分是滤波器更新的过程，mosse算法的优越之处就在于滤波器模板能够利用定制的置信图$g_i$进行训练并在线更新，减少了目标丢失的可能性。

一次训练包含两次采样，第一次采样是在当前帧（$i+1$）中定位上一帧（$i$）目标位置进行采样，通过滤波器得到响应，为了便于理解，我暂时把这个响应称为过渡响应，它的傅里叶变换即回归模型中的$G_i$。

利用过渡响应得到当前帧中响应最大的像素定位，对当前帧进行第二次采样，此时，目标位于采样框中心。采样结果的傅里叶变换即模型中的$F_i$。

由此，模型中的输入值全部确定，${\min }_{H^{\ast }}{\sum }_i{\left|F_i\cdot H^{\ast }-G_i\right|}^2$

利用以上模型进行训练，得到新的滤波器$h_{i+1}$，对滤波器模板进行更新，进入下一帧。

以上，就是MOSSE算法的大致过程，欢迎讨论。(●’◡’●)

[分割线181105]
%修改了几个理解错误